基于可变步长的光谱响应曲线分形维计算方法研究

吕凤华,舒 宁,陶建斌,付 晶

(1.武汉大学遥感信息工程学院,武汉 430079;2.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079)

基于可变步长的光谱响应曲线分形维计算方法研究

吕凤华1,舒 宁1,陶建斌2,付 晶1

(1.武汉大学遥感信息工程学院,武汉 430079;2.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079)

提出了一种基于可变步长 (即基于不同采样率)的高光谱图像响应曲线分形维计算方法。该方法在不同的采样率下对光谱响应曲线进行采样,计算相邻点的光谱响应差值,统计采样点的差值总和,利用最小二乘法求出分形维。为了提高计算效率,运用多线程的技术将高光谱图像分成几个部分,各部分的分形维由多核计算机同时并行计算。实验结果表明,该方法能较好地改善量规法与网格法计算效率低、精度不高等问题,取得了良好的效果。

分形维;高光谱图像;改进分形维计算;多线程

0 引言

降维是高光谱遥感图像高维数据处理的关键技术,一般分为两种途径:一种是从众多的波段中挑选感兴趣的若干波段;另一种是通过某种数学方法对数据进行变换压缩,从而达到降维的目的[1]。分形是一种描述自然界中不规则和复杂现象的优秀数学方法,它将高光谱数据从高维空间映射到低维空间,提高了高光谱数据的处理效率[2]。分形也是高光谱遥感图像纹理特征提取的一种新方法,为高光谱遥感图像分类提供了重要的纹理信息。作为高光谱数据处理的新方法,分形维的计算有多种方法,例如,改变粗视化程度方法、由测度关系求取分形维的方法、根据相关函数求分形维的方法、由分布函数求分形维的方法以及根据波谱特征求分形维的方法[3]。其中,改变粗视化程度是求取曲线分形维的主要方法,此法又可分为网格法和量规法等[4]。网格法算法简单,易于实现,但精度不够高;量规法相比于网格法虽然在精度上有所提高,但算法复杂,同时光谱响应曲线分形维计算是基于响应曲线的统计自相似特征,由于光谱响应曲线数据量有限,再加上地物复杂和大气对光谱信号的影响,使得不同地物之间的分形维接近,分形维的精度并不是很高。在应用光谱响应曲线求取分形维的过程中,存在着数据量的大小与计算精度、计算效率相矛盾的问题,即数据量太小会影响地物之间分形维的可分性和精确度,而数据量太大又降低计算效率。

本文提出的基于可变步长的光谱响应曲线分形维计算方法,是在保持分形精度的前提下进行改进的。改进后的算法简单,易于实现,同时利用多线程技术进行并行计算,极大地提高了不同地物分形维间的差值和图像光谱响应曲线分形维的计算效率。

1 可变步长下高光谱图像分形维计算

1.1 算法的基本思想

由于高光谱响应曲线具有统计自相似性,因此根据分形的基本原理,有

式中,S(d)是在不同的采样率 (d)下,光谱响应曲线上相邻点响应值差值的总和;C是常数;D是分形维。

在实际计算过程中,S(d)=|f(xi+d)-f(xi)|,i=1,2,…,M ax(M ax是延拓的范围);|f(xi+d)-f(xi)|代表的是相邻点光谱值差的绝对值;d=2j,j=1,2,…,lb M ax。

对式 (1)两边取对数并化简,得到

式中,lb C为常数,令 b=lb C,k=D-2,则式

(2)可简化为

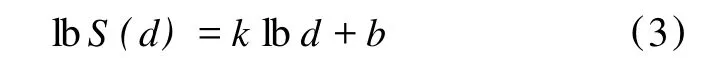
利用最小二乘法对统计值 S(d)和 d拟合出直线斜率 k,便可以得到分形维值。

1.2 算法流程

完整的算法流程如图 1所示。

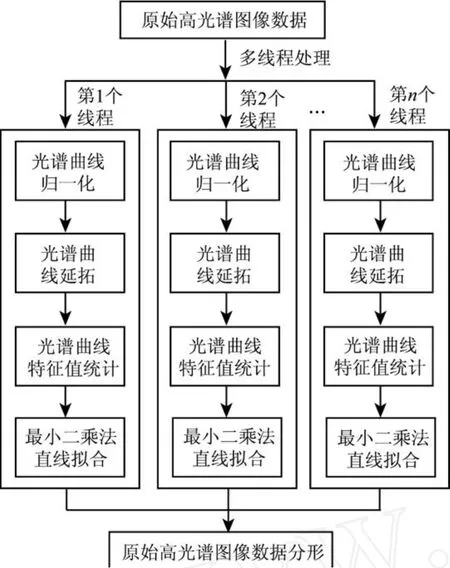
图 1 算法流程Fig.1 A lgor ithm flow char t

1.2.1 高光谱图像光谱响应曲线的预处理

本文分形维值计算是基于高光谱图像中每个像元的光谱响应曲线没有受到噪声影响的条件下进行的。光谱响应曲线的预处理包括如下 3部分:

(1)对光谱响应曲线数据进行多线程处理。根据创建的线程数目,将高光谱图像数据分为几块,每一个线程获得一个数据块。在计算过程中,每个线程同时并行处理各自获得的高光谱数据块。在多核计算机中,这种方式比一个线程更能够充分利用计算机资源,提高了 CPU的使用率,大大缩短了计算时间,有效地提高了计算效率。

(2)对光谱响应曲线数据进行归一化。归一化处理是为了使横纵坐标的量纲统一,使得光谱响应曲线上的光谱辐射值[0,255]映射到[0,1],即

式中,fi′为归一化后的数值;fi为光谱辐射值,i=1,2,…,n;n为波段总数。

(3)对光谱响应曲线数据进行延拓。本文提出的算法是统计相邻点的光谱响应差值,如果单纯使用原始数据,就会有如下缺憾:①统计的数值数量少,得不到精确且稳定的斜率值;②单纯利用原始数据,不能够统计到光谱响应曲线的细节部分,使结果之间的可分性较差;③本文的采样率是 2的整数次幂,原始数据可能不符合要求。因此,要对原始的光谱响应曲线进行 2的整数次幂的线性内插延拓。具体操作如下:

首先,确定插入点的总数M ax,其方法是取大于原始数据长度的整数,并且是 2的整数次幂;然后,按照式 (5)进行插入,即

式中,INT表示取整;ri为重采样后光谱响应曲线上的点值,i=1,2,…,M ax-1(M ax为重采样后光谱响应曲线上点的总数);f′为归一化后的数据。

1.2.2 可变步长下光谱响应曲线的特征值统计

传统网格法首先统计光谱响应曲线上最大值和最小值,然后将其差值除以网格的大小,从而得出覆盖这条曲线的网格数目。但是,在实际情况下,这种统计方式使得统计的网格偏大或偏小,结果与真实值之间存在差异。而量规法是在不同的测量尺度下,分别对光谱响应曲线进行测量,从而得到不同尺度下的光谱响应曲线长度。但是,在量规法中,涉及到大量复杂的三角函数和除法运算,如果尺度选择过小,则会影响计算效率;如果将尺度选择过大,就不能统计到光谱响应曲线的细节变化,造成了不同地物分形维之间差值的减小,影响了地物间的可分性。

本文提出的方法是在对光谱响应曲线进行延拓后,在不同采样率下统计光谱响应曲线相邻点响应值之差。在小的采样率下,可以统计到光谱响应曲线的细节变化,同时避免了大量的三角函数运算,提高了计算效率,并且能够精细准确地描述出光谱响应曲线的特征。

1.2.3 最小二乘法直线拟合

首先利用最小二乘法对统计数据进行直线拟合,求得直线斜率;然后,根据式 (2)、(3)求得分形维值,其结果如图 2所示。

图 2 4种不同地物的最小二乘法拟合直线Fig.2 The least squares fitting line of four different features

2 实验结果与分析

2.1 实验数据

为了验证算法的效果,选用江苏宜兴地区 OM IS高光谱数据,图像的空间分辨率为 4m,图像大小为400像元 ×400像元,该高光谱数据包括从可见光到红外 (近红外、中红外和远红外)共 128个波段。本文选取其中的 108个波段数据,舍弃一些噪声影响大的波段。

2.2 算法效果分析

在高光谱图像上分别从道路、居民地及农田等3种地物中选择 8个样本,并用量规法、网格法和本文提出的改进算法进行分形维值的计算 (表 1)。

表 1 不同地物之间样本的分形维值Tab.1 Different fractal dimensions of different features

图 3是由 3种算法得出的分形维特征图像。

图 3 3种算法的分形维特征图像Fig.3 The fractal dimensional images of three algorithms

从表 1可以得出,每类样本地物的分形维值只在一定的范围内变化,且各种地物的分形维值之间有一定的差值。虽然这种差值体现在小数点的后两位,但也可以通过数学手段将其映射到 0～255之间,得到一幅灰度图像,从而获得高光谱图像的纹理信息。但是,由于噪声因素的影响,一些样本地物的分形维值偏大或者偏小,造成类内分形维变化范围偏大。

曲线的分形维范围介于 1～2之间,且不同地物之间的分形维比较接近。由于受噪声等因素的影响,不同地物分形维发生了交叉,例如,网格法要求在不同尺度下统计光谱曲线覆盖的盒子,但是在计算过程中存在着“空盒子”的现象,从而造成了统计结果偏大。如在图 3的步长法特征图像上,建筑物的边缘和道路出现一些黑色点的现象;网格法特征图像上的道路、建筑物和农田的对比度低的现象。改进后的算法在一定程度上增大了不同地物分形维之间的差值,提高了地物分形维的精度,改善了网格法和步长法出现的问题,但是仍然存在着一些交叉现象,这是本文算法所未能彻底解决的一个问题。

本文分别采用量规法、网格法、单一线程改进算法及多线程改进算法对 100像元 ×100像元、200像元 ×200像元和 400像元 ×400像元的 OM IS高光谱图像进行分形维计算,并分别统计计算时间,其结果如图 4所示。

图 4 不同算法运算时间柱状图Fig.4 The Computing time histogram of different algorithms

从图 4可以看出,运算用时最长的是量规法,因为量规法在运算过程中涉及到大量的三角函数计算和除法计算,增加了计算时间;与量规法相比,网格法在计算时效性上有了少许提高;单一线程改进后的算法与量规法、网格法相比,所花费的时间大大减少,在运算的时效性方面有了很大提高;基于多线程技术的改进算法,在计算效率上比单一线程提高了近一倍的速率。可见,多线程技术在提高运算效率方面有着巨大的优势。但需指出的是,多线程技术运行的环境是有多处理器的计算环境,对于单处理器的环境,其运算时间与单线程算法相同。因此,在多核环境下,运算时间与线程的数目成反比关系。

3 结论

(1)针对像元光谱响应曲线分形特征提出的改进步长分形维计算方法能够有效提高不同地物分形维的精度,解决了分形维特征图中出现的对比度低和暗点问题,为高光谱遥感图像的分类研究提供了更为精确的纹理数据。

(2)在多核计算机环境下,多线程改进算法与传统的量规法和网格法相比,计算效率有了很大提高。

(3)提出的算法能较好地改善传统分形维算法中分形维精度不高和计算效率低的问题。实验结果表明,该算法在提高地物分形维精度和计算效率方面具有很大的潜力。

(4)尽管本文算法对像元光谱响应曲线的分形维计算取得了较好的效果,但是,大气因素、传感器本身的原因和噪声,影响了地物分形维的计算精度,出现了“同物异维”和“异物同维”的现象。因此,光谱响应曲线分形维算法的抗噪性和精确性是一个值得研究的课题。

[1] 张良培,张立福.高光谱遥感 [M].武汉:武汉大学出版社,2005.

[2] 苏俊英.分形测度在高光谱遥感影像中的应用方法研究[D].武汉:武汉大学,2008.

[3] 李水根,吴纪桃.分形与小波[M].北京:科学出版社,2002.

[4] 王 桥,吴纪桃.地图上曲线长度归算的分形方法研究[J].武测科技,1996,3:5-7.

[5] 姜志强.分形理论应用研究若干问题及现状与前景分析[J].吉林大学学报,2004,22(1):57-61.

[6] 杜华强,赵宪文,范文义.分形维数作为高光谱遥感数据波段选择的一个指标[J].遥感技术与应用,2004,19(1):5-9.

[7] 周子勇,李朝阳.高光谱遥感数据光谱曲线分形特征研究[J].中北大学学报,2005,26(6):451-454.

[8] 舒 宁,苏俊英.高光谱影像光谱响应曲线分维计算[J].遥感应用,2009,1:23-26.

[9] 连石柱.曲线分形维数的数值分析方法及应用[J].计算机工程与设计,1998,19(1):35-41.

[10]张季如,朱瑞赓,祝文化.用粒径的数量分布表征的土壤分形特征[J].水利学报,2004,25(4):1-7.

[11]舒 宁.卫星遥感影像纹理分析与分形分维方法[J].武汉测绘科技大学学报,1998,23(4):370-373.

[12]Tzeng Y C,Fan K T,Su Y J,et al.A Parallel Differential Box Counting Algorithm Applied to Hyeperspectral Image Classifications[J].IEEE Geo Science and Remote Sensing Letters,2009,5:216-219.

[13]Charles R T,Timothy RM,David JG.Suboptimal Minimum Cluster Volume Cover-Based Method for Measuring Fractal Dimension[J].IEEE Transactions on Geoscience and Remote Sensing,2003,25(1):32-41.

[14]Samia H.Measure of the Long-Range Persistence of Solar Irradiance Signals Using The Fractal Dimension[C]∥IEEE Internal Conference on Signal Processing and its Applications,2007:1-4.

[15]Georgia E P,Periklis K,Damianos S,et al.Comparison of Fractal Dimension Estimation Algorithms for Epilep tic Seizure Onset Detection[C]//IEEE International Conference on Bioinformatics and Bio Engineering,2008:1-6.

(责任编辑:刁淑娟)

Variable Step Size-Based Estimation of Fractal Dimension for Spectral Response Curve

LV Feng-hua1,SHU Ning1,TAO Jian-bin2,FU Jing1
(1.School of Remote Sensing and Information Engineering,Wuhan University,Wuhan 430079,China;2.State Key Laboratory of Information Engineering in Surveying,Mapping,and Remote Sensing,Wuhan University,Wuhan 430079,China)

This paper proposes an algorithm based on the variable step estimation of fractal dimension for spectral response curve of hyperspectral image.The algorithm carries out sampling on the spectral response curve at different sampling rates,computes the differential value between two consecutive points,and then counts the total sum of differential values about these sampling points. Finally,the fractal dimension is calculated by using the least squares method.To imp rove computation efficiency,the algorithm divides the hyperspectral image into several parts by using the multi-thread technology and then estimates the fractal dimension by the parallel computation of the polynuclear computer.Experimental results indicate that the algorithm is effective in that it solves the problem of computational inefficiency,low-fidelity,and weak separability in the algorithm of grid and step.

Fractal dimension;Hyperspectral image;Estimation algorithm of fractal dimension;Multi-thread

吕凤华 (1985-),硕士研究生,现主要从事遥感影像分析与应用研究。

TP 75

A

1001-070X(2011)01-0037-05

2010-05-31;

2010-07-26

国家 973项目“对地观测数据 -空间信息 -地学知识的转化机理”(编号:2006CB701303)资助。