数学形态学在配电网故障选线中的应用

2011-09-19邵如平

自动化仪表 2011年8期

徐骏邵如平时丹

(南京工业大学自动化与电气工程学院，江苏南京 210009)

0 引言

我国6～66 kV配电网大多采用小电流接地系统。实际现场运行中，单相接地故障约占总故障次数的80%，而小电流接地系统发生单相接地时，因线电压仍然对称、故障电流小，故不影响其对负荷供电，不必立即跳闸，规程规定系统可以继续运行1～2 h。但是随着配电网的发展，长时间运行易使故障扩大成两点或多点接地故障，弧光接地还会引起系统过电压，进而损坏设备和破坏系统的安全运行[1]。因此，快速而准确地选定故障线路对电力系统的安全可靠具有很重要的现实意义。

由于故障边界复杂随机多变、故障稳态分量较小，且易受系统运行方式改变、现场环境的干扰等的影响，配电网单相接地故障选线一直未能得到很好的解决。虽然目前已有多种选线算法[2－4]，但是这些方法都有各自的缺陷。本文对文献[5]所提出的基于数学形态学的单相接地故障暂态选线算法作了改进，采用多个结构元素取代单一结构元素进行形态滤波预处理，从而提高了抗干扰能力。

1 数学形态学理论

1.1 基本运算

数学形态学用集合描述目标信号[5－7]。在考察信号时，需要设计一种收集信号的“探针”，称为结构元素。通过在信号中不断移动结构元素，便可以提取有用的信息作为特征分析和描述。

在形态学中，膨胀和腐蚀是两个最基本的运算，而开运算、闭运算、开闭运算的级联等都是由这两种运算推导出的。

假设待处理信号f(n)是采样得到的一维多值信号，其定义域为Df={0，1，2，3，…，N －1};g(n)为一维结构元素序列，其定义域为Dg={0，1，2，3，…，M－1}。其中M和N都为整数，M ＜N。则信号f关于g的膨胀和腐蚀分别定义为[8－9]：

式中：⊕表示膨胀运算;Θ表示腐蚀运算。腐蚀和膨胀是不可逆运算。由灰度膨胀和腐蚀运算可以得到灰度开运算和闭运算，分别定义为：

以上两式中，○和·分别指形态开运算、闭运算。形态开闭运算可以理解为基本的滚球变换。“球”的形状由结构元素确定。对于电力系统中的一维信号来说，开运算主要是平滑并抑制信号正脉冲噪声，闭运算则抑制信号负脉冲噪声。采用开闭运算的级联组合形式，形态开闭(OC)和闭开(CO)分别定义为：

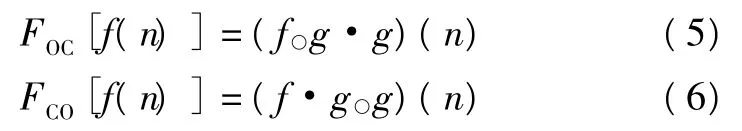
1.2 结构元素

在数学形态学的运算中，结构元素的作用类似于信号处理时的“滤波窗口”。常用的结构元素有直线、斜线、曲线、三角形和圆形等。依据理论分析和波形仿真发现，最优结构元素的选取与干扰的类型和频率、待处理数据序列的采样率、滤波后要保持的信号形状等因素密切相关。考虑小电流接地系统故障信号的特点、滤除尖脉冲、降低白噪声以及简化程序的需要，一般选取的是扁平形或半正弦型结构元素。

2 两结构元素并行复合形态滤波器

2.1 新型滤波器的构成原理

文献[5]通过分析比较，选用单一的扁平型结构元素构建成组合形态滤波器，从而实现对原始电气量进行滤波预处理。虽然这种形态开闭和闭开滤波器的组合可以抑制信号中的正负脉冲噪声，但是因为电力系统故障信号中含有多种类型噪声和漂移，而且各种干扰成分在结构上存在差异，所以仅采用一种结构元素滤波效果不太好。设计过程中，可以采用变结构元素的策略，即采用多个结构元素分别对信号形态进行运算，然后再将运算后的信号进行结合处理。本文提出了一种两结构元素并行复合形态滤波器，不仅可以有效地抑制多种噪声，而且可以保持更多有效的信息。

设输入信号f(n)由原始信号x(n)、脉冲噪声S1(n)和白噪声S2(n)组成，即：

定义多结构元素集为{g1(m1)，g2(m2)}、开闭最大滤波器和闭开最小滤波器为：

式中：OCg1=(f○g1·g1)(n);OCg2=(f○g2·g2)(n)、COg1=(f·g1○g1)(n);COg2=(f·g2○g2)(n)。

新型滤波器结构图如图1所示。

图1 新型滤波器结构图Fig.1 Structural diagram of the new morphology filter

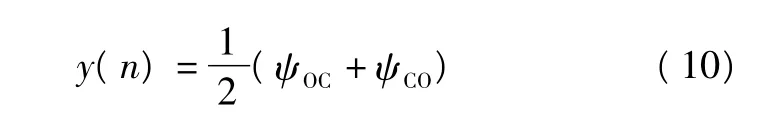
2.2 新型滤波器的滤波处理

由于现场环境的复杂性，小电流接地选线装置采集的电信号不可避免包含脉冲噪声和白噪声。因此，必须在选线前进行滤波处理。本文采用数学形态学算子进行突变量检测，所以不宜采用平滑能力较强的结构元素[10]。

为了消除尖脉冲、白噪声等其他噪声，两结构元素并行(SE)的类型、长度及幅值大小的选择尤为重要。通过选择不同的SE以及相同SE的不同长度、不同元素数值进行多次试验，在每周期采样200点的情况下，本文选用长度为6、幅值为2的扁平结构元素g1和长度为13、最大值为2的半正弦型结构元素g2相组合构成两结构元素并行复合形态滤波器来滤波。对原始零序电流去噪结果对比图如图2所示。

两结构元素并行复合形态滤波器的输出信号y(n)的表达式为：

图2 去噪结果对比图Fig.2 Comparison of the de-noising results

从图2(a)可以看出，文献[5]中采用单一的扁平结构元素形成组合形态滤波器，它在0.04 s以后的波形毛刺很明显，滤波效果不是很好;从图2(b)可以看出，两结构元素并行复合形态滤波器抗干扰性能强，滤波效果很好，具有明显的优势。

3 形态学突变量检测

3.1 选线判据

由文献[5]可知，为同时检测峰值点和谷值点，可以将 Top-Hat算子 Ot－h和 Bottom-Hat算子 Ob－h两个算子结合起来，构成峰谷检测器。峰谷检测器定义为：

De(n)可以对故障后的暂态信息进行突变量检测，确定突变明显点的突变方向和强度。经过形态学变换后，通过极性和幅值比较相结合的方法来判断出故障线路;然后根据故障线路的突变强度最大以及与其他线路的突变方向相反的原则确定故障线路。突变量检测的过程充分体现了单相接地故障的暂态过程的特点，而且利用De(n)进行突变量检测，计算简便，比单纯利用形态学梯度进行突变量检测抗干扰性强。具体选线流程如图3所示。

图3 选线流程图Fig.3 Line selection flowchart

基于数学形态学的故障选线算法主要步骤如下。

①检测母线的零序电压是否超过启动门槛，如果超过，则发出报警信号并启动选线保护装置，采集各条线路的零序电流进入步骤②;否则继续检测。

②利用两结构元素并行复合形态滤波器对零序电流进行滤波预处理，然后再利用形态学算子进行突变量检测。

③根据突变量检测结果进行故障判断：以突变极性优先为原则，如果突变明显点的突变极性均相同，则判断为母线故障;如果突变极性不相同，则通过幅值和极性综合比较进行判断，幅值最大且极性与其他线路相反的线路为故障线路，否则为非故障线路。

3.2 故障选线判定原则

故障选线判定主要有以下几条原则：①暂态判定原则，即要求具有一定强度的暂态零序电流用于故障选线;②排除短线路干扰的原则，短线路暂态零序电流幅值小且受电流互感器不平衡电流的影响较大，往往会造成选线错误，另外短线路暂态零序电流频率较高，突变强度较大，会对基于形态学算子的选线准确性造成影响，选线前一定要排除短线路对选线的干扰;③极性判断优先原则，故障线路的突变强度一般是最大的，由于现场环境太复杂，可能会导致故障线路突变点处的突变强度没健全线路大，但是突变的方向肯定相反，用极性判断优先原则还可以判断母线故障。

4 仿真及结果分析

4.1 系统仿真模型

系统仿真模型如图4所示。

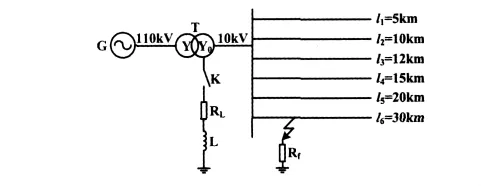
图4 系统仿真模型Fig.4 Simulation model

系统是一个有6条线路组成的110 kV/10 kV变电所，G为无限大电源，T为主变压器，消弧线圈电感串联电阻经隔离开关K投切。在EMTP仿真中，采用分布参数型等值电路。线路的正序参数为：R1=0.17 Ω，L1=0.38 mH，C1=9.69 nF;零序参数为：R0=0.23 Ω，L0=1.72 mH，C0=6 nF;线路长度消弧线圈参数为：补偿度为8%，电感 L=5.67 H，电阻RL=178.04 Ω;负荷采用三角型负荷，等效负荷阻抗Z=400+j20 Ω。

4.2 仿真结果及分析

系统故障点选取在l6的1/3处，在0.012 s时刻发生金属性单相接地，母线零序电压和各条线路零序电流波形如图5所示。

图5 电压和电流波形Fig.5 Waveforms of voltage and currents

从零序电压可以看出发生单相接地的暂态突变过程，从零序电流波形可以看出故障线路的电流幅值最大且方向和非故障线路相反。

利用形态学算子对经形态滤波后的各条线路零序电流进行突变量检测，分析波形数据发现各条线路均在第123、124、125三个点突变最明显，线路的突变量检测结果如表1所示。

表1 突变量检测结果Tab.1 Results of transient detection

从表1可以看出，线路l6突变强度最大，而且其突变极性与其他所有线路相反，得出线路l6为故障线路，验证了该算法的可行性。经过Matlab数据分析得出，每周期采样点数增加，突变点明显，但数值较小;每周期采样点数减少，突变点不明显，但数值较大，更接近零序电流波形。实际过程中，一般选择采样点数大于100，即可满足预期效果，而本文选择采集四个周期数据，每周期采样点数设为200。

除了上述的金属性接地故障外，笔者还通过改变故障时刻、过渡电阻大小、线路模型参数以及接地方式进行大量仿真和验算。结果表明，只要故障时暂态电流强度达到一定数值，就可以实现正确选线。实际应用时往往与其他稳态选线算法相结合，形成互补判据，从而实现可靠选线。

该暂态选线算法与小波变换算法相比，前者对信号的操作在纯时域内进行，不会使信号产生相位偏移和幅值衰减;同时，该算法只涉及加、减和取极值运算，不需要大量的乘法运算，故运算量很少、速度快、硬件消耗小;而且该算法对采样点数要求不高，不需要很高的采样频率。因此，该暂态选线算法和小波变换算法相比具有明显的优势。