广义RCS及近场电磁散射建模应用
2011-09-18梁子长王晓冰
梁子长,岳 慧,王晓冰,蔡 昆
(环境电磁特征国家重点实验室,上海 200438)
0 引言
RCS定义中隐含了观测距离趋于无穷大、入射电磁波为均匀平面波的假定条件[1~3]。一般,常根据被观测目标区域内入射电磁波等相位面符合平面条件与否,近似地将R=2D2/λ作为近场散射与远场散射的划分界线。此处:R为观测距离;D为被观测目标最大尺寸;λ为入射电磁波波长。上述假定条件定义的RCS也被视为远场RCS。在近场散射条件下,被观测目标区域内的入射电磁波等相位面为非平面,同时其在等相位面上的电场幅值也趋于非均匀分布。长期以来对近场RCS定义进行大量研究,但仍存在较大争议[4~10]。文献[4~6]在近场RCS定义中引入了天线方向图,认为其与观测天线相关;文献[7~9]认为近场RCS是远场RCS定义在均匀球面波入射条件下的推广。可见这些定义存在不确定性或难以完整描述近场电磁散射,需作进一步研究。另外,测试结果表明近场局部照射时,根据这些定义采用的天线方向图等效近似的近场电磁散射模型存在较大误差,也需深入研究。
为此,本文根据电磁场叠加原理,给出了一种与观测天线无关的广义RCS定义,引入对称极化等多种极化散射特征量,计算了近距离观测时金属平板目标的极化RCS曲线;同时根据广义RCS的定义,在近场电磁散射建模中进行照射场分解及接收合成,提出了一种有效的近场电磁散射建模方法,比较了方向图等效近似和场分解合成两种方法计算的金属平板目标的近场散射结果。
1 广义RCS
1.1 定义
根据电磁场叠加原理,入射电磁场均可分解为无限小理想电或磁偶极子辐射场的组合。若将理想偶极子作为照射及接收的观测条件,则广义RCS可定义为

式中:Ri,Rs分别为照射偶极子和接收偶极子与目标中心的距离;k为电磁波波数,且k=2π/λ;l为与目标散射特性、偶极子类型及指向有关的散射复函数;j为虚数;下标u,v=e,m表示照射及接收偶极子电或磁类型。若入射电磁波为理想电偶极子辐射的非均匀球面波,则

若入射电磁波为理想磁偶极子辐射的非均匀球面波,则
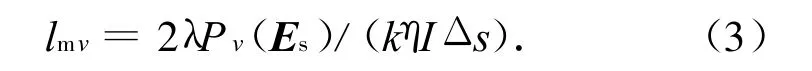
式中:η为自由空间的波阻抗;I d l,IΔs分别为照射电和磁偶极子的强度;Rv(Es),Ρv(Es)分别为单位强度的接收电或磁偶极子对散射电场的作用函数。在以偶极子中心为原点、指向为Z轴的坐标系中,当目标处于偶极子天线辐射区(Rs≫λ)时,Ρv(Es)可分别写为


式中:Es(γ,φ)为从(γ,φ)方向传播至接收偶极子的散射电磁波电场矢量;γ,φ分别为散射电磁波传播方向的俯仰角和方位角;eγ,eφ为对应球坐标单位矢量。
同时,在以被观测目标中心为原点的球坐标系中,处于位置(r,θ,φ)处的任意指向偶极子均可分解为eθ,eφ,er指向的同类型偶极子组合,因此为满足广义RCS描述散射特性的完整性,照射或接收偶极子将分别有6种类型:电偶极子的垂直、水平和对称极化(对应eθ,eφ,er指向的电偶极子)及磁偶极子的垂直、水平和对称极化(对应eφ,eθ,er指向的磁偶极子),对应的广义RCS将有6×6=36种极化组合,分别记为σuvpq。此处:下标p,q=V,H,S。其中:V,H,S分别表示照射及接收偶极子的垂直、水平和对称三种正交指向。广义RCS与远场RCS见表1。
可见,式(1~5)定义的广义RCS既能适于天线辐射区不同观测距离的电磁散射,又可与观测天线去相关,且当观测距离趋于无穷远时,广义RCS与远场RCS趋于一致:广义垂直或水平极化RCS将与对应的远场RCS趋于一致;广义对称极化RCS趋于零。同时在远距离处,当入射或接收为对称极化或两者均为对称极化时,(Ri)2σuvSq,(Rs)2σuvpS或(Ri)2(Rs)2σuvSS将与观测距离无关,因此也可将其作为目标电磁散射特征量进行研究。
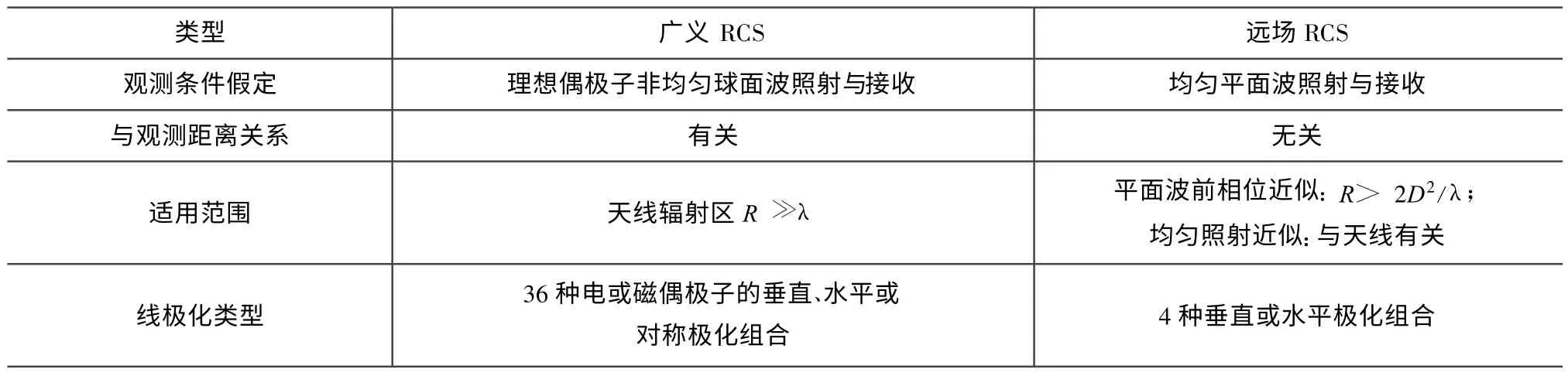
表1 广义和远场RCSTab.1 Generalized RCSand far-field RCS
1.2 金属平板散射计算结果
根据上述定义,对某金属平板的广义RCS进行了仿真计算。设金属平板长2 m,宽0.2 m,厚0.006 m,λ=8 GHz,R=3 m,采用PO、ILDC等高频法近似计算其后向散射,电及磁偶极类型的垂直、水平和对称等多种极化的广义RCS结果如图1~4所示。其中:金属平板位于yz面内,观测点位于xy面内。
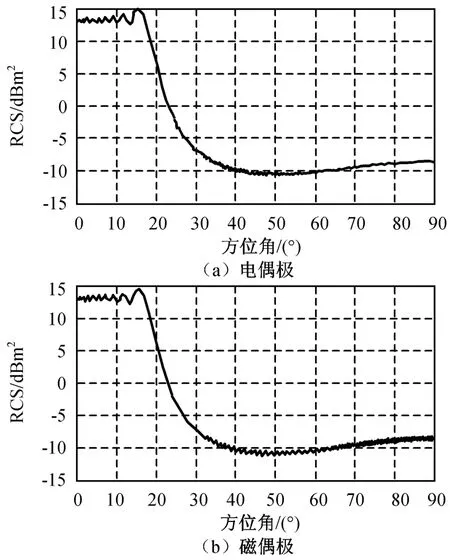
图1 金属平板目标垂直同极化的后向广义RCSFig.1 Backscattering generalized RCS of metal slab with co-vertical polarization
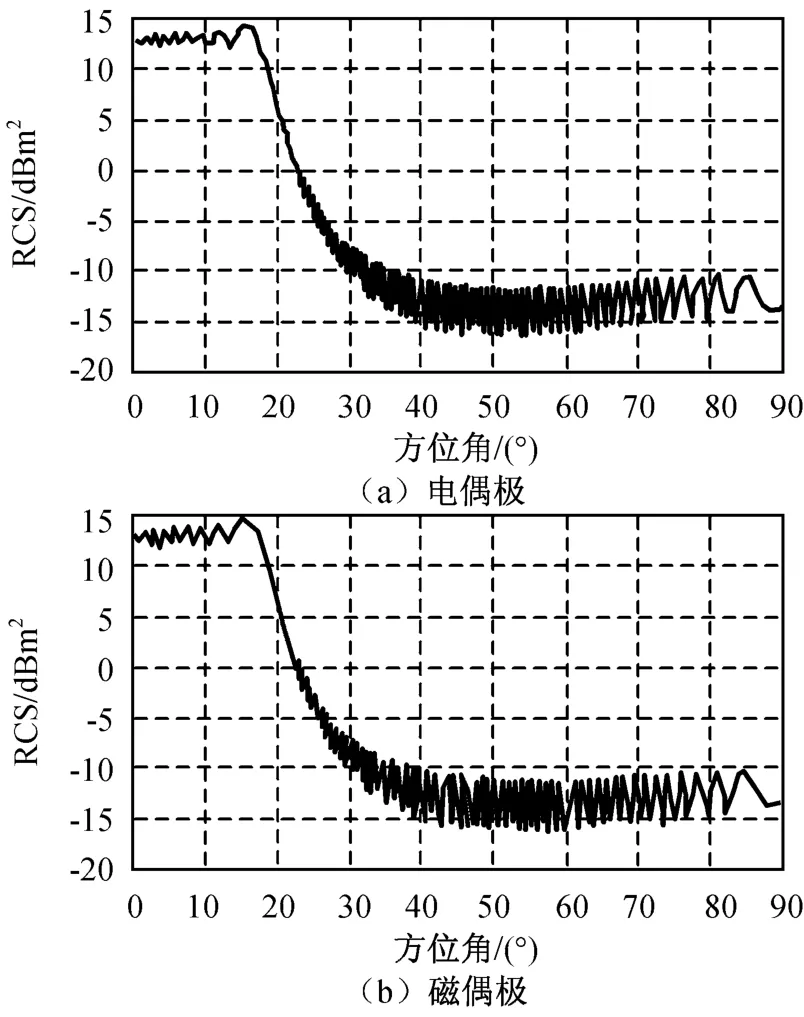
图2 金属平板目标水平同极化的后向广义RCSFig.2 Backscattering generalized RCSof metal slab with co-horizontal polarization
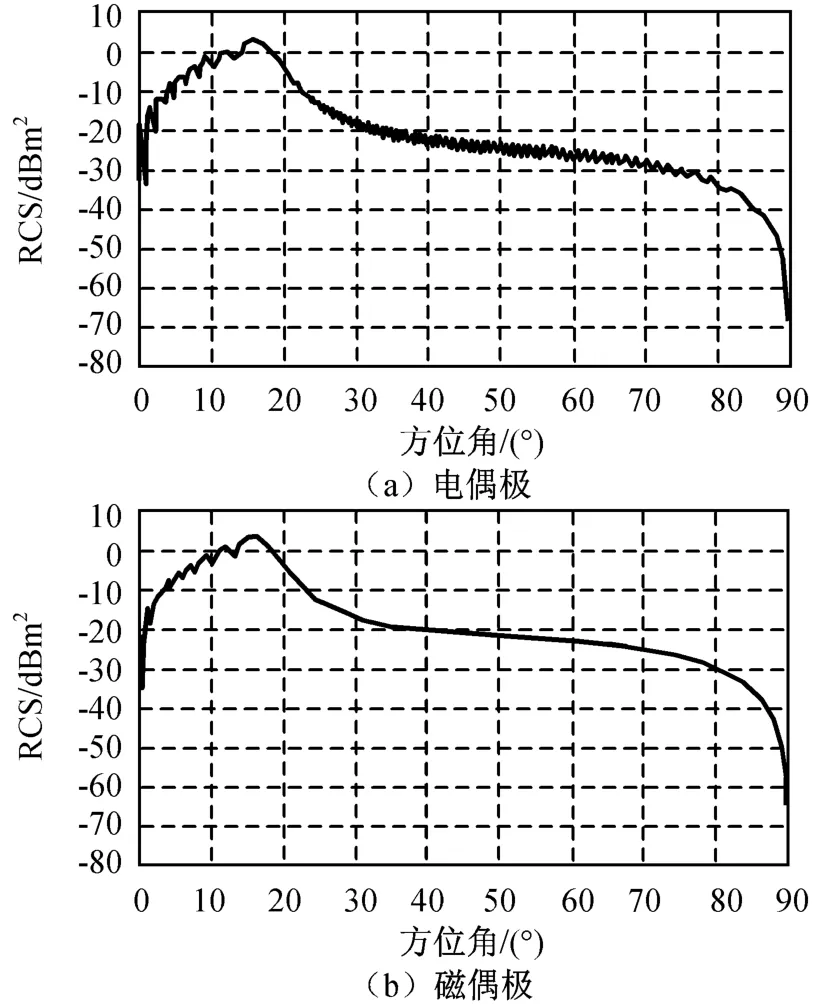
图3 金属平板目标对称交叉极化的后向广义RCSFig.3 Backscattering generalized RCSof metal slab with symmetric-horizontal polarization
由图1~4可知:金属平板目标的与对称极化相关的后向广义RCS明显异于垂直、水平同极化RCS,但不同类型偶极子(电或磁)的极化RCS值相差较小。
在相同计算参数条件下,不同观测距离的与电偶极子对称极化相关的金属平板目标RCS结果分别如图5、6所示。
由图5、6可知:当R较大时,R2σeeSH,R4σeeSS与观测距离无关。
2 广义RCS在近场散射建模中应用
2.1 场分解合成的近场散射建模方法
近场电磁散射的建模计算中,发射及接收天线常采用天线方向图结合球面波等效近似[8、9、11~13]。当天线方向图变化较剧烈时,该近似将引入天线方向图的角度离散误差,而且当天线尺度相对观测距离较大时,以一维天线阵为例,天线各阵元相对目标观测方向与方向图等效观测方向间存在较大偏角,也将引入较大误差,如图7所示。其中,仅当被观测目标在上述偏角范围内的单双站RCS不变时,近场散射计算的天线方向图等效近似才完全成立,若目标电磁散射特性随观测角剧烈变化,该误差可大于10 dB。

图4 金属平板目标对称同极化的后向广义RCSFig.4 Backscattering generalized RCSof metal slab with co-symmetric polarization
根据前文定义的广义RCS,在近场散射计算中进行照射场分解和散射场接收合成,可修正天线方向图等效近似引起的误差,具体建模方法如下。
a)将给定照射及接收天线分解为不同位置偶极子的组合,设强度为Ai(x,y,z),i=1,…,N;
b)用式(2)、(3)分别计算不同偶极子位置处的近场目标散射复函数li;
c)分解偶极子的强度,加权求和步骤b)计算的散射复函数即可获得给定观测天线下近场目标的合成散射复函数为
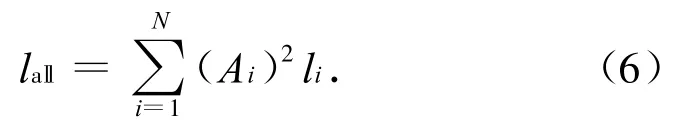
对应地,可用式(1)计算近场散射的合成RCS。
由于振子天线的辐射场随其长度减少与偶极子天线辐射场趋于一致,对实际天线,上述分解中偶极子天线可近似用较小尺寸的振子天线替代,该尺寸大小可根据建模精度的要求选择,通常可取不大于λ/8,此时两者辐射电场的相对偏差小于2.5%。
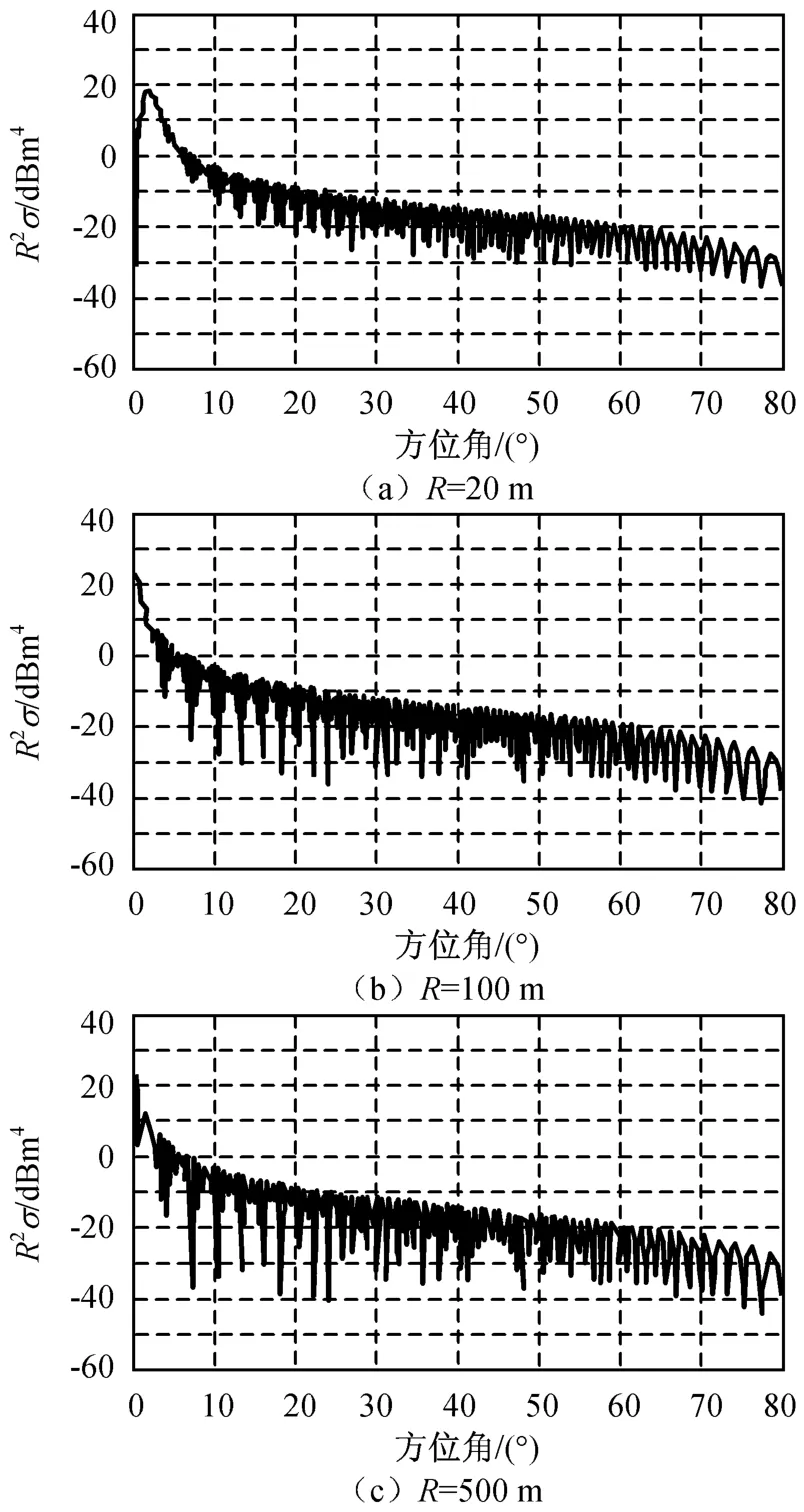
图5 金属平板目标不同观测距离的对称水平交叉极化后向广义RCSFig.5 Backscattering generalized RCS of metal slab with symmetric-horizontal polarization for different observed distance
2.2 仿真结果
假定观测天线由2个相距0.4 m的理想电偶极子天线组成,组合天线中心定为两电偶极子连线的中心;被观测目标为正方形金属平板,边长0.2 m,其中心与两电偶极子间距离相等,λ=16 GHz。用近场电磁散射计算的场分解合成方法和天线方向图等效近似方法,分别计算观测距离为15,10,5,3 m时金属平板目标的合成RCS,不同目标转角(90°时观测方向垂直于金属平板)的两种方法计算的合成RCS分别如图8~11所示。

图6 金属平板目标不同观测距离的对称同极化后向广义RCSFig.6 Backscattering generalized RCS of metal slab with co-symmetric polarization for dif ferent observed distance
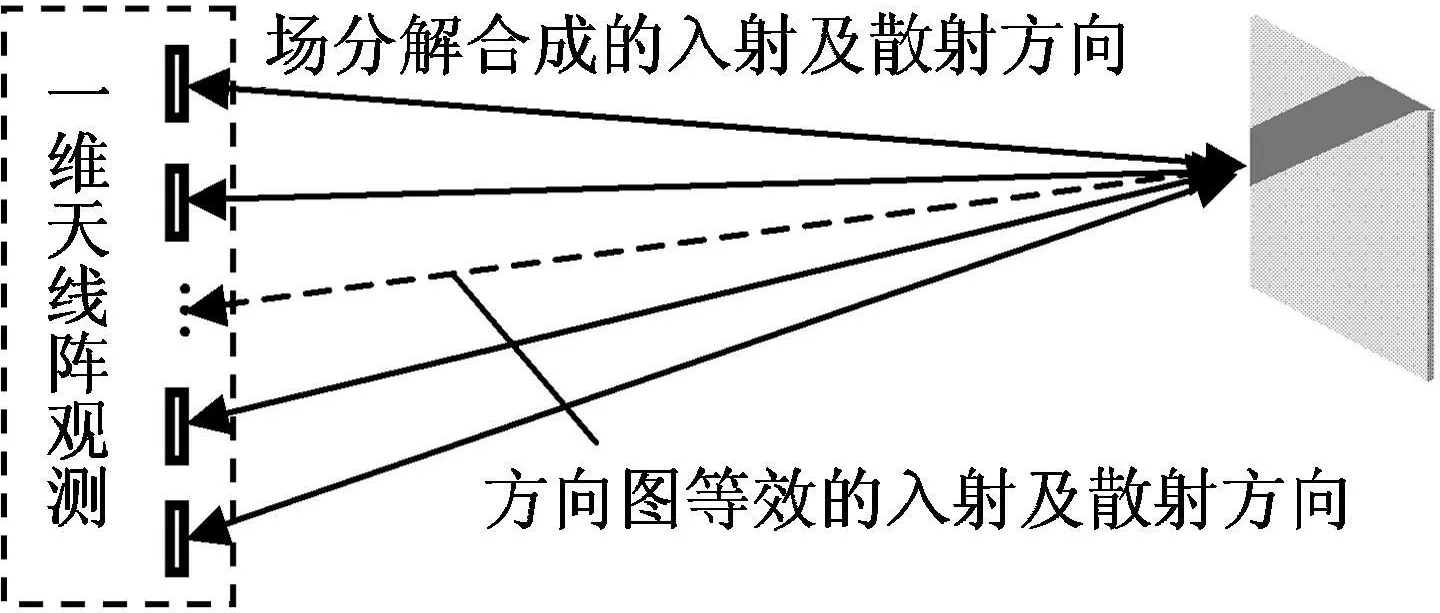
图7 近场散射示意Fig.7 Near-field scattering
由图8~11可知:用天线方向图等效方法计算的最大误差分别为约0.7,2.0,15.0,20.0 dB,用天线方向图等效近似计算的合成RCS误差随观测距离的减少而增大。这主要因为等效近似时天线相对目标的观测角存在较大偏差,如R=5 m时该偏差角为约2.3°,且仿真计算中金属平板目标基元(尺寸约为λ)的后向RCS在目标转角60°附近出现极小值,且变化剧烈,使图8~11中天线方向图等效近似法计算结果在相应角度处出现较大误差。
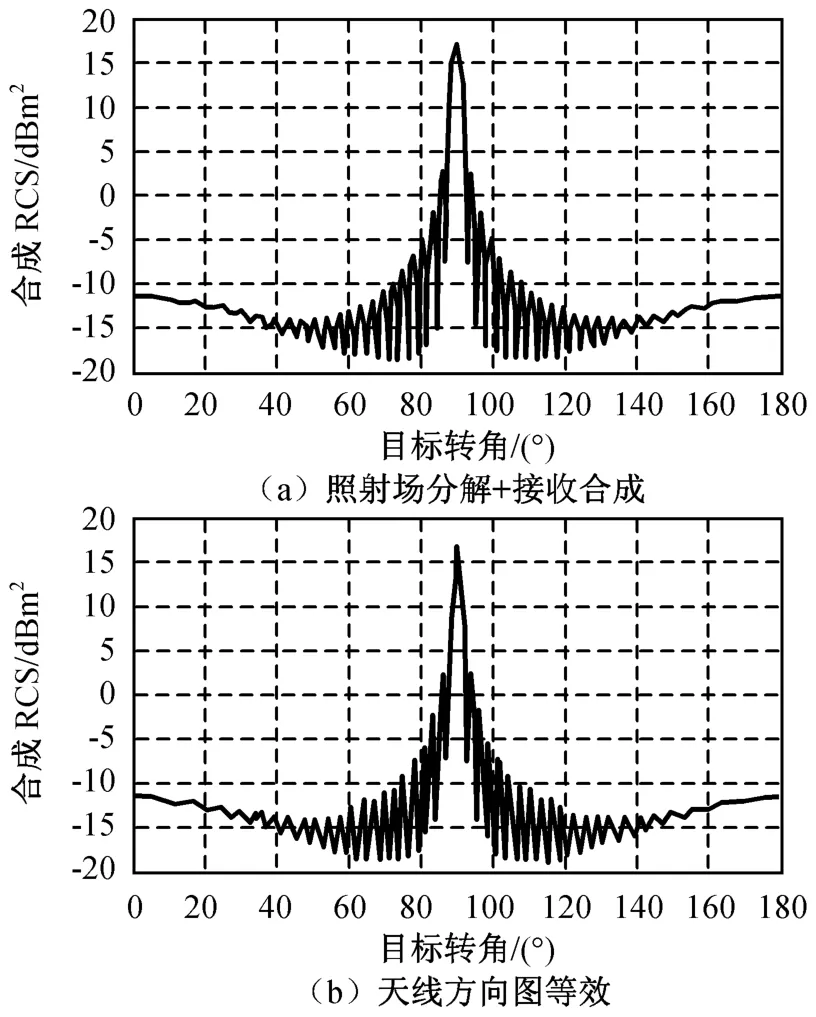
图8 观测距离15 m时金属平板合成RCSFig.8 RCSof metal slab with observed distance15 m
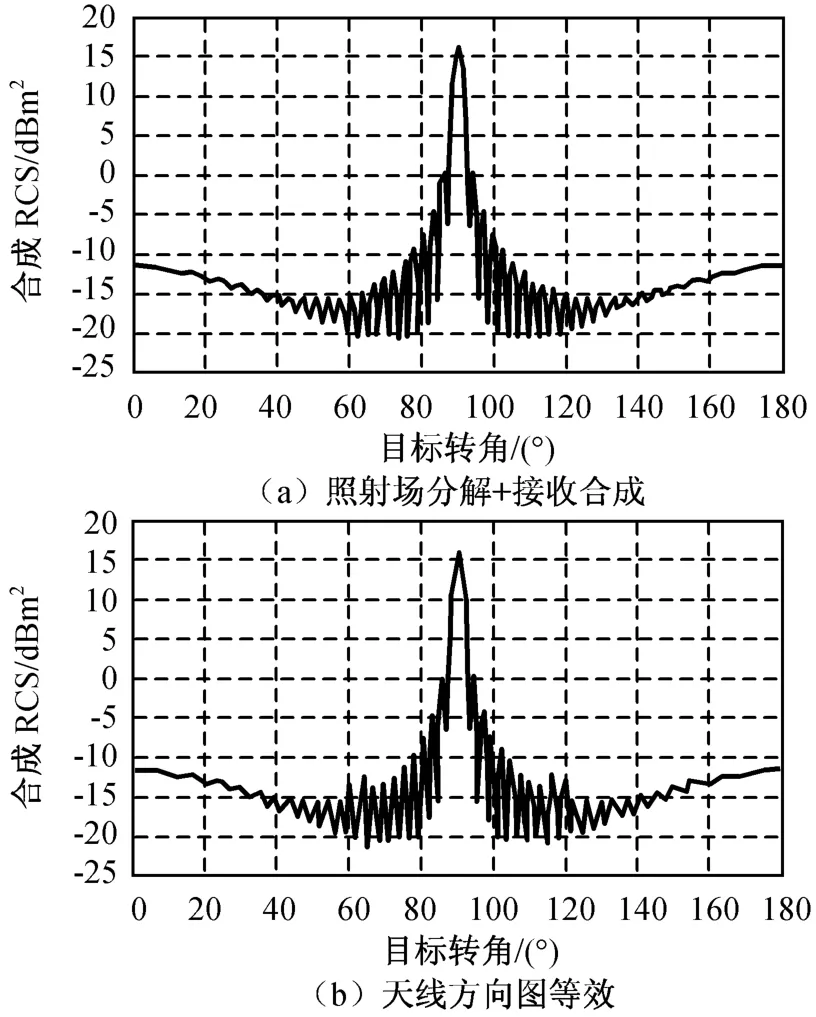
图9 观测距离10 m时金属平板合成RCSFig.9 RCSof metal slab with observed distance10 m
由此可见,天线方向图等效近似方法的计算误差与观测距离、目标RCS起伏特性等相关,在近场局部照射时照射场分解及接收合成方法可有效修正该误差。

图10 观测距离5 m时金属平板合成RCSFig.10 RCSof metal slab with observed distance5 m
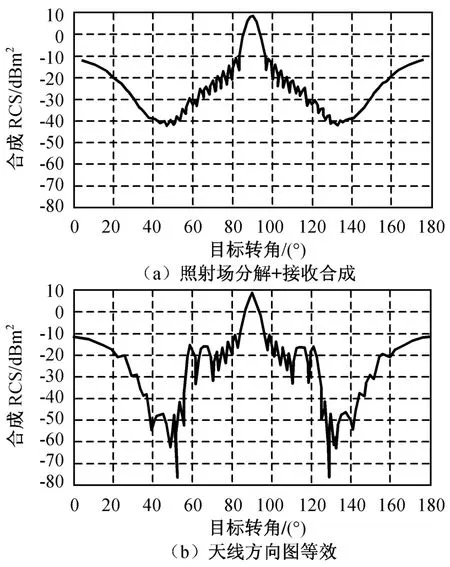
图11 观测距离3 m时金属平板合成RCSFig.11 RCSof metal slab with observed distance3 m
3 结束语
根据电磁场叠加原理,给出了一种与观测天线无关的广义RCS定义,引入了对称极化等36种极化散射特征量,并计算给出了近距离时某金属平板目标极化RCS的变化曲线,表明对称极化RCS是一种较大的近场目标散射特征量;根据广义RCS定义,在近场电磁散射计算过程中进行照射场分解及接收合成,提出了一种有效的近场电磁散射建模方法,并与方向图等效近似方法的计算结果进行了比较,表明近场局部照射时采用场分解合成建模方法的必要性。
[1]阮颖铮.雷达截面与隐身技术[M].北京:国防工业出版社,1998.
[2]MERRILL I S.雷达手册[M].王 军,等(译).北京:电子工业出版社,2003.
[3]黄培康,殷红成,徐小剑.雷达目标特性[M].北京:电子工业出版社,2005.
[4]陈金浩.目标与导弹近区RCS技术[J].制导与引信,1990,11(3):1-11.
[5]李 铁,马岸英.近场RCS标定问题[J].制导与引信,1996,17(4):65-69.
[6]TAYLOR J M.On the concept of near field radar cross section:IEEE Antennas and Propagation Society International Symposium[C].IEEE,1997,2:1172-1175.
[7]金灿民,许家栋,韦 高.复杂目标近场电磁散射的可视化计算方法[J].电波科学学报,1998,13(3):241-244.
[8]陶建锋,盛孝鹏,孙 青.复杂目标的近场散射特性分析[J].现代雷达,2006,28(10):75-78.
[9]张京国,梁晓庚.基于物理光学法和面元法的目标近场RCS计算[J].探测与控制学报,2008,30(6):42-45.
[10]何国瑜,陈海波,苗俊刚,等.近场散射与远场RCS的链条关系式[J].微波学报,2006,22(4):1-4.
[11]陈立平,吴嗣亮.引信目标模拟器中回波的建模与仿真[J].北京理工大学学报,2005,25(12):1099-1102.
[12]何 凡,李少洪,陈 炜.HPRF-PD体制引信的回波仿真与多普勒频率提取[J].遥测遥控,2005,26(3):55-58.
[13]潘 曦,崔占忠.无线电引信近场目标特性研究[J].兵工学报,2008,29(3):277-281.
