一类反对称特征值问题的向后误差

庞澄澄,王卫国

(中国海洋大学数学科学学院,山东青岛266100)

一类反对称特征值问题的向后误差

庞澄澄,王卫国

(中国海洋大学数学科学学院,山东青岛266100)

本文研究一类反对称特征值问题在实扰动情形下的向后误差。该问题的系数矩阵同时具有反对称性和零块结构。本文将给出范数型双结构向后误差的表达式,并将所得结果与一般的反对称结构向后误差进行比较。数值实验结果表明,双结构向后误差和反对称结构向后误差的比值有时会非常大。

结构特征值问题;双结构;向后误差

0 引言

考虑特征值问题

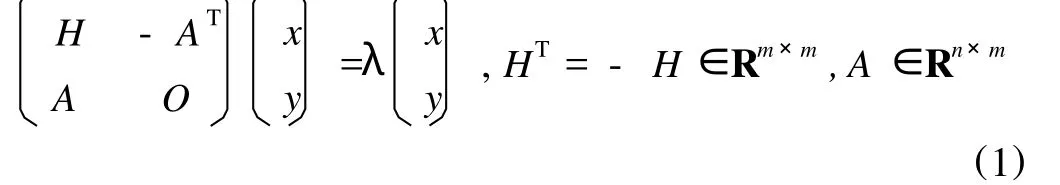
在研究Stiefel流形上的测地线计算[1]时,导出上述问题。

Higham和Higham[2]指出,向后误差及条件数在现代数值代数中是2个重要的概念。前者反映数值方法的向后稳定性;后者揭示问题的解关于数据扰动的敏感性。在一阶近似下,二者结合可给出计算解的误差估计:

计算解误差≾向后误差×条件数。

对于问题(1),系数矩阵具有反对称性及零块结构。如文献[2]所指出的,对于结构问题,应该考虑结构向后误差与结构条件数,一阶近似下,计算解的误差估计为:

计算解误差≾结构向后误差×结构条件数。

关于结构向后误差分析,已有很多研究。Sun研究了KKT方程组的结构向后误差[3]。Tissuer归纳了包括反对称结构在内的约90种结构特征值问题的向后误差分析的结果,其中一部分是作为待解决问题提出的[4]。对于系数矩阵为Hermite阵的特征值问题的结构向后误差,Higham对广义特征值问题进行了相关研究[2],Tisseur考虑了多项式特征值问题[5], Hachstenbach和Plestenjak研究了多参数特征值问题[6]。刘新国等在近些年研究了多种特征值问题的向后误差,其中包括Hermite阵,酉阵,一类周期辛矩阵等[7-10]。有关特征值问题(1)的向后误差还未见到研究。

本文主要研究该特征值问题的结构向后误差。对于实矩阵,求解相应特征值问题的时候一般尽量规避复运算(比如双位移QR方法),因此,本文主要研究实扰动情形。

1 预备

1.1 一般反对称结构向后误差

问题(1)可简写为

1.2 四个引理

在本文以下推导过程中,将用到以下引理。

此结果给出了矩阵方程XB=C的解X的明显表达式。

引理1[11]设B∈Rn×p,C∈Rm×p已给定。定义集合

这里Z∈Rm×n,B+表示B的广义逆。

下述结果给出了方程HB=C的反对称解H的明显表达式。

引理2[4]设B,C∈Rn×l已给定。定义集合

即,实部x(1)和虚部x(2)正交,并且等长。

2 双结构向后误差

这里

3 数值实验

所有数值实验的计算都是使用Matlab7.0运行的,相对机器精度约为2.2202×10-16。将(2)定义的一般反对称结构向后误差η()简记为η,将(4)定义的双结构向后误差η)简记为ηD。

取m=3,n=4,随机生成H和A,要求HT=-H∈R3×3,A∈R4×3。使用order[V,D]=eig()得到近似特征值和特征向量。选择第一个特征值λ,以及相应的特征向量z ,来计算ηD/η的值。

将100次实验得到的结果用图1表示。可以看出,大部分ηD/η的值比较小,在[1.4,10]之间扰动,只有很少几个ηD/η的值相差很大。例如,取

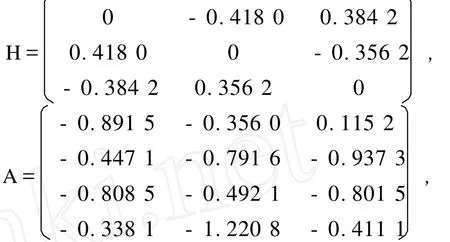
可得到ηD/η=239.983 3。

图1 计算100次的结果Fig.1 The results of computing one hundred times

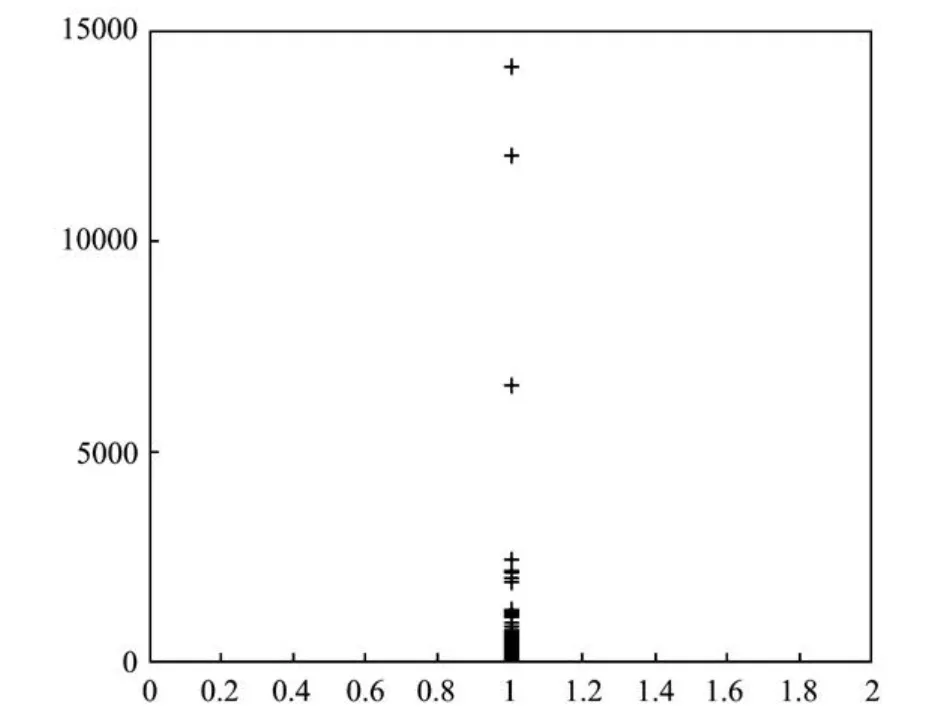
图2 计算10 000次的结果Fig.2 The results of computing ten thousand times

将10 000次实验得到的结果用图2表示。可以看出,大部分ηD/η的值在[1.4,300]之间,只有几个ηD/η的值会相差比较大。例如,取

可得到ηD/η=3.325 7×103。但这些少量的ηD/η的值表明,双结构向后误差在某些情形比单结构向后误差可以大很多。

[1] Edelman A,Arias T A,Smith S T.The geometry of algorithms with orthogonally constraints[J].SIAM J Matrix anal Appl, 1999,20(2):303-353.

[2] Higham D J,Higham N J.Structured backward error and condition of generalized eigenvalue problems[J].SIAM J Matrix Anal Appl,1998,20(2):493-512.

[3] Sun J G.Structured backward errors for KKT systems[J].Linear Alg Appl,1999,288:75-88.

[4] Tisseur F.A chart of backward errors for singly and doubly structured eigenvalue problems[J].SIAM J Matrix Anal Appl,2003, 24(3):877-897.

[5] Tisseur F.Backward error and condition of polynomial eigenvalue problems[J].Linear Alg Appl,2000,309(1-3):339-361.

[6] Hochstenback M E,Plestenjak B.Backward error,condition numbers,and pseudospectra for the multiparameter eigenvalue problem [J].Linear Alg Appl,2003,375:63-81.

[7] Xin-Guo Liu,Ze-Xi Wang.A note on the backward errors for Hermite eigenvalue problems[J].Appl Math Comput,2005,165 (2):405-417.

[8] 刘新国,栾世宝.一类周期辛矩阵对特征值问题的向后误差分析[J].山东大学学报:工学版,2007,37(1):94-98.

[9] 司玉琨.结构酉阵特征值问题向后扰动分析[D].青岛:中国海洋大学,2005.

[10] 王泽玺.两类系统的向后误差及条件数[D].青岛:中国海洋大学,2005.

[11] 孙继广.矩阵扰动分析第二版[M].北京:科学出版社,2001.

Abstract: This paper deals with backward errors for a class of skew-symmetric eigenvalue problems.For the doubly structure,both skew-symmetric structure and zeroth structure are considered.We derive explicit formula for the doubly structured normwise backward error,and compare the results with the single structured case.Numerical results demonstrate that the ratio of doubly structured backward error and the single structured one can be large.

Key words: structured eigenvalue problem;doubly structure;backward error

AMS Subject Classification: 15A18

责任编辑 朱宝象

Backward Errors for a Class of Skew-Symmetric Eigenvalue Problems

PANG Cheng-Cheng,WANG Wei-Guo
(School of Mathematics Science,Ocean University of China,Qingdao 266100,China)

O241.1

A

1672-5174(2011)06-130-05

国家自然科学基金资助项目(10971204);山东省自然科学基金资助项目(Y2008A07);中央高校基本科研业务费专项(201013048)资助

2010-11-20;

2011-03-24

庞澄澄(1985-),女,硕士生。E-mail:pcc192295@163.com