(Ga)12N，(Ga)12B荷电团簇的电子结构与磁性

李顺江，代武春

(重庆文理学院物理系，重庆 永川 402160)

镓是蓝白色金属，镓的化合物半导体广泛用于电子与微电子工业，可作红外光学与红外探测器件、微波通讯与微波集成、集成电路，也可作红、黄、蓝、绿与白色的发光二极管，GaAs太阳能电池是迄今转换率最高的.镓具有很复杂的晶体结构，龚新高［1］采用第一性原理分子动力学方法，在让原子得到充分弛豫后，计算了固体镓的电子结构.通过计算总能随体积的变化，讨论了零温度下镓的相对稳定性，结果表明在α-Ga中，最近邻原子之间存在共价性从而导致电阻各向异性，而镓的其它相均为良好金属.团簇是由几个乃至上千个原子、分子或离子通过物理或化学结合力组成的相对稳定的微观或亚微观聚集体，它可以作为物质由原子、分子向块体物质转变过程中的特殊物相，因此，人们对镓团簇展开了广泛的研究.Song［2］等人利用FP-LMTO方法计算了Ga5N5团簇的结构，得到了一种平面稳定结构，郝静安［3］等人在密度泛函理论的基础上，对Ga6N6团簇进行了第一性原理、全电子从头计算，得到了10种可能的3维空间结构及其电子结构.马文瑾［4］等用密度泛函理论的B3LYP方法，在6-31G*水平上对 GamN(m=1～9)团簇的几何构形、电子结构、振动频率等性质进行了理论研究，得出N原子在Gam团簇内结合形成的结构较稳定，即N原子位于线状结构的集合中心以笼状结构的内部时，结构的稳定性增大.李恩铃［5-6］等用 B3LYP-DFT方法对 GanN(n=1～7)和GanN(n=2～8)团簇的结构与稳定性进行了研究，在6-31G*水平上进行了结构优化和频率分析，得到了GanN2(n=1～7)和GanN(n=2～8)团簇的基态结构.李恩铃［7］等用密度泛函理论的B3LYP-DFT方法在6-31G*水平上对GanN+(n=2～8)和 GanN2+(n=1～7)阳离子团簇的几何结构、稳定性和振动频率等进行研究，得到GanN+(n=2～8)和 GanN2+(n=1～7)阳离子团簇的基态结构.由于镓的掺杂团簇是一种宽带半导体材料，在微电子和光电领域均显示出其广阔的应用前景.本文拟对Ga13掺杂B，N的荷电团簇的电子结构与磁性进行研究.

1 计算方法

通过自洽迭代方法求解上述方程可得团簇的总能量，进而可得束缚能、HOMO与LUMO间的能隙、局域电荷等性质，全部构型优化和电子结构计算均采用DMOL软件包.在广义梯度近似(GGA)中，选择 Becke［8］的交换梯度修正和 Perdew［9］的关联梯度修正，采用带极化的双数值原子基组(DNP)完成全电子自旋无限制的计算.几何优化的收敛标准设置为能量梯度10-4eV·Å-1和原子位移5×10-4Å，电荷密度收敛于10-8，总能量收敛为10-6eV.在团簇几何优化和能量计算中，我们在缺省轨道占据Smearing参数下计算能量、轨道和布居数.

团簇的束缚能定义为BE=Et-Ea，其中Et为团簇的总能量，Ea为各原子的能量之和.按此定义，团簇的束缚能为负.

分布态密度(PDOS)的计算根据洛仑兹表达式:

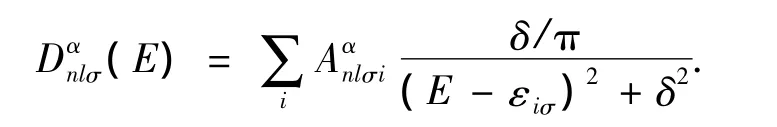
将每个分离的能级展宽，即可得到电子自旋σ的分布态密度(PDOS).总的态密度(TDOS)由下列表达式定义:

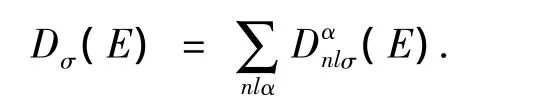
计算过程是:1)荷电团簇的掺杂.采用B，N分别代替Ga13团簇的中心原子或表面原子，计算团簇的束缚能、键长和电子结构.2)电子态密度计算.将(Ga)12N，(Ga)12N团簇置于晶格常数为15Å的立方元胞中计算其电子总态密度(TDOS)和分布态密度(PDOS).

2 结果与讨论

2.1 电子结构

采用密度泛函理论和以密度泛函理论为基础的DMOL软件包分别对(Ga)12B，(Ga)12N的几何结构进行优化，优化结果如图1所示.图1(a)是Ga13团簇的结构，图1(b)表示具荷电团簇，图1(c)表示掺杂中心的荷电团簇.

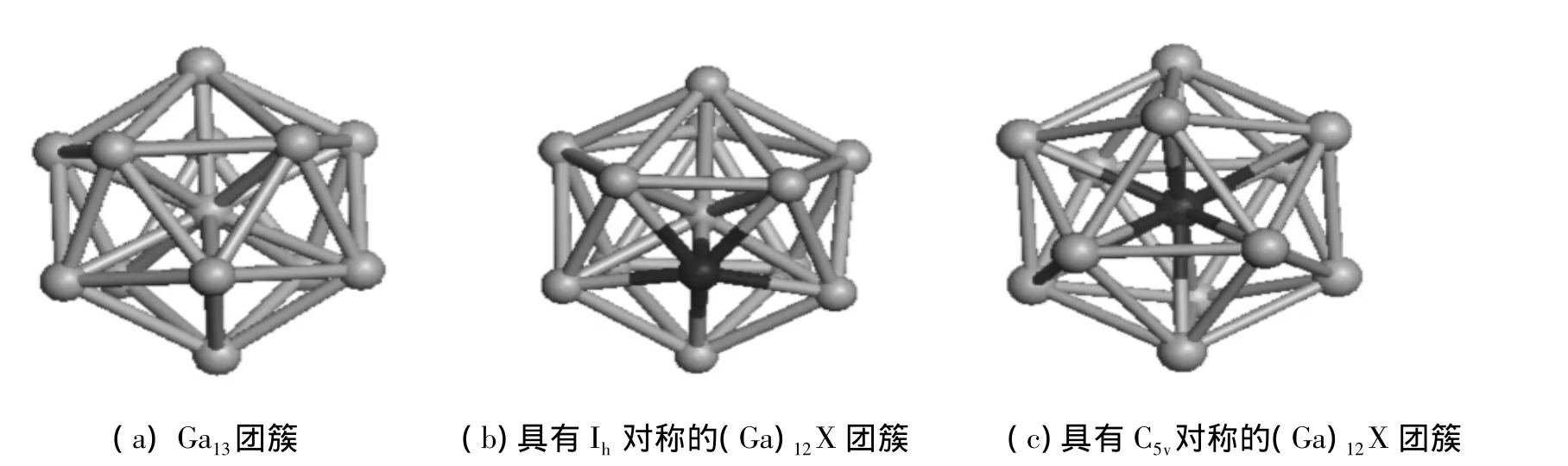
图1 Ga13团簇及(Ga)12X团簇的几何构形

表1 具有C5v对称的二十面体(Ga)12X荷电团簇的束缚能BE，中心原子到表面原子的距离r，HOMO与LUMO能隙ΔE，总磁矩S和原子电荷Q

表2 具有Ih对称的二十面体(Ga)12X荷电的束缚能BE，中心原子到表面原子的距离r，HOMO与LUMO能隙ΔE，总磁矩S和原子电荷Q

由表1可知:与Ga13团簇相比，C5v对称性结构的(Ga)12X(X=B，N)带1个正电荷时，团簇的束缚能增大，HOMO与LUMO能隙△E减小，带1个负电荷时，团簇的束缚能降低，HOMO与LUMO能隙△E减小.当掺入杂质离子X±后，中心原子到表面原子的距离减小(Ga12B1+除外)，总磁矩未发生变化仍为零，表现出非磁性，掺杂团簇(Ga)12B1-的束缚能最低为-32.38eV，是C5v对称性结构中最稳定的结构.

由表2可知:与Ga13团簇相比，Ih对称性的(Ga)12X(X=B，N)带1个正电荷时，团簇的束缚能增大，HOMO与LUMO能隙△E增大，带1个负电荷时，团簇的束缚能降低，HOMO与LUMO能隙△E减小，总磁矩都为零(除Ga12B1+外).当掺入杂质X±后，中心原子到表面原子的距离降低，除(Ga)12B1+外的磁矩发生变化外，呈现出磁性，其余均未发生变化，掺杂团簇(Ga)12B1-的束缚能最低为-33.77eV，是Ih对称性结构中最稳定的结构.

比较表1和表2可以看出:1)当掺入杂质X及所带电荷一定时，(Ga)12X荷电团簇的C5v对称性结构比Ih对称性结构的束缚能高，HOMO与LUMO能隙△E更窄.2)具有C5v和Ih对称性结构的除Ih对称性结构的(Ga12B1+)有磁矩外，其他的均无磁矩.3)用X±代替Ga13团簇的中心或表面原子，能提高Ga13团簇的稳定性(带正电的除外).4)具有C5v和Ih对称结构的(Ga)12X荷电团簇的HOMO都形成闭壳层(Ga12B1+除外).

由于掺杂原子N和B的原子量比Ga小很多，由表1和表2可以看出:(Ga)12B和(Ga)12N荷电团簇的束缚能在具有Ih对称性结构时更低，与在金属 Al13团簇中掺杂原子 C，Si，Ge，Sn，Pb形成的团簇Al12X的束缚能随原子量的变化关系类似［10］，从理论上可以得出，当掺杂原子比团簇主体原子的原子量小很多时，具有Ih对称的团簇更稳定.

2.2 态密度分析

从以上分析可以得出，掺杂的荷电团簇具有Ih对称性结构的荷电团簇更稳定，为了进一步证明这个观点，下面我们用态密度对其进行分析.

图2至图5给出了具有Ih对称和C5v对称的(Ga)12B1-和(Ga)12N1+电子总态密度和分布态密度随能量的变化.由图2可以看出，在具有Ih对称的Ga12B1-团簇中，电子总态密度在远离费米面处的峰值是中心B原子的s，p轨道和表面Ga原子的d轨道杂化引起的.由图3可以看出，在具有C5v对称的(Ga)12B1-团簇中，电子总态密度在远离费米面处的峰值是由中心Ga原子的s，d轨道在远离费米面处的峰值决定的，原子间并未发生杂化.由此可以看出，具有Ih对称性的(Ga)12B1-团簇比C5v对称性的(Ga)12B1-团簇更稳定，因为前者在远离费米面的峰值是原子间的轨道杂化引起的，而后者在远离费米面的峰值是远离费米面的中心Ga原子的d轨道在远离费米面的峰值引起的.

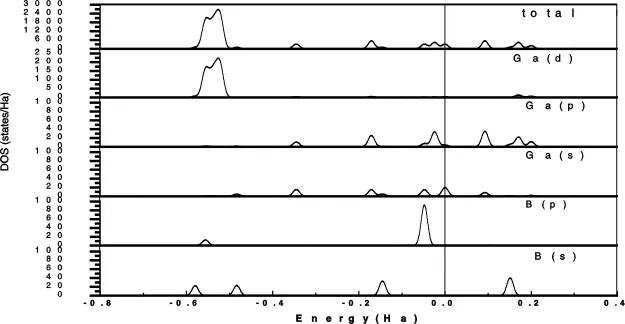
图2 Ih对称性结构(Ga)12B1-荷电团簇的电子总态密度和分布态密度

图3 C5v对称性结构(Ga)12B1-荷电团簇的电子总态密度和分布态密度

图4 Ih对称性结构(Ga)12N1+-荷电团簇的电子总态密度和分布态密度

图5 C5v对称性结构Ga12N+1荷电团簇的电子总态密度和分布态密度

同理，我们也可以从图4看出，在具有Ih对称性的(Ga)12N1+荷电团簇中，电子总态密度在远离费米面处的是中心原子N原子的s，p轨道和表面Ga原子的d轨道杂化引起的.由图5可以看出，在具有C5v对称的(Ga)12N-团簇中，电子总态密度在远离费米面处的峰值是由中心Ga原子的d轨道和N原子的s轨道杂化引起的.由此可以看出，具有Ih对称性的(Ga)12N-团簇比C5v对称性的(Ga)12N-团簇更稳定.上述研究表明，具有Ih对称性的荷电团簇比C5v对称性的荷电团簇更稳定.

2.3 磁性的研究

团簇的磁性主要受以下几大因素影响:1)维度.由于团簇低维度的特点，团簇中电子占据d轨道的宽度比块体中电子占据d轨道的宽度更小，使其产生的磁矩更大.2)对称性.对称性越高，简并度越大;电子占据的态密度越窄磁矩越大，态密度越宽磁矩越小.3)交换劈裂.交换劈裂可以引起上自旋往下移动，下自旋往上移动，这种移动将会导致自旋向上与自旋向下之间的电子数目发生变化，而这种变化的差距可以决定团簇磁矩的大小.交换劈裂的值越大，磁矩越大;交换劈裂的值越小，磁矩越小.4)掺杂原子对主体原子的影响.主体原子d轨道电子数目变化很小，而磁矩变化很大，这很难说明磁矩来自于掺杂原子与主体原子间电荷的转移.

对于1)、2)两个影响团簇磁性的因素在此不作讨论.对于交换劈裂对团簇磁性的影响，由图6可知，在Ih对称性结构(Ga)12B1+荷电团簇中，杂质原子B的电子态密度交换劈裂的值较大，导致其磁性明显，对团簇的磁性产生了较大影响.由表2可以看出，(Ga)12X荷电团簇表面原子向中心原子转移的电荷小于Ga13团簇的电荷转移，因此掺杂荷电团簇中的电荷转移情况对团簇磁性有重要影响.

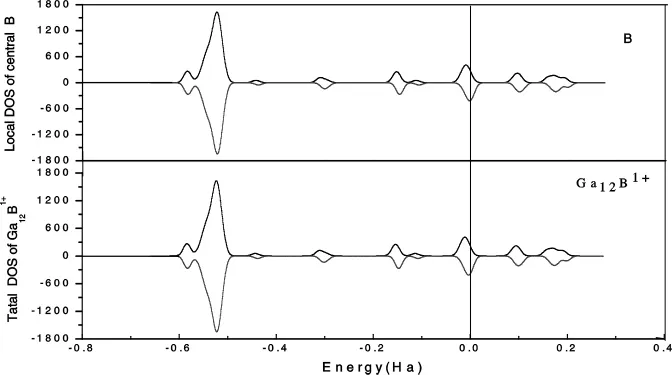
图6 Ih对称性结构(Ga)12B1+荷电团簇的电子分布态密度和B原子的电子分布态密度

表3 Ga12X荷电团簇的局域磁矩和电荷

表3分别列出了Ga13和荷电团簇的局域磁矩和电荷.由表3可以看出:1)荷电团簇的局域磁矩都为零，没显出磁性(Ih对称性结构(Ga)12B1+除外).2)Ih对称性结构(Ga)12B1+荷电团簇的主体原子与掺杂原子的自旋方向相反，则表明这个团簇的主体原子或掺杂原子呈现出抗磁性.

从图7可以看出，只有 Ih对称性结构(Ga)12B1+荷电团簇形成交换劈裂，其它的都没有，所以Ih对称性结构(Ga)12B1+荷电团簇有磁性，其它的均显出非磁性.

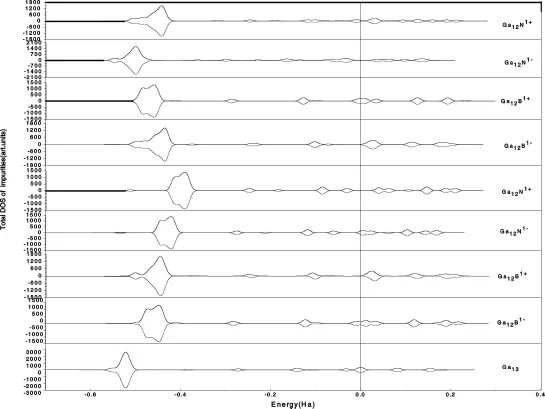
图7 Ga13荷电团簇和(Ga)12X荷电团簇的电子分布态密度

3 结论

1)当掺入杂质 X及所带电荷一定时，(Ga)12X荷电团簇的C5v对称性结构比Ih对称性结构的束缚能高(除Ga12B1+外)，HOMO与LUMO能隙△E更窄.

2)用X±代替Ga13团簇的中心或表面原子，能提高 Ga13荷电团簇的稳定性(除带正电的外);具有C5v和Ih对称性结构的(Ga)12X荷电团簇的HOMO都形成闭壳层(Ga12B1+除外).当掺杂原子比主体原子的原子量小很多时，具有Ih对称性结构的荷电团簇更稳定，且为(Ga)12B1-团簇最稳定.

3)Ih对称性结构(Ga)12B1+荷电团簇有磁矩产生且在态密度分析中形成交换劈裂，显出磁性;其它团簇均无磁矩产生并显出非磁性.

［1］龚新高.固态镓的电子结构［J］.物理学报，1993，42(4):1025-1037.

［2］Song B，Cao P L.Theoretical study of structures of Ga3N3cluster［J］.Phys.Lett.A，2002，300:485-490.

［3］郝静安，郑浩平.Ga6N6团簇结构性质的理论计算研究［J］.物理学报，2004，53(4):1044-1019.

［4］马文瑾，张静，王艳宾，等.GamN(m=1～9)团簇结构与稳定性的量子化研究［J］.化学学报，2007，65(12):1110-1116.

［5］李恩玲，陈贵灿，王雪文，等.从头计算对GanNm团簇的结构与稳定性的研究［J］.原子与分子物理学报，2007，24(3):447-459.

［6］李恩玲，马红，陈贵灿，等.GanNm+(n=1～8，m=1～2)团簇的结构及稳定性的DFT研究［J］.计算物理，2007，24(4):480-486.

［7］李恩玲，王雪雯.GanNm-阴离子团簇的结构及稳定性的研究［J］.物理学报，2006，55(5):2249-2256.

［8］Becke A D.Correlation energy of an inhomogeneous electron gas:a coordinate space model［J］.J.Chem.Phys.，1988，88:1053.

［9］Perdew JP，Wang Y.Accurate and simple analytic rep resentation of the electron gas correlation energy［J］.Phys.Rev.B，1992，45:13244.

［10］Li SF，Gong X G.Neutral and negatively charged Al12X(X=Si，Ge，Sn，Pb)clusters studied from first principles［J］.Phys.Rev.B，2006，74:45432.