基于分子动力学对超晶格结构界面热阻的模拟研究
2011-09-12张兴丽孙兆伟
张兴丽, 孙兆伟
(哈尔滨工业大学卫星技术工程研究所,哈尔滨 150001)
超晶格结构材料是两种或两种以上材料按照周期性结构排列而形成的复合材料,具有良好的热电性质,能显著提高热电转换设备效率,在计算机芯片、MEMS器件、航空航天等领域有广泛应用。对超晶格材料进行传热分析是当今的热点问题,因为超晶格材料的尺寸达到了微/纳米量级,经典热传导理论已经不能正确解析体系内非常规传热特性[1]。传热学及传热分析方法正面临着从宏观向微观理论和方法过渡,许多理论及研究方法急需从更高层次和深度来观察与解决。分子动力学模拟方法就是探求微/纳尺度条件下的热现象的规律和内在机制的有效方法,它可以从微观细节着手,研究热载流子(如声子和电子)的行为,并依据统计力学原理得到系统的宏观性质。从统计物理的角度可以将分子动力学分为平衡分子动力学模拟(EMD)和非平衡分子动力学模拟(NEMD)两种模拟方法。前者是计算平衡系统的热流与时间的相关函数,然后通过Green-Kubo关系式得到热导率;后者需要对系统施加能量产生热流,得到系统的温度梯度,根据Fourier定律计算热导率[2~4]。
界面热阻是热载流子在两接触固体界面层相互作用的结果。在微观传热领域内,不同材料间界面热阻的计算是当前研究的热点问题,因为界面热阻直接影响到材料的热传导性能,从而对微/纳米器件的设计和热优化产生影响。利用分子动力学方法对界面热阻进行计算机模拟,可以从不同角度对界面热阻的内在机理进行探讨。分子动力学(MD)模拟通过求解牛顿运动方程得到每个粒子空间位置和运动状态随时间的演进状况,在计算界面热阻时,它不需要考虑每个粒子本身的散射特性,而只需根据势能函数确定粒子之间的相互作用规律[5~8]。
本工作以Si/Ge超晶格结构为例,利用非平衡态分子动力学模拟方法从微观机制出发研究超晶格结构界面热阻的一些变化趋势。
1 分子动力学模型
本工作所采用的超晶格结构导热模型如图1所示。模拟对应的硅的晶格常数为0.543nm,锗的晶格常数为0.5657nm。在X方向上布置随机恒温热墙以建立热流方向的温度梯度,高温热墙和低温热墙的材料均与各自临近的超晶格材料相同,并设定其厚度为3UC(UC,晶格长度);在Y,Z方向施加周期性边界条件,由于垂直热流方向的横截面积过小会对热导率的计算结果产生误差[9],因此设定YOZ横截面积为4UC×4UC;模型的最外层设置厚度为2UC的绝热壁,它的作用是减少导热层内的粒子蒸发,防止与外界产生热量交换,并且设定该区域粒子的速率为0。

图1 硅锗超晶格结构非平衡分子动力学模拟模型Fig.1 The NEMD simulation model of Si/Ge superlattice structure
利用非平衡分子动力学方法模拟了平均温度为400K时不同周期长度的硅锗超晶格薄膜热导率。模拟中采用Stillinger-Webber多体势能函数来描述硅、锗分子之间的相互作用[10,11];采用 Verlet推导的Leap-frog算法进行粒子运动方程的数值积分。由于模拟过程中的平衡温度低于Si的Debye温度(645K),因此需对系统的局域稳定进行量子化修正,才能获得超晶格结构界面热阻的真实值。根据经典Boltzmann统计可以获得第j层中局域温度为:

式中,[]...表示在总的模拟时间内的统计平均;kB是Boltzmann常数;Nj为第j层的粒子数。依据经典统计下的能量均分定理,第j层中的能量等式可以表示为:
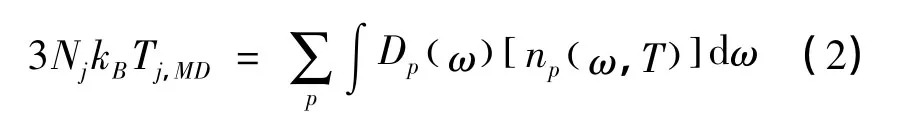
式(2)右边是系统中粒子的总能量,D()ω为声子密度分布函数;ω为声子频率;n为对应于热平衡温度T的声子平均占有数,该占有数满足Planck分布(即Bose-Einstein统计)。
在Debye近似下,能量等式(2)可以转化为:
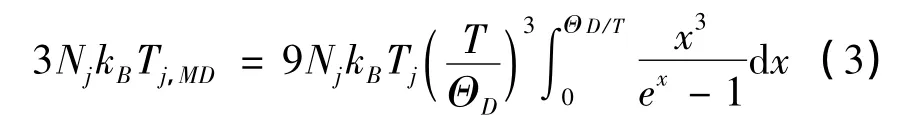
通过数值求解式(3),得到与分子动力学模拟(MD)的局域温度Tj,MD相对应的真实晶格温度Tj。
当高温热墙或低温热墙的粒子与其他粒子作用时,温度会发生改变。为使在导热层区域形成稳定的温度梯度,需要通过改变粒子的速率来增加高温热墙一定数量的动能,同时从低温热墙移出同等数量的动能。高、低温热墙能量的变化量可以表示为:
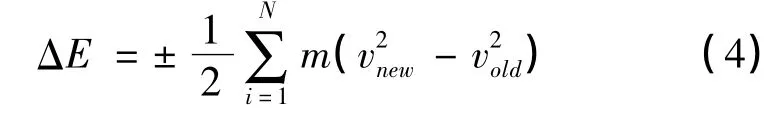
通过温度梯度方向(X方向)的热流计算公式为:
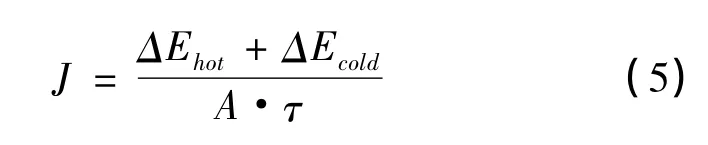
式中A为热流方向的横截面积;τ为模拟的时间步长。
超晶格结构两种材料界面的示意图如图2所示。假设在连接区域的原子散射都是弹性的,这样可忽略连接区域长度的影响,界面热阻近似等于连接区域的热阻[12],界面热阻可定义为:
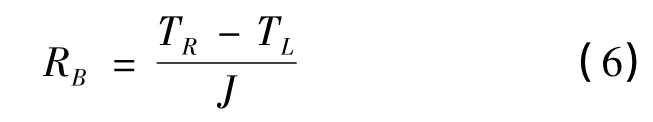
式中TR,TL分别为界面左右两端的温度。
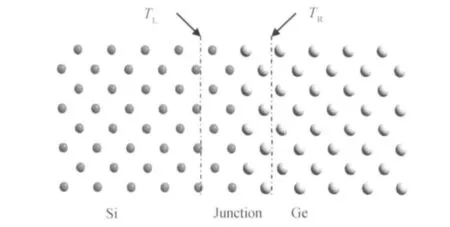
图2 硅锗超晶格结构界面示意图Fig.2 Schematic diagram of the Si/Ge superlattice interface
3 结果和讨论
非平衡分子动力学模拟在微正则(NVE)系统条件下进行,模拟的时间步长为1fs,总的模拟步长数为5×106,其中前2×106步使系统平衡。在不同的模拟温度下,高低温热墙的温度设为Thot=T+20 K及Tcold=T-20 K以形成温度梯度。
图3为周期长度为10UC的硅锗超晶格薄膜在平均温度为500K时从高温热墙到低温热墙导热层温度示意图,从图中可以明显看出受界面热阻的影响在硅锗界面处温度存在明显的跳跃。三个硅锗交界面的温度变化值ΔT分别约为19K,10K,8K,由式(6)可知靠近高温热浴的第一个界面热阻要远远大于其余界面,这个模拟结果与Abramson等[13]的研究成果相一致。他指出界面热阻与界面数之间变化的非线性行为,是由于不同界面间传递热流的声子振动频率不同致使热流穿过每个界面产生的热阻也不同。因此,最靠近高温热浴的界面热阻比其余界面大,这也与传递热流的声子类型不同有关。
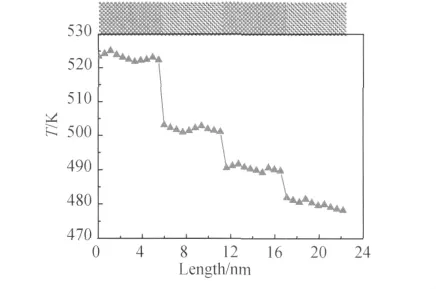
图3 导热层长度方向的温度分布图Fig.3 The temperature profile along the length of simulation cell for Si/Ge superlattice system
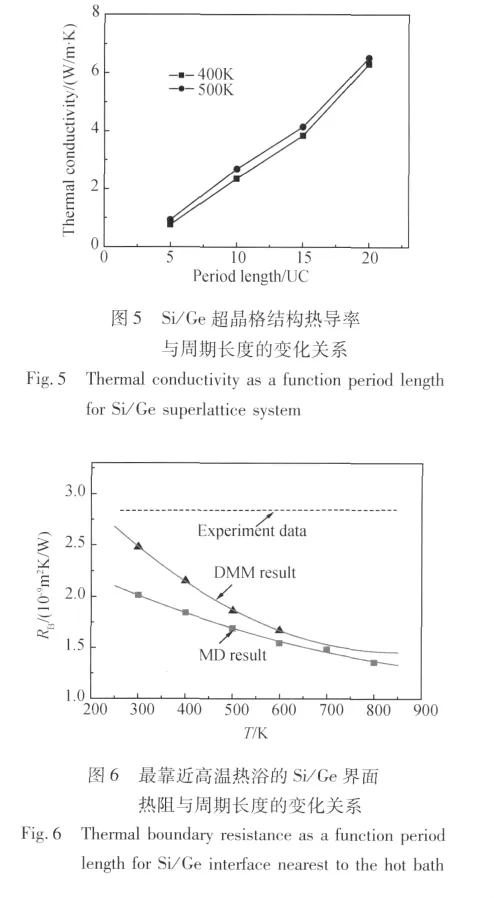
图4是温度为400K和500K时利用分子动力学模拟计算的最靠近高温热浴的Si/Ge界面热阻随周期长度的变化。由图4可知随着周期长度的增大,该界面热阻逐渐减小,因此界面热阻在总热阻中所占的比例逐渐减小,界面效应减弱,Si/Ge超晶格薄膜的热传导性能不断提高(如图5所示)。
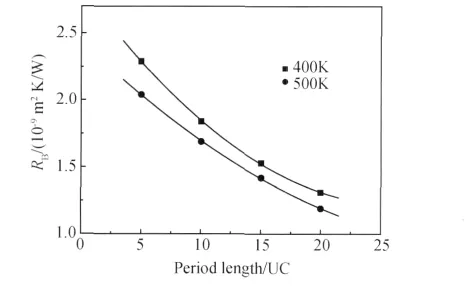
图4 最靠近高温热浴的Si/Ge界面热阻与周期长度的变化关系Fig.4 Thermal boundary resistance as a function period length for Si/Ge interface nearest to the hot bath nearest to the hot bath
平均温度在300K到800K之间时,周期长度为10UC的Si/Ge超晶格薄膜界面热阻模拟结果如图6所示。从图中可以明显看出不同温度下薄膜的界面热阻也是不同的,随着温度的逐渐升高,界面热阻越来越小。图中比较了分子动力学模拟、散射失配理论(Diffuse Mismateh Model,DMM)研究[14,15]以及实验数据[16]三种不同方法的计算结果,可以看出他们符合得比较好,变化趋势大致相同。因为实验过程中试样的误差以及DMM理论本身的适用条件限制,二者得到的界面热阻结果比本工作利用分子动力学模拟结果略大。界面热阻随温度升高而减小的原因主要是因为温度的升高使界面处发生非弹性散射的概率增加。在高温下界面处的高频声子只能发生非弹性散射,转化为低频声子才可以传递能量。因此声子的非弹性散射增加了界面的热传导能力,界面热阻也随之下降[7]。
4 结论
(1)受界面热阻机制的影响,在超晶格导热区域的界面处会发生温度的突变,并且在最靠近高温热浴的界面温度突变最为明显。因此,最靠近高温热浴的界面热阻对整个结构的热传导能力起着决定性作用。
(2)界面热阻会随超晶格结构周期长度的增大而逐渐减小,超晶格结构的导热能力会随之相应提高。
(3)随着温度的逐渐升高,界面热阻会越来越小。这与声子在高温下发生非弹性散射概率的增加有关。
[1]吴勇华,杨决宽,陈云飞,等.超晶格薄膜热传导的分子动力学模拟[J].东南大学学报,2003,33(4):468 -470.
[2]吴国强,孔宪仁,孙兆伟,等.单晶硅薄膜法向热导率的分子动力学模拟[J].哈尔滨工业大学学报.2007,39(9):1366-1369.
[3]SHIGEO M.Molecular dynamic method for microscale heat transfer[J].Advances in Numerical Heat Transfer,2000,2(6):189-226.
[4]SRINIVASAN S,MILLER R S.On parallel nonequilibrium molecular dynamics simulation of heat conduction in heterogeneous materials with three-body potentials:Si/Ge superlattice[J].Number Heat Transfer(B),2007,52:297 -321.
[5]MAITI A,MAHAN G D,PANTELIDES S T.Dynamical simulations of nonequilibrium processes—heat flow and the kapitza resistance across grain boundaries[J].Solid Communications,1997,102(7):17-21.
[6]MARUYAMA S,KIMURA T.A study on thermal resistance over a solid-liquid interface by molecular dynamics method[J].Thermal Science Engineering,1999,7:63-68
[7]TWU C J,HO J R.Molecular dynamics study of energy flow an the kapitza conductance across an interface with imperfection formed by two dielectric thin films[J].Phys Rev(B),2003,67(20):205422
[8]李博翰,江建军,朱玲,等.硅锗超晶格薄膜界面热传导的分子动力学模拟[J].功能材料与器件学报,2007,13(3):293-296.
[9]SCHELLING P K,PHILLPOT S R,KEBLINSKI P.Comparison of atomic-level simulation methods for computing thermal conductivity [J].Phys Rev(B),2002,65(14):144306.
[10]STILLINGER F,WEBER T.Computer simulation of local order in con densed phases of Silicon[J].Phy Rev(B),1985,31:5262-5271.
[11]DING K,ANDERSEN H C.Molecular-dynamics simulation of amorphous germanium[J].Phys Rev(B),1986,34:6987-6991.
[12]LANDRY E S,MCGAUGHEY A J H.Thermal boundary resistance predictions from molecular dynamics simulations and theoretical calculations[J].Phys Rev(B),2009,80:165304.
[13]ABRAMSON A R,TIEN C L,MAJUMDAR A.Interface and strain effects on the thermal conductivity of heterostructures:a molecular dynamics study[J].J Heat Transfer,2002,124:963 -967.
[14]SWARTZ E T,POHLR O,Thermal boundary resistance[J].Rev Modern Phys,1989,61:605 -668.
[15]PRASHER R S,PHELAN P E.A scattering-mediated acoustic mismatch model for the prediction of thermal boundary resistance[J].J Heat Transfer,2001,123:105-112.
[16]BORCA T,LIU W,LIU J,et al.Thermal conductivity of symmetrically strained Si/Ge superlattices[J].Superlattices Microstruct,2000,28:199 -206.
