具有连续分布时滞的二阶中立型方程的振动性

赵嬛嬛，刘有军

（山西大同大学数学与计算机科学学院，山西大同 037009）

具有连续分布时滞的二阶中立型方程的振动性

赵嬛嬛，刘有军

（山西大同大学数学与计算机科学学院，山西大同 037009）

考虑一类具有连续分布时滞的二阶非线性中立型方程，获得了其所有解振动的充分条件。

中立型；振动性；连续分布时滞

近来，人们对具有连续分布时滞微分方程的讨论很多，得到了一些好的结果，见文献［1-6］。本文在文献［1］的基础上讨论了一类具连续分布滞量的二阶非线性中立型泛函微分方程有

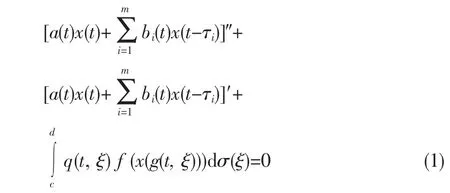
解的振动性问题。

在本文讨论中始终假设下列条件成立：

（H2）g（t，ξ）∈C（［t0，+∞）×［c，d］，R+）；

（H3）σ（ξ）∈C（［c，d］，R），且σ（ξ）关于ξ非减；方程（1）中的积分是Stieltjes积分。

若方程（1）的一个解有任意大的零点，则称其为方程（1）的振动解；否则称为非振动解。

本文的目的是给出方程（1）在一定条件下所有解振动的准则。

且

则方程（1）的所有解振动。

证明 设x（t）是方程（1）的非振动解，不妨设x（t）＞0，t≥t0.令

x（t-τi）＞0，x（g（t，ξ））＞0，t≥t1，ξ∈［a，b］，

显然有

由（5）得，

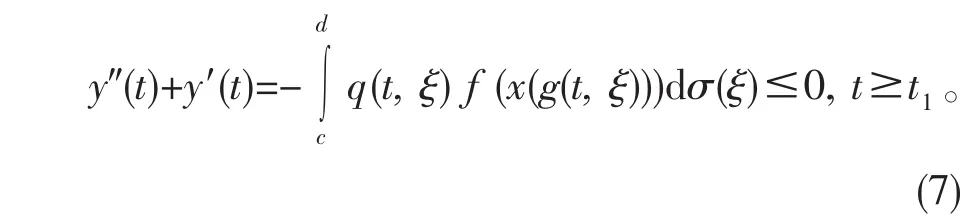
即有

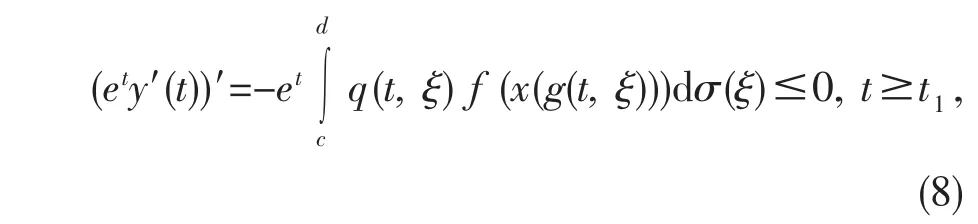
所以ety′（t）在［t1，+∞）上单调减少，从而y′（t）单调减少，即y″（t）≤0，t≥t1事实上，对∀α＜β，eβy′（β）≤eαy′（α），有y′（β）≤eα-βy′（α）≤y′（α）。

下面证明y′（t）＞0，t≥t1。若不成立，则存在T≥t1使y′（T）＜0，由y′（t）是单调减少函数可得

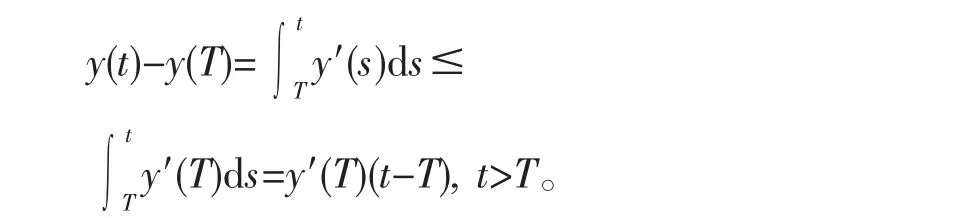
由（3）式，我们有

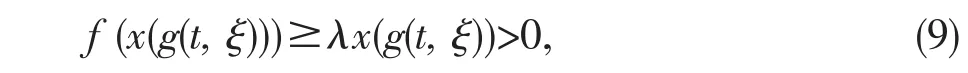
进一步有

注意到y（t）≥x（t），得

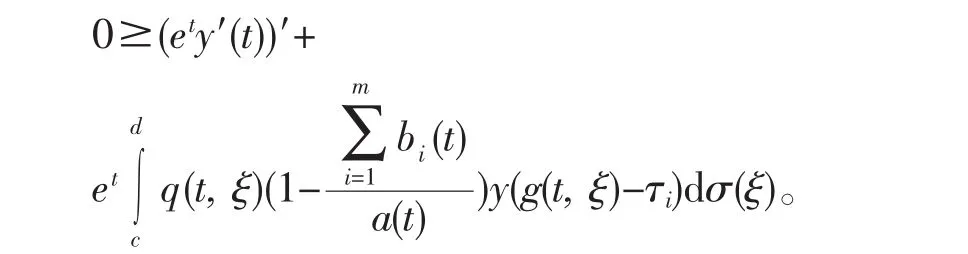
因y（t）在［t1，+∞）上为增函数，可得

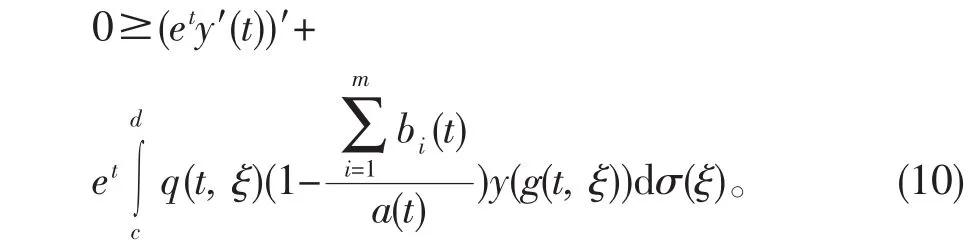
选取常数M＞0，使得y（M）＞0，由假设条件（H2）知存在t2≥t1，使得g（t，ξ）＞M，t2≥t1，再由y′（t）≥0，得y（g（t，ξ））≥y（M）。

从而有（ety′（t））′+

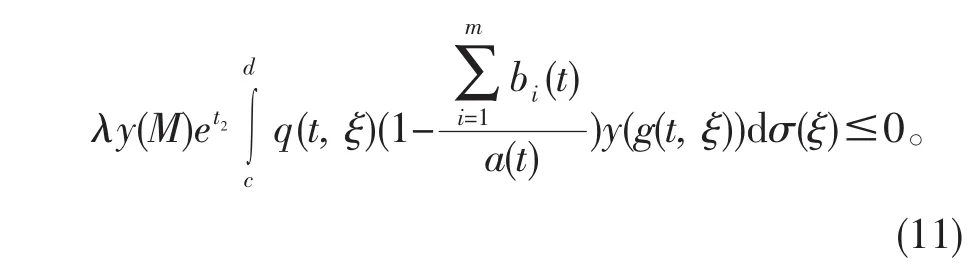
对上不等式从t2到t积分，得

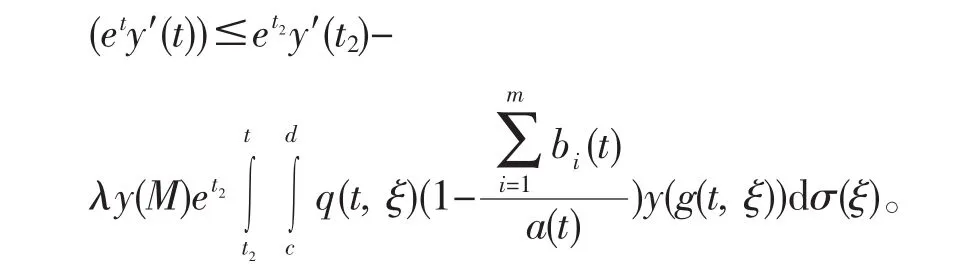
即

这与（4）矛盾。

若x（t）＜0，则可作变换z（t）＝-x（t），则z（t）也满足方程（1）。亦可推出矛盾，定理证毕。

注：特别地，当a（t）≡1，m＝1时，就得到了文献［1］中的结果。因此，本文结果更具有一般性，适用范围更广。

［1］林文贤.具连续分布滞量的二阶中立型方程的振动性定理［J］.应用泛函分析学报，2003，5（2），174-177.

［2］Dahiya R S.Oscillatory Behavior of n-Order Neutral Differential Equtions with Continuous Deviating Arguments［J］.Mathematical and Comfuter Modelling.2004（40）：1131-1139.

［3］张立琴，傅希林.具连续分布滞量的非线性双曲偏微分方程解的振动准则［J］.数学物理学报，1996，16（s1）：12-15.

［4］李伟年，崔宝同.具连续分布滞量的抛物方程解的振动性［J］.山西大学学报：自然科学版，1999，22（2）：8-11.

［5］傅希林.具连续分布型滞量的二阶中立型泛函微分方程的渐近性［J］.数学物理学报，1991，11（3）：24-28.

［6］罗李平.具连续分布滞量的非线性抛物型偏微分方程的振动准则［J］.海军工程大学学报，2007，19（2）：15-19.

〔编辑 高海〕

Oscillatory Criteria for a Class of Second Order Neutral Equations with Continuous Distributed Delay

ZHAO Huan-huan，LIU You-jun
（School of Mathematics and Computer Sciences，Shanxi Datong University，Datong Shanxi，037009）

This paper consider a class of second order nonlinear neutral differential equation with continuous distributed delay，sufficient conditions of the oscillation for solutions are obtained.

neutral；oscillation；distributed delay

O175.14

A

1674-0874（2011）01-0001-02

2010-08-20

山西省自然科学基金资助项目［2008011002-1］；山西大同大学青年科研基金资助项目［2008Q7］

赵嬛嬛（1979-），女，山西左云人，硕士，讲师，研究方向：微分方程。