汉诺塔问题的非递归算法设计及可视化实现＊

彭 伟

（武汉城市职业学院，湖北武汉 430064）

汉诺塔游戏最早于19世纪出现在欧洲，它展示了一项正在婆罗门寺庙进行的任务：在创世之初，牧师被授予一个铜盘，上面有3根钻石针，在第1根针上叠放着64个碟片，每一个都比它下面的稍小一些，这位牧师被安排了一项任务，那就是将所有的碟片从第1根针移到第3根针，但要遵循的规则是：一次只能移动一个碟片，并且不允许将任何一个碟片放在比它小的碟片上面。牧师被告知：当他将64个碟片移动到第3根针时，世界末日将会到来。

编写程序算法求解汉诺塔问题是一项很有趣的任务，特别是其算法设计思想对很多类似问题的求解都有借鉴作用。本文将分别讨论解决该问题的经典递归算法及该算法与二叉树结构的内在关系，进一步研究解决该问题的非递归算法，最后在可视化程序开发平台上实现移动过程的动态模拟。

1 汉诺塔问题递归算法及二叉树分析

各种版本的《数据结构》、《计算机算法》等教材都详细讲述了如何使用递归算法解决该问题。以将N个碟片由第1针移到第3针为例，算法基本思想表述如下：

（1）首先将上面的N－1片移到第2针；

（2）再将第N片移到第3针；

（3）将第2针上共N－1片移到第3针。

对于第2步中暂时回避了的N－1片的移动问题，它将继续遵循同样的移动思路。

上述问题的求解过程体现了递归算法思想，对复杂的问题分而治之，将工作分解成越来越小的部分，使得每一个部分都比原始问题易于解决。

Hanoi问题的经典递归算法如下：

其中N为碟片数，s、e为起／止针编号，t为所借助的针编号。

观察该算法，很容易发现它与二叉树的中序遍历算法非常相似：

受版面局限，本文中包括上述代码在内的所有代码均未使用标准缩进风格编写。上述两段代码解决的问题毫不相关，但在代码结构、语句顺序上却极其相似。对于4个碟片的汉诺塔问题，可以很容易地使用递归树分析工具对算法进行分析，得出程序执行的清晰路线图。

Hanoi的递归树如图1所示，按照上述算法，实际应该还有一层，但由于该层遇到N＝0而立即返回，未执行任何移动操作，故略去。程序的执行路线如图1中带箭头的线条所示，可以设想，图1中每个圆圈内包含了上述函数的完整“代码副本”，它们由三个部分构成：

第①部分，即 Move（N–1，s，t，e），形成向左的调用（递进调用）；

第②部分，即printf（"%d，%d－＞%d.＼n"，N，s，e），它处于两个递归调用语句的中间，图中反向箭头指向该部分，它将产生一次打印输出（一次回归）；

第③部分，即 Move（N–1，t，e，s），形成向右的调用（递进调用）。

所绘制的“递归树”清晰地呈现出“二叉树”结构特征，其中“向下箭头”为“递进”调用，“向上箭头”则为一次“回归”，整个递归过程由此构成。

考察“二叉递归树”可知，Hanoi算法的执行路线正好是二叉树的Mid＿Order算法路线，即它们走的都是中序遍历路线。而且，Hanoi的递归树还是一棵满二叉树，树的高度等于总碟片数N。类似地，八皇后问题的递归树一定是八叉树，只不过它不一定是满的。由该二叉树可以很容易计算出解决4个碟片问题的总移动次数，由于每一个结点中含有一次打印（未画出的一层中不含有任何操作），对应于总共N个碟片的N层满二叉树，其结点总数为：2N–1，可见，4个碟片的汉诺塔问题共需要24–1＝15次移动。

回到最初的64个碟片的汉诺塔问题，显然共需要264–1次移动，假定牧师每秒移动一个碟片，则共需时间约为：5×1011年。天文学家估算的宇宙年龄约为2×1010年，那么解决汉诺塔问题所花的时间将是宇宙年龄的25倍，看来汉诺塔的预言并非完全是虚妄的。

2 非递归算法的设计分析

汉诺塔问题的递归算法非常简洁，但是要直接回答问题：N片的汉诺塔问题中第i步应该移动哪一片？递归算法显然效率低下，因为它必须一直递归到二叉树中的相应结点位置时，才能回答这一问题。

如果能找出某种解决方法，仅仅给出变量i即可知道应该移动谁及如何移动，那么整个算法中通过2N－1次循环即可打印出所有移动步骤。

下面进一步考察分析Hannio问题二叉递归树中各结点的碟片移动规律，研究汉诺塔问题的非递归算法。

整个非递归算法要解决的问题有两个：

（1）第i步（即结点i）应移动哪一碟片

首先约定，将二叉树最底层编号设为1，依次向上一直到根结点，分别为2、3、4层（这与数据结构教材中定义的一般顺序相反），层的编号用变量Ln（Level Number）表示。二叉树中的各结点则按中序遍历序列逐一编号，分别为1～15。考察图1所示二叉树发现：

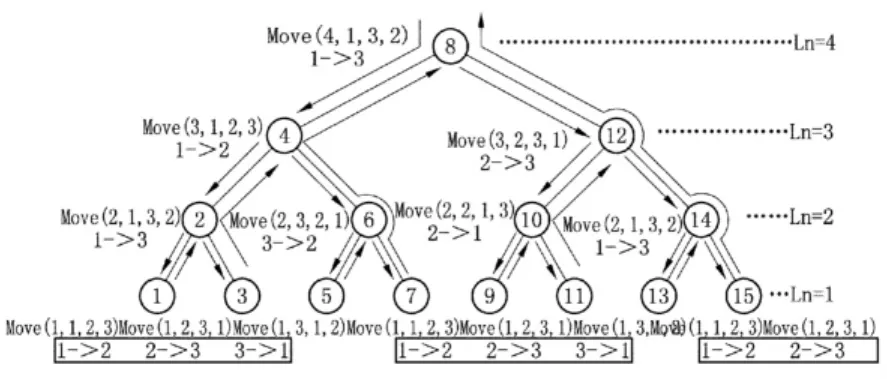
图1 用二叉递归树跟踪分析求解汉诺塔问题的递归算法

（Ⅰ）第Ln层移动的碟片固定为Ln号碟片，即同一层总是处理同一片碟片。

（Ⅱ）第Ln层各结点编号的最大公约数为2LN－1。

例如1、2、3、4层内各结点编号的最大公约数分别为1、2、4、8，每上升一层，最大公约数递增一倍。它们实际上就是各层二叉树最左边分支的结点编号。

显然，假设当前要执行第i步移动（对应于结点i），由结点编号i求出层号Ln，也就得到了第i步要移动的碟片号。根据所分析得出的规律，可通过如下方法求取Ln：

例如：i＝12，先假定它所在层为Ln＝1，然后将i／2，除尽，故得Ln＝2；再将i／4，又除尽，故得Ln＝3；继续将i／8时，不能除尽，故得Ln最后为3。

对应的C程序代码实现为：

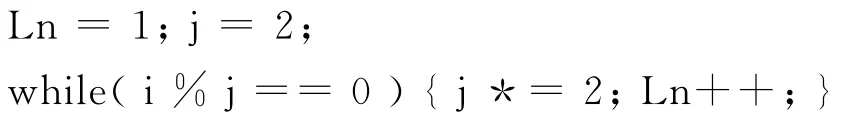
（2）如何确定起、止针编号

得出根据i值获取当前待移动碟片号的算法以后，还需要进一步研究找出第i步所移动的碟片的起始位置和目标位置。进一步考察二叉树可知：

（Ⅰ）各层的第一个结点移动碟片时，起始针编号均为1，因为对于任意规模的问题，最初所有碟片都在1针上，目标针是2或3；

（Ⅱ）当前树的层数N（即总碟片数）与结点i所在的层数Ln同奇或同偶时，目的针为3，否则必为2。

（Ⅲ）树中每一层存在固定的移动回路。

对于图1所示二叉递归树中的第1层，它所移动的都是第1片，其中前三次移动为：

这一序列刚好形成一个有3个顶点3条边的回路，碟片从第1针出发，走过另两针后回到起点，后面接着的三个结点将以同样的回路移动。

增加问题的规模，例如N＝5、6，可以清晰地观察到其对应的递归二叉树中每一层（包括最下层）都具有固定的移动回路，且周期性重复。可见，每层移动的是同一碟片，且同一碟片的移动总是按固定的回路重复轮转。

由上述三个特征可知，在已经通过i值得出层编号Ln，也就是待移动碟片号以后，根据它在当前层内部的横向编号，可推导出它的原始位置与目标位置。

假设Sn为第i个结点在Ln层内的横向编号，例如第1层内结点横向编号范围为1～8，第11号结点处于第1层，它在该层内的横向编号为6。

由于第Ln层内结点的编号间隔为2Ln，例如第2层内结点的编号间隔为22＝4，编号分别为2、6、10、14。

根据这一特点可得层内横向编号公式：

用C实现四舍五入函数ROUND时有：

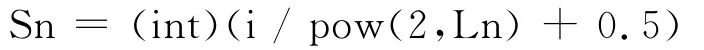
例如：Sn＝（int）（11／21＋0.5）＝6，即11号编点在其所在层（第1层）内横向编号为6。

由i值已经可以得出当前移动的Ln号碟片在Ln层横向编号为Sn，由于横向编号为1的起始针编号必为1，且根据同奇／同偶的特征可得到周期出现的移动回路。

故接着仅仅还需要得出Sn在当前层周期为3的移动回路内部的序号，为解决这个问题，可定义变量p，其中1≤p≤3。有：

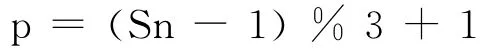
例如：第11号结点（i＝11）在第1层内的横向编号为Sn＝6，循环移动回路为：

它是第二个循环中的第3步，即p＝3。

由于循环回路中第1步移动为“1→2”，则第二步移动必定为：

由“2→3”又可以得出第三步移动为：

又如：i＝15，得p＝2，故移动必为：

可见，由结点号（即步骤号）i可得出层编号Ln，也就是将移动的碟号；同时，由i还可得出它在层中的横向编号Sn，从而得出它在回路中所处的移动步骤号p（1≤p≤3）。而任一回路第1步移动的起／止针编号为（s，d），根据（Ⅰ）与（Ⅱ）可知它们分别为：

故而由p可得出横向编号为Sn的结点的移动方法，也就是结点i的移动方法。问题最终得解。

基于对二叉递归树各结点对应的碟片移动情况的深入分析及研究结果，所得出的不使用堆栈技术的汉诺塔问题非递归算法C程序代码如下：

3 两种算法的可视化设计与模拟移动

为了更直观的验证显示汉诺塔问题的递归算法及由二叉递归树研究分析所得出的非递归算法的运行效果，可考虑选择基于.NET开发平台，用VB.NET或C＃.NET开发可视化程序，实现整个移动过程的动态模拟。所设计的可视化模拟动态移动程序界面如图2所示，其中：

（Ⅰ）用树形视图组件（TreeView）显示的递归树窗口中，每一结点名称前形如“（？）”的数值为结点编号，与图1对应。

（Ⅱ）移动过程窗口用于顺序显示每一步移动的碟片号及起／止针名称（A／B／C）。

（Ⅲ）碟片的动态移动过程在最上面的图形窗口用Graphics绘图对象显示。

限于篇幅，本文仅列出两种算法的VB.NET版相关核心代码，更完整的 WinForm程序可由读者自行完善。

图2 递归与非递归算法运行测试及可视化移动模拟

（1）相关变量定义

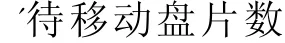
（2）汉诺塔的递归函数

（3）汉诺塔的非递归函数

（4）模拟碟片移动过程的函数

4 结 语

本文结合递归树分析工具，对解决汉诺塔问题的经典递归算法进行分析研究，并基于对二叉递归树的深入分析研究结论，得出了未使用堆栈的非递归解法，并在.NET可视化程序设计平台对两种算法均进行了模拟移动验证，取得了所预期的理想效果。

1 Robert Kruse，CL Tondo，Bruce Leung.DATA STRUCTURE ＆ PROGRAM DESIGN IN C［M］.PRENTICE HALL，2001

2（美）维斯.数据结构与算法分析C＋＋描述（第三版）［M］.人民邮电出版社，2007

3（美）麦克米兰.数据结构与算法（C＃语言版［M］.清华大学出版社，2009

4（美）萨尼.数据结构、算法与应用：C＋＋语言描术［M］.机械工业出版社，2005

5 余祥宣，崔国华，邹海明.计算机算法基础（第二版）［M］.华中科技大学出版社，2000