环口板加固Y型方钢管节点在轴压作用下极限承载力的有限元分析

王学高， 邵永波

(烟台大学 土木工程学院，山东 烟台 264005)

钢管结构在力学性能和施工性能等方面具有一系列的优点，因此被广泛应用于工程建设领域，如冶金、造船、海洋平台、大跨空间结构和桥梁结构中。在这些结构中，一个或几个小的空心钢管直接焊接到大的空心钢管表面构成管节点。管径较小的钢管称为支管，管径较大的钢管称为主管。由于主管贯通以及支管主要承受轴向力的作用，主管在节点部位必然承受径向的作用力。对于空心薄壁的主管来说，它在径向的刚度往往远小于支管的轴向刚度，所以主管表面靠近焊缝部位是管节点最常见的破坏部位。

为了提高管节点的承载力，加固措施很有必要。已经有很多学者对管节点加固方法进行了研究，归纳起来，主要有内置加劲环加固、内置插板加固、主管壁加厚加固、垫板加固、环口板加固等方法。文献［1～4］分别通过试验测试和有限元分析的方法研究了内置加劲环对提高管节点承载力的有效性。文献［5，6］研究了内置插板对管节点承载力的影响。文献［7］研究了将节点附近的主管管壁加厚对承载力的影响。这三种加固方法均属于主管内部加固方式，不影响节点的外观，但是操作复杂，施工难度较大，在焊接上很难保证质量。垫板加固在节点发生破坏时可以有效地保护主管，国内外也进行了大量的研究工作［8～10］。

环口板加固是一种新颖有效的加固措施，因为这种加固方式可以在管节点的使用期间采用，而其他的加固方式只能用在管节点的设计阶段。新加坡国立大学的Choo等人首先提出环口板加固方法，并对该方法进行了一系列试验测试和有限元分析，结果发现环口板加固可以显著地提高管节点的承载力［11～13］。

本文对环口板加固Y型方钢管节点进行有限元分析。

1 有限元模型

环口板加固方钢管节点中，先将支管直接焊接在主管表面上，然后将环口板焊接在支管和主管上。图1是环口板加固Y型方钢管节点的几何形状示意图。

在分析管节点时常采用几个无量纲参数，如支管宽度和主管的宽度比β=d1/d0，主管的宽厚比2γ=d0/t0，环口板厚度与主管壁厚比τc=tc/t0，环口板宽度与支管宽度比lw/d1。

在对管节点进行有限元建模分析时，主要有两种单元，即实体单元和壳单元。实体单元能较为准确地模拟节点试件的受力情况，得出应力在管壁厚度方向上的变化情况。但由于划分的单元数较多，计算时间较长。壳单元便于网格划分，单元数目少，节省计算资源。但它忽略了应力在管壁厚度方向上的变化，通常也会弱化节点的刚度尤其是主管的径向刚度，使节点的极限承载力计算结果偏于保守。因此，在满足计算机性能的前提下，本文在进行有限元模拟时均采用实体单元。

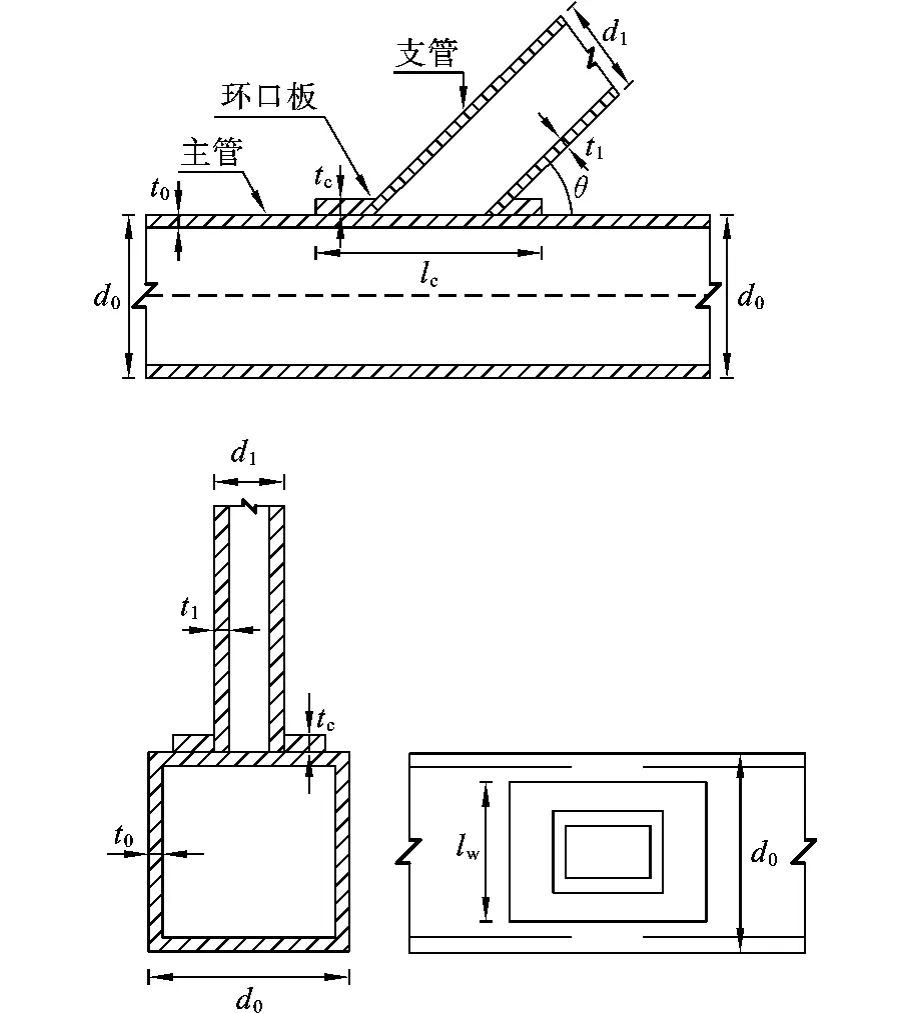
图1 环口板加固Y型方钢管节点

在有限元分析中，采用理想弹塑性的材料模型，主管、支管和环口板的钢材屈服强度均为345 MPa，弹性模量和泊松比分别为160×103MPa和0.3。

采用有限元软件ANSYS对管节点进行建模分析。单元采用SOLID45实体单元，此单元为8节点6面体一次单元。在进行网格划分时，对网格的密度进行控制，主管与支管交界部分及环口板划分的单元尺寸较小，节点其余部分的单元尺寸则较大。采用此网格划分方法得到的加固管节点如图2所示。采用TARGE170和CONTA173接触单元在环口板的底面与主管上表面之间建立接触以模拟环口板与主管的接触行为。

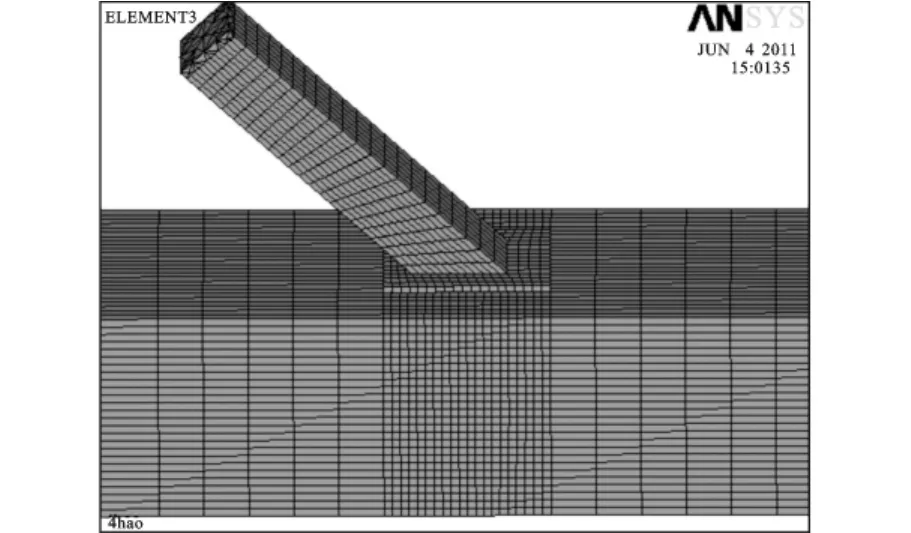
图2 环口板加固Y型节点的网格划分

2 环口板加固Y型节点承载力分析

2.1 节点模型

为了研究环口板加固对节点承载力的影响，对环口板加固节点进行了分析。分析中共考虑了4个参数，包括支管宽度与主管宽度比β，主管宽度与主管壁厚的比2γ，环口板厚度与主管管壁厚之比τc和环口板宽度与支管宽度之比lw/d1。对于所有有限元模型，主管与支管的管壁厚度固定为10 mm，主管长为2.0 m，支管长为0.4 m。Y节点主管与支管的夹角θ为45°，环口板长度lc=lw/sinθ。表1为加固Y型节点的参数，在有限元分析时，每一个加固节点分别对应一个未加固节点，模型1至13与模型18对应的未加固节点的尺寸是一样的。

表1 未加固Y型节点的参数

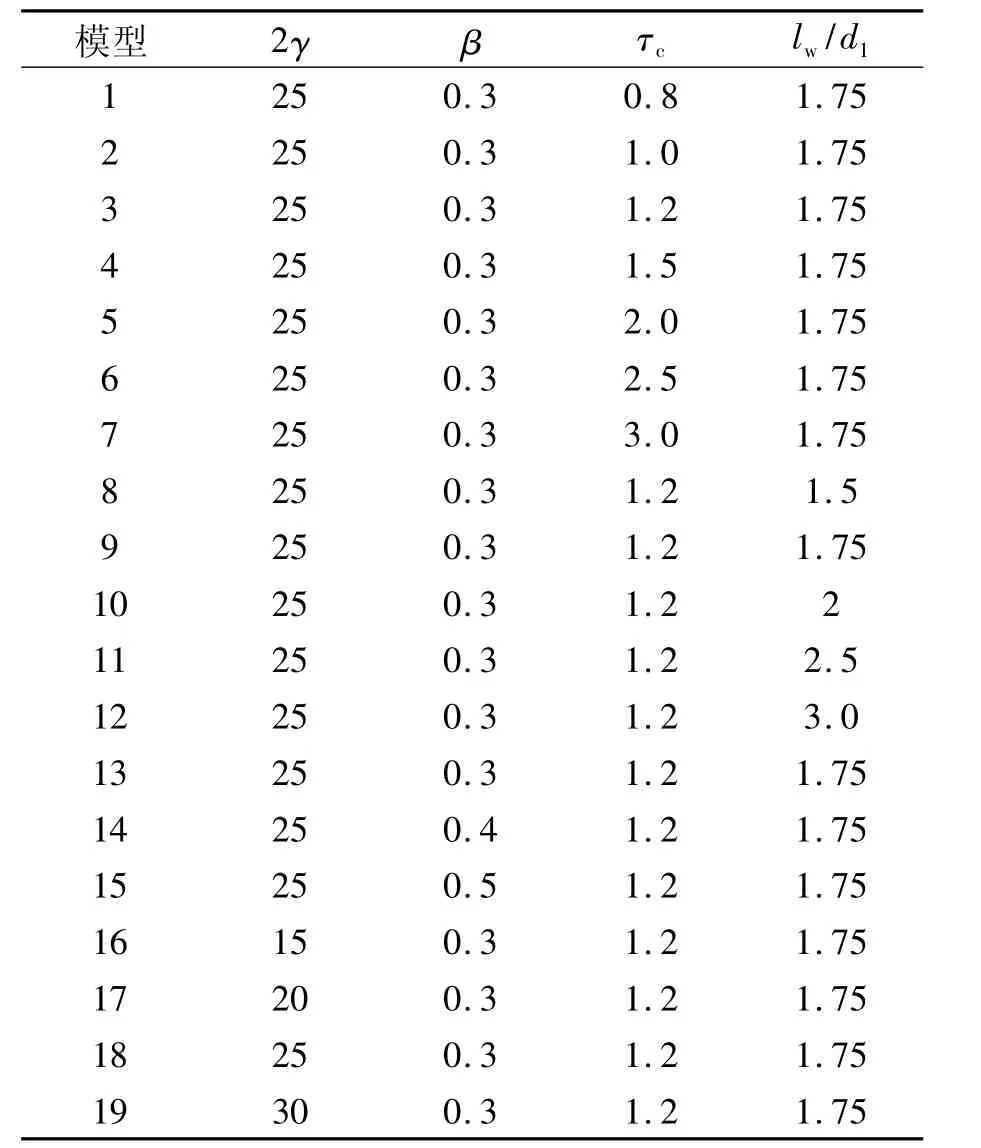
表2 加固Y型节点的参数

在进行有限元模拟时，主管采用一端铰接，一端滑动支座的边界条件设置。通过对支管端部自由度的限制使支管只发生轴向的位移。加载方式采用位移控制，通过控制支管端部发生轴向位移对模型进行加载。

2.2 环口板加固与未加固节点极限承载力比较

定义极限承载力的方法有好几种，本文采用其中最常用的两种定义方法。第一种定义方法是将节点的荷载-变形曲线最高点对应的荷载值作为节点的极限承载力。然而，如果荷载-变形曲线没有明显的下降段，这种定义方式是不适用的。另一种方法考虑了主管在焊缝处的局部变形，将变形值为主管宽度的3%时对应的荷载值作为节点的极限承载力。图3为模型4环口板加固节点与对应的未加固节点的极限承载力比较，可以看出环口板加固节点的承载能力比未加固节点的承载能力提高61.2%，表2为环口板加固节点与未加固节点的的极限承载力比较，环口板加固节点的承载力与相对应的未加固节点的承载力相比，均有较大的提高。说明环口板加固可以用于Y型方钢管节点，并显著提高节点的极限承载力。

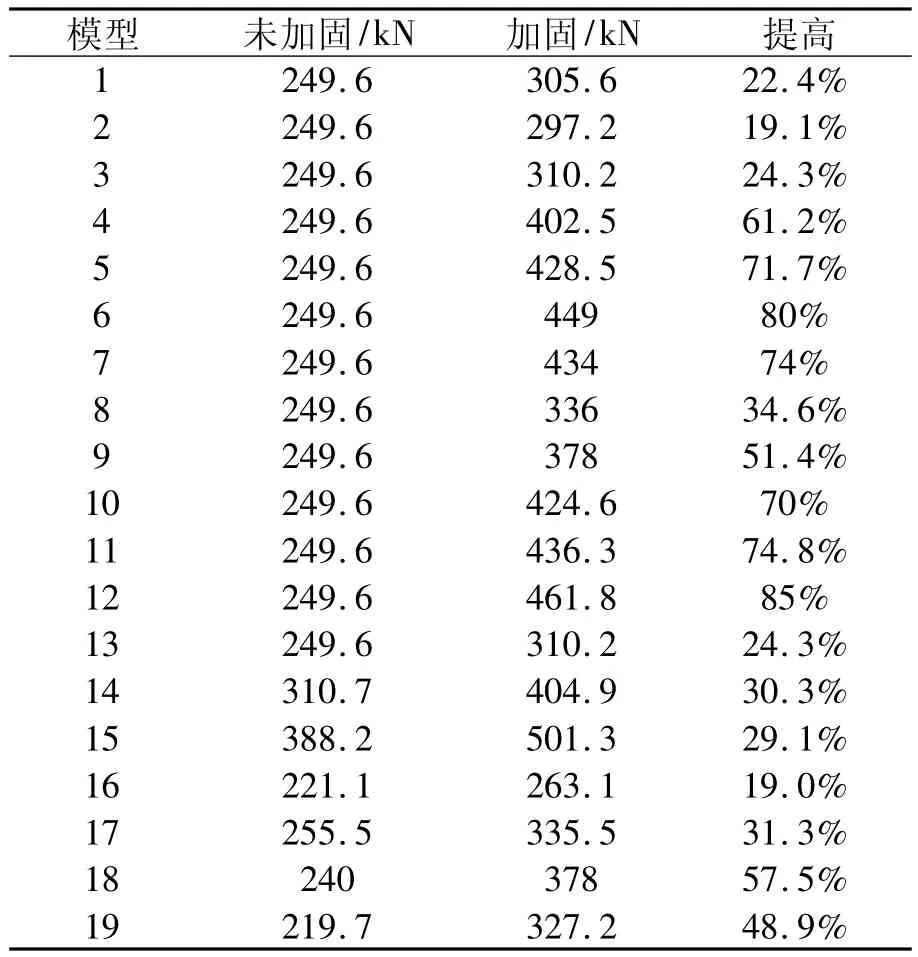
表3 加固与未加固节点极限承载力比较

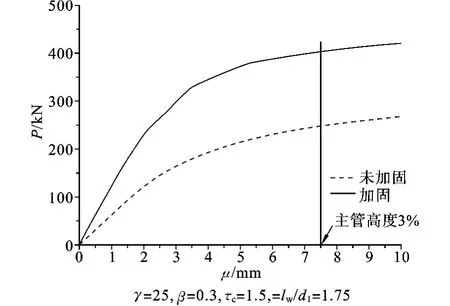
图3 2γ =25，β=0.3，τc=1.5，lw/d1=1.75

2.3 环口板厚度对极限承载力的影响

图4为环口板厚度对极限承载力的影响。图4中对于同一组模型，增大环口板的厚度对节点极限承载能力的提高非常显著，当τc为2.5时，节点的极限承载力提高非常明显，提高约80%。为3.0时，环口板承载力的提高效果为74%。所以建议环口板的厚度不宜超过主管管壁厚度的2.5倍。

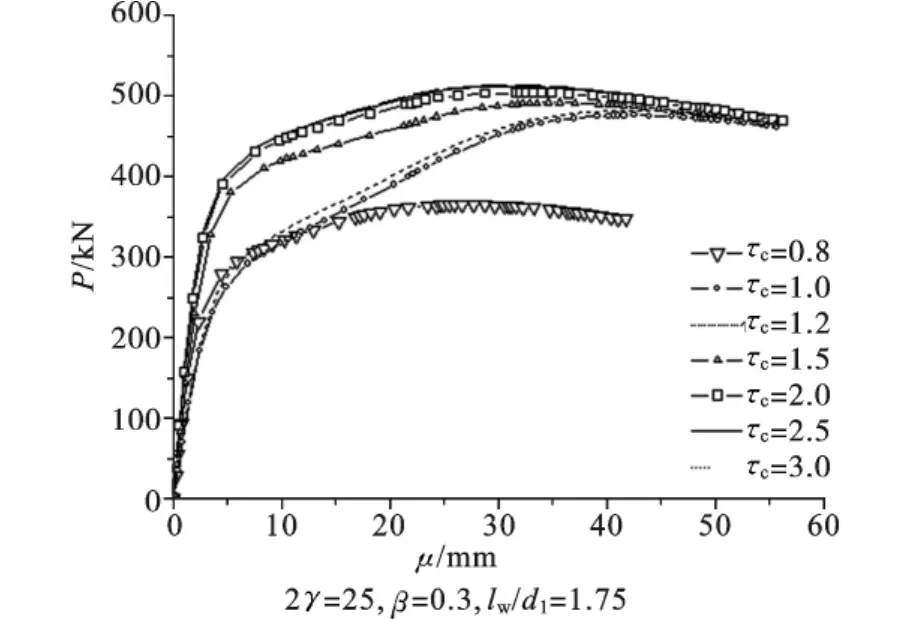
图4 环口板厚度对承载力的影响

2.4 其他参数对极限承载力的影响

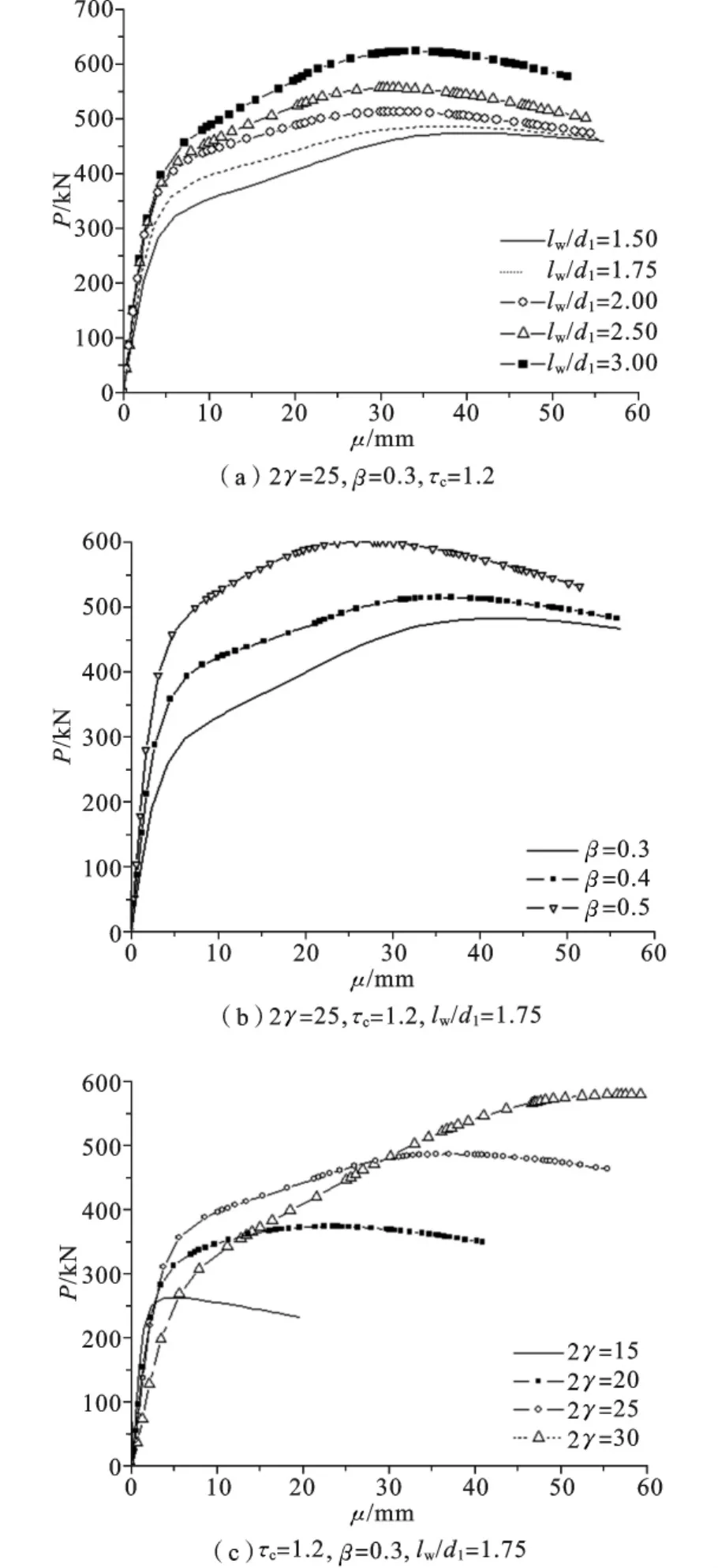
图5 环口板长度对承载力的影响

从图5(a)可以看出，节点的承载力随着lw/d1的增大而提高，lw/d1为2.0时，环口板加固节点的极限承载力提高约70%，当lw/d1达到2.5时极限承载力提高约74.8%，当lw/d1达到3.0时极限承载力提高约85%。因为lw/d1再增大的话，环口板宽度就会超过主管的宽度，所以建议环口板宽度不宜超过支管宽度的3.0倍。从图5(b)可以看出，节点的承载力随着β的增大而提高。但β的值不宜太大，因为β达到0.6时，环口板宽度就会超过主管的宽度，所以建议β的取值不宜超过0.5。图5(c)中，节点的承载力随着2γ的增大而提高，但当2γ达到30时承载力下降，因为主管径厚比2γ较大，而β较小时，主管上翼缘板承受支管传来的横向荷载并破坏，主管侧壁发生局部屈曲破坏，所以承载力下降，可以在主管两侧面焊接一块加强板，提高主管的剪切强度，防止主管侧壁屈曲。

图6 节点的破坏模式

3 破坏模态

未加固节点的破坏为主支管交汇处的主管冲剪破坏如图6(a)，当τc为1.2时即环口板厚度较小时，采用环口板加固后的节点为环口板的屈服破坏如图6(b)。当τc为2.5时即环口板厚度较大时，采用环口板加固后的节点为环口板外围与主管相交处的屈服破坏如图6(c)。

4 结论

(1)环口板加固Y型管节点可以显著提高节点的极限承载力。

(2)节点的承载力随着lw/d1的增大而提高，建议环口板宽度不宜超过支管宽度的3.0倍。

(3)节点的承载力随着τc的增大而提高，但环口板加固厚度不宜太大，建议环口板厚度不超过主管厚度的2.5倍。

［1］Ramachandra Murthy D S，Madhava Rao A G，Gandhi G，et al.Structural efficiency of internally ring-stiffened steel tubular joints［J］.Journal of Structural Engineering，ASCE，1992，118(11):3016-3035.

［2］Thandavamoorthy T S，Madhava Rao A G，Santhakumar A R.Behavior of internally ring-stiffened joints of offshore platforms［J］.Journal of Structural Engineering，ASCE，1999，125(1):1348-1352.

［3］Lee M M K，Llewelyn-Parry A.Strength of ring-stiffened tubular T-joints in offshore structures—a numerical parametric study［J］.Journal of Constructional Steel Research，1999，51:239-264.

［4］Lee M M K，Llewelyn-Parry A.Offshore tubular T-joints reinforced with internal plain annular ring stiffeners［J］.Journal of Structural Engineering，ASCE，2004，130(6):942-951.

［5］王 阁，张季超.内置加强板空间相贯圆钢管节点在广东科学中心工程中的应用研究［J］.工业建筑，2007，37(10):93-97.

［6］李 涛，邵永波，张季超.内置横向插板加强型管节点静力强度研究［J］.钢结构，2009，24(123):25-29.

［7］Shao Yongbo.Study on reinforcing methods for welded tubular joints structures［J］.Journal of Yantai University(Natural Science and Engineering Edition)，2009，22(4):312-320.

［8］Fung T C，Chan T K，Soh C K.Ultimate capacity of doubler plate-reinforced tubular joints［J］.Journal of Structural Engineering，ASCE，1999，125(8):891-899.

［9］Fung T C，Soh C K，Chan T K，et al.Stress concentration factors of doubler plate reinforced tubular joints［J］.Journal of Structural Engineering，ASCE，2002，128(11):1399-1412.

［10］Choo Y S，Liang J X，van der Vegte G J，et al.Static strength of doubler plate reinforced CHS X-joints loaded by in-plane bending［J］.Journal of Constructional Steel Research，2004，60:1725-1744.

［11］Choo Y S，Liang J X，van der Vegte G J，et al.Static strength of collar plate reinforced CHS X-joints loaded by in-plane bending［J］.Journal of Constructional Steel Research，2004，60:1745-1760.

［12］Choo Y S，van der vegte G J，Zettlemoyer N，et al.Static strength of T-joints reinforced with doubler or collar plates.I:experimental investigation［J］.Journal of Structural Engineering，ASCE，2005，131(1):119-128.

［13］van der Vegte G J，Choo Y S，Liang J X，et al.Static strength of T-joints reinforced with doubler or collar plates.II:numerical simulations［J］.Journal of Structural Engineering，ASCE，2005，131(1):129-138.