多结构元多路加权形态边缘检测算法研究

徐美芳

（中北大学信息与通信工程学院，山西太原 030051）

0 引言

边缘检测是图像特征提取与分析理解的基础，其检测质量直接决定后期理解的效果。经典的边缘检测算法大都使用的是局部微分算子如 Sobel、Prewitt、Canny、Laplacian 和Marr-Hildreth等，这些算法简单、易实现且检测速度快，但定位精度差，容易受噪声干扰。利用Canny算子改进的（多结构元）抗噪型数学形态学边缘检测算法对气瓶阀型式试验气密性进行了测试，一定程度上解决了信噪比和单边缘响应两个性能指标之间的矛盾［1］。随着数学形态学、小波变换、神经网络、模糊理论和遗传算法［2-4］等新理论在边缘检测中的应用，新方法不断涌现。但在实际应用中，针对不同的图像仍存在不少缺陷，需要进一步完善。文献［5］在Pal和King算法的基础上，提出了一种改进的图像模糊边缘检测算法。该算法克服了Pal和King算法丢失图像灰度信息的缺陷，显著提高了边缘检测的质量。文献［6］将形态学多结构元与图像边缘进行匹配，提出了3种广义顺序形态边缘检测算子，该边缘检测算子在抑制噪声对图像边缘的影响和保持图像细节方面。以上算法一定程度地抑制噪声和保持边缘细节，但因结构元素的单一在检测各种几何形状的边缘上也存在欠缺。本文参考形态滤波的思想，分多路对图像进行交替形态开、闭操作，并在每一路中采用不同的结构元素，运用改进加权融合算法提取出较理想的边缘图像。

1 抗噪型形态边缘检测算子

对输入图像函数的α-调整式表示为:

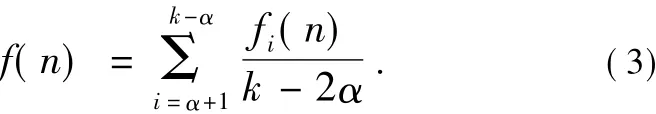
该算法同式（1）形式上非常相近，不同之处在于（2）是通过调整输入图像进行降噪，而前者是通过对原图像平滑滤波来滤除噪声。两者还有一个相同之处，即它们都不是通过形态学固有的性质来滤除噪声，而只是对原图像进行调整和平滑，因此只能说这二者都用到了形态学而并未充分体现出形态学运算本身可以滤除小于结构元素尺度的噪声点的优越性。

抗噪型形态边缘检测算子如下:

上述三式中，抗噪膨胀型形态边缘检测算子OGrad1对正脉冲的响应为零，抗噪腐蚀型边缘检测算子OGrad2对负脉冲的响应为零，抗噪膨胀腐蚀型OGrad3检测算子则对正负脉冲的响应都为零。为了使得对正负脉冲皆有抑制作用，对其进行如下修正:

抗噪膨胀型:

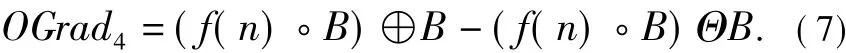
抗噪腐蚀型:

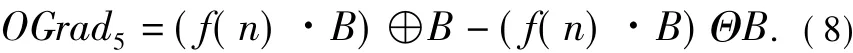
修正后的OGrad4和OGrad5算子对正负脉冲的响应都为零，将其应用于噪声污染图像的边缘检测，可有效滤除噪声。

形态学边缘检测算子中，J.Lee等提出了一种能较强抑制噪声的模糊最小化形态边缘提取算子（Blur-Minimization Edge Detector）也称为BM方法。其算法描述如下:

其中，B（n）是结构元素函数，f（n）是二维输入图像。

Feehs和Aree提出了α-调整边缘检测算子也称为ATM方法（α-Trimmed Morphological Edge Detector）。该方法的主要思想是通过调整对输入图像f（n）进行了α-调整以达到去噪的目的。ATM边缘检测方法检测公式为:

2 改进算法

算法步骤如下:

（1）首先针对某一结构元素{Bi|i=1，2，L4}分A、B两路处理，一路进行开-闭运算，另一路进行闭-开运算。开、闭运算可分别对含噪图像的内外进行滤波达到去除噪声的目的，两种运算都可除去比结构元素小的图像细节，同时保证不产生全局的几何失真。对每一路运算中的每一个结构元素的滤波结果，按以下方法求其最值，得到f'a（n）和f'b（n）。

对开—闭运算结果采用最大值:

对开—闭运算结果采用最小值:

该步骤中，开—闭运算和闭-开运算中不同的形态操作也可以选择为不同的结构元素。

（2）用f'a（n）和f'b（n）分别得到噪声较小的图像，并计算各个结构元素滤波效果的峰值信噪比psnri，i=1，2，L4，根据其比例确定权重:

（3）针对各结构元素再对A路的结果fa'（n）分别进行开启和腐蚀操作;对B路的结果fb'（n）分别进行腐蚀和膨胀操作，求得图像边缘，按照权值ωi进行合成，生成每一路的边缘图像。在该形态操作中，结构元素的选择需要变换尺度和结构，采用不同于上步中的结构元素，目的是进一步去除噪声。

（4）针对各路求得的图像边缘再次进行重构，得到最终的图像边缘。

检测的边缘图像=α+A路+（1-α）×B路，其中，α∈（0，1），可以根据检测出边缘效果和不同的要求进行合理的参数调整。

（5）如果想获取灰度边缘图像，需要对结果图像进行灰度范围的调整，以提高图像的可观性;如果需要获取二值边缘图像，需要根据结果图像求取阈值，进行二值化处理，得到最终的边缘图像。

3 结果分析

分别用含5%椒盐噪声的图像对以上算法进行了实验，并与单一结构元素下的抗噪型形态边缘算子进行检测比较。图1为采用单一结构元素抗噪型形态算子的检测结果，结果表明:噪声已有效滤除，因结构元素选取的不同，得到的实际边缘效果有所不同，在一定程度上保持了图像的边缘细节，但检测的边缘效果各有不同。图2和图3分别为采用多结构元素A、B单路运算的检测结果，其中图2和图3中（a）、

从图1可以看出，采用单一结构元素很难将去噪与边缘保持结合处理。图2和图3显示了结构元素的不同所带来的检测效果的改善，使用多结构元素检测图像可以获得更加清晰和连贯的边缘，对噪声的敏感度也明显降低。图4（a）和（b）中A、B两路的加权边缘图已经取得了良好的边缘细节保持和除噪的效果，图4（c）和（d）采用不同权重合成的结果在细节明晰和降噪有明显优势。

图1 采用单一结构元素抗噪型形态算子的检测结果

图2 采用多结构元素A路运算的检测结果

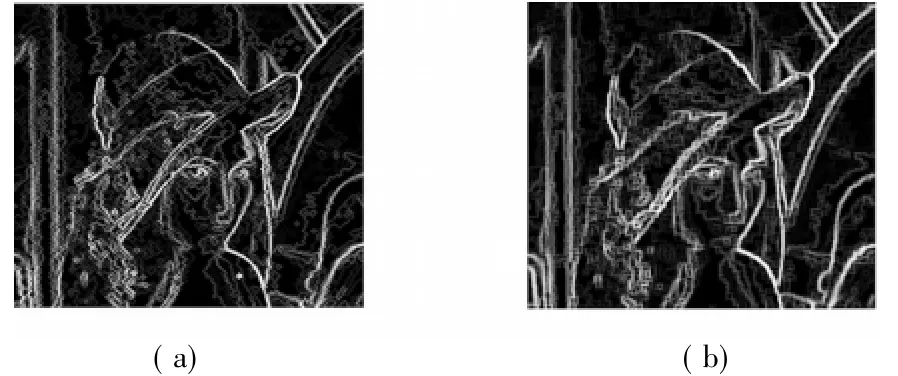
图3 采用多结构元素B路运算的检测结果

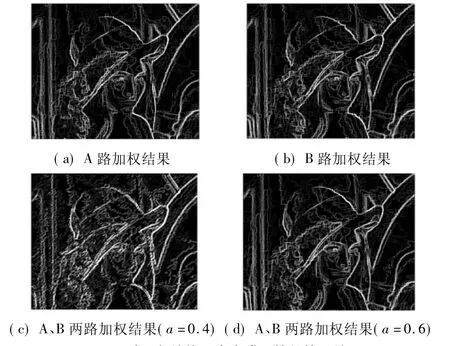
图4 采用多结构元素合成运算的检测结果

4 结论

在抑制噪声对边缘的影响和保持图像的边缘细节上，多结构元素多路合成算法的效果要优于经典的边缘检测算子和单一结构元素抗噪型边缘检测算子，较好地实现了噪声图像的弱边缘检测。其结果的进一步加权与否和加权的系数可以视该二路结果的检测效果而定，在对图像进行开—闭和闭—开运算时也可再采用多尺度方法，效果会更好，但运算复杂度增加。

［1］量慧锋.基于数学形态学的边缘检测算法研究及应用［J］.计算机工程与应用，2009，45（9）:223-226.

［2］Akara Sopharak，Bunyarit Uyyanonvara.Automatic Detection of Diabetic Retinopathy Exudates from Non-dilated Retinal Images Using Mathematical Morphology Methods［J］.Computerized Medical Imaging and Graphics，2008，32:720–727.

［3］王海虹.基于小波变换和数学形态学的激光成像雷达图像边缘检测［J］.中国激光，2008，35（6）:903-908.

［4］Olivier Strauss，Frédéric Comby.Variable Structuring Element Based Fuzzy Morphological Operations for Single Viewpoint Omnidirectional Images［J］.Pattern Recognition，2007，40:3578 – 3596.

［5］杨勇，黄淑英.一种改进的Pal和King模糊边缘检测算法［J］.仪器仪表学报，2008，29（9）:1918-1922.

［6］迟健男，方帅，徐心和，等.基于多结构元顺序形态变换的灰度图像边缘检测［J］.中国图象图形学报，2006，11（1）:41-46.