数学思想在地球运动类试题教学中的应用举隅
2011-09-06浙江省金华第一中学321015王洋平
浙江省金华第一中学(321015) 王洋平

自从公元前二世纪古希腊地理学家兼天文学家埃拉托色尼用几何学的方法计算地球的周长,奠定了数理地理的初步基础开始,就昭示着地理与数学的不解之缘。数学作为基本的问题解决工具,在中学地理教学中有着独特的作用,其结果的定量使得很多地理结论有了事实的依据和明确的数据。地球运动类试题一直是教学中的一大重难点,也是复习教学的重头戏。本文就结合地球运动类试题,谈谈一些基本数学思想在实际教学中的具体应用。
一、代数方程思想
例1(2010·浙江文综·6)读图1,某经线上有一点M,虚线为过M点地面垂直线,L1、L2分别是二至日正午太阳光线。当角α、β之差小于6°时,M点的纬度范围是
A.3°N~3°S
B.6°N~17.5°N
C.3°N~17.5°N或3°S~17.5°S
D.17.5°S~23.5°S或17.5°N~23.5°N
参考答案:A
1. 应用代数方程步骤如下
根据材料和图像可作图2(作M地平线m),可知∠1=90°-α、∠2=90°-β,因此α-β=∠2-∠1,另据材料可知∣∠1-∠2∣=∣αβ∣,即两者差值绝对值小于6°。设该地纬度为X,则有下列方程组:
X+23.5°=90°-∠1 ........ (1)
23.5°- X=90°-∠2 ........ (2)
(1)- (2)可得
2X=∣∠1-∠2∣=(0,6)……即0可取而6不可取,得知X=(0,3),即纬度范围为3°N~3°S。
2. 应用过程探析

图1

图2
分析和求解问题时,由描述的地理情景或题给条件,根据地理概念和地理规律,从时间关系、空间关系以及相关地理事物之间的数值关系等,建立方程(组),这是该类问题解决的基本策略。方程组的最终确立需要借助于地理原理,即用数学方程(组)的形式把地理原理进行定量表达,使地理结论更加明确和清晰,如方程(1)的确立就是建立于地理原理——两地纬度差即为两地正午太阳高度差。而最终结论的呈现,则只要把方程组简单的解出即可。这样使问题解决过程更加定量化,学生的模仿更加“有路可走”。
二、几何图形思想
例2(2010·金华模拟·9)图3弧S为某局部经线圈, M、N两地纬度相同,O为该经线圈圆心,某日太阳光与S位于同一平面且相切于M。此日M地的正午太阳高度为
A.0° B. α
C.90°—α D. 23.5°+α
参考答案:B
1. 应用几何图形步骤如下
依据所给可知,M、N两地纬度相同即两点中间有极点,而要寻求的就是α与该地正午太阳高度角之间的关联。根据同一纬度、同一经线圈的两点同时接受太阳,说明该地出现极昼,即分别为0点和12点时的太阳光线图。这是采用什么样几何图形的决策基础。
第一步:先用几何图像表示出两地的太阳高度,作M、N两地的地平线,相交于P(如图4)。
第二步:则有α+∠1+∠2+∠MPN=360°(四边形内角之和为360°)。

图3

图4
∠1+∠2=90°(两角皆为地平线和球半径的夹角),所以有α+∠MPN=180°。
第三步:∠3+∠MPN=180°(两角相邻为互补角),所以有α=∠3 。
第四步:∠3=∠4(两角为平行光线上的同位角),所以有α=∠4。
而根据太阳光与S位于同一平面且相切于M可知,M所在纬度是刚好出现极昼的纬度,而此时N即为正午12点,所以N地的太阳高度(图示∠4)即为M地的正午太阳高度。可知答案为B。
2. 应用过程探析
几何图形思想是指在对地理现象做出分析的基础上,通过反映题给条件或相关情景的几何图形(如题中四边形OMPN、太阳光线构成的一组平行线),应用地理规律(如题中地平线与球半径的夹角为直角、太阳光线是平行光等)和数学知识(如题中四边形内角和为360°、同位角相等等)求解地理问题的方法。地球运动中凡涉及空间的问题都多少与几何知识有关,诸如正午太阳高度、零时太阳高度、平行入射的太阳光线、纬度及纬度差、经线及经度差、自转和公转轨道图等都可以用几何图形表示,平时教学中也要多为学生用几何图形来表达相应的地理概念,为学生建立比较好的空间想象力,同时恰当的利用几何图像相关原理建立和佐证地理数据的不同相关性,这样为学生在解题和应用的迁移打下很好基础。
三、假设猜测思想
例3(2010·浙江模拟·9)图5中圆弧代表赤道,O为中心点,其中甲乙两点位于赤道,箭头代表地球自转方向。其中甲地两侧日期不同,乙地两侧昼夜情况不同。此时北京时间可能为
A.2:00 B. 8:00 C.18:00 D.22:00
参考答案:C
1. 假设猜测步骤如下
根据题中所给可知,甲是日界线与赤道交点,乙是晨昏线与赤道交点,但不管是晨昏线还是日界线均有两条,但也只是各有两条,所以假设猜测如下:
(1) 设乙为昏线与赤道交点,则乙地方时为18点。
(2) 设乙为晨线与赤道交点,则乙地方时为6点。
(3) 设甲为国际日期变更线与赤道交点,则甲位于180°附近。
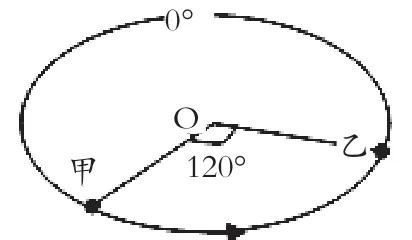
图5
(4) 设甲为昨天和今天交界线(即地方时为零点)与赤道交点,则甲地方时为0点。
上述的四种可能猜测中,根据甲在乙西侧120°可知甲地方时必小于乙8小时,所以如果甲地地方时为0点,则乙地方时为8点,均不符合(1) (2)两种对乙的假设,所以甲只能是符合(3)类假设,可知甲位于180°,而乙可以是上述的(1) (2)假设,可知甲(180°)地方时为10点或22点,所以北京时间即东八区为6点或者18点。
2. 应用过程探析
在试题给出的信息不是完全充分的情况下,特别是在结论有多种可能性时,虚设猜测思想是非常好的策略。假设猜测思想在数学中非常常见,即具体就是按给出的情景假设多种可能,最终在数学原则或者地理原理下进行对假设猜测的否定。一般否定原则来自于常见的地理概念、原理和现象,或者是题中所给条件(如上题甲乙夹角为120°)。应该说地理中广泛的用到假设猜测,如魏格纳的大陆漂移学说等。同时假设猜测可以拓展学生思维,同时也是一种很好的解决问题策略。平时教学中也要给学生充分的展示空间和假想猜测时间,不要急着给学生明白直接的答案。
四、辅助图像思想
例4(2010·全国卷Ⅰ·9)假设从空中R点看到地表的纬线m和晨昏线n,如图6所示。R点在地表的垂直投影为S,则S地的纬度

图6
A. 与M地相同 B. 介于M、N两地之间
C. 高于N地 D. 低于M地
参考答案:D
1. 辅助作图步骤如下
第一步:根据图像,画出一个符合题给图像的纬线m和晨昏线n分布图(如图7)。
第二步:寻找空中俯视点R。根据看到的纬线为直线,可知空中俯视点R应是纬线m的延长线上(即图7中的R点,当然也可在左边)。
第三步:寻找R点在地表的垂直投影S。垂直投影即为R点与地心的连线与地表的交点(图7中的S点)。
作图完成后,即可发现S点的纬度是低于M地。这样通过简单添加辅助线和复原完整图像的过程,解决问题与无形中。

图7
2. 应用过程探析
近几年高考中,局部图像是该类试题出现的基本载体,因此,在实际解题中,能更好的得到成像视角,恢复成完整图像是作辅助图的基本步骤,也是最主要的一步。该类图像的一般成像视角是侧视和俯视两种,所以高考类图像十之八九不会离开这两类母图。作辅助图像时,还需要根据试题实际,根据地理原理,作出符合要求的辅助线或者添加阴影,从而通过作图来探讨图中各要素之间的相互关系,或者直接得出结论。
综上所述的四类数学思想应为几乎所有的高中学生所具备的,这为其具体应用作了很好的铺垫。同时地球运动类试题,因其难度而困倒不少高三文科学生,特别是针对文科类学生普遍缺乏数学知识和空间想象能力,导致在实际解题和理解该类现象时,遇到不少障碍。因此,在地球运动知识的教学中,特别是高三的复习教学中,需要针对该类知识进行有效的数学思想渗透,多运用数学语言和数学方法表述地球运动知识和图像,以便更好的让数学思想、方法为地理服务。
