基于基尼系数法的县域经济差异分析——以陕西丹凤县为例

孙立硕

(西北大学城市与环境学院，陕西 西安 710127)

基于基尼系数法的县域经济差异分析
——以陕西丹凤县为例

孙立硕

(西北大学城市与环境学院，陕西 西安 710127)

以陕西丹凤县2009年各乡镇人口状况和人均收入为基础，运用基尼系数法探讨了丹凤县县域经济发展的分布规律。并根据所测算的基尼系数值对县域经济分布进行分析，结合乡镇产值排序序列给出发展建议。

基尼系数;县域经济;陕西丹凤

地区间经济发展的平衡性问题一直是国家、地方政府、社会和广大学者关注的热点问题。统计分析一定区域经济发展的时空演变规律，可以分析和判断该区域经济发展的平衡状况和居民收入分配差距，对于制定地区经济发展战略，确定经济发展的策略，促进地区之间的平衡协调发展，具有重要的理论和实践意义。县域范围内城镇发育序列完整，在区域内经济分配一定程度上能够自洽。本文试图运用基尼系数法对陕西丹凤县县域内经济发展的差异性进行分析。

基尼系数(Gini coefficient)是意大利著名经济学家基尼(C.Gini)于上世纪初期率先提出来的，现已成为世界范围内研究地区之间经济发展平衡状况和居民收入分配差距时被广泛采用的指标。尽管不少国内外学者在经济发展和居民收入的地区分配差距研究领域进行不断的努力与尝试，并且提出很多其他测量经济发展和居民收入的地区差距指标，比如变异系数、泰尔指数、锡尔系数等，但无论是这些指标的创新程度，还是其应用范围，均远不如基尼系数。基尼系数给出了反映经济发展状况和居民之间贫富差异程度的数量界线，能较为客观、明了地反映和监测不同地区经济发展状况和居民之间的贫富差距，预报、预警和防止居民之间出现贫富两极分化。这一方法得到世界各国的广泛认同和采用，具有普遍可信度。目前国内对基尼系数方法及其应用研究的成果较多。张进峰等对基尼系数的计算方法进行了探讨，李长林等对基尼系数和泰尔指数进行了比较，邓小红、葛霖生、陈南岳等探讨了基尼系数在我国的适用性，钱泽敏、龚红娥等对基尼系数的应用进行了实证分析，邹赟、尚宇红分析了我国基尼系数扩大的原因，提出了相应的对策，郭平等对提高我国基尼系数测算结果的准确性与可信度进行了思考，谢非讨论了基尼系数与社会公平之间的关系。本文以陕西省丹凤县2009年人口和人均收入为基础，旨在运用基尼系数对四川省经济发展平衡和地区收入分配差异状况进行实证分析。

1 基础数据资料的收集与整理

1.1 基础数据资料的收集原则

第一，完整性原则，即所搜集的数据资料必须准确、系统和完整，以保证统计分析的可靠性。第二，可比性原则，即统计分析的各种经济变量所发生的时间间隔应保持一致，以反映其在相同时间内所发生的经济现象的数量对比关系。第三，一致性原则，即所收集的观察期数据资料要保证其计算原理、计算方法和计量单位的一致性，总体范围的前后一致。

1.2 基础数据资料的收集与整理

笔者通过调查2009年以来丹凤县各地区人口和国内生产总值的统计资料。另从现有资料分析可知，所收集资料截止2009年，基本能反映丹凤县人口和社会经济发展的状况(人口单位采用人，人均收入单位采用元)，符合研究要求。现将其基本数据整理如下(表1)

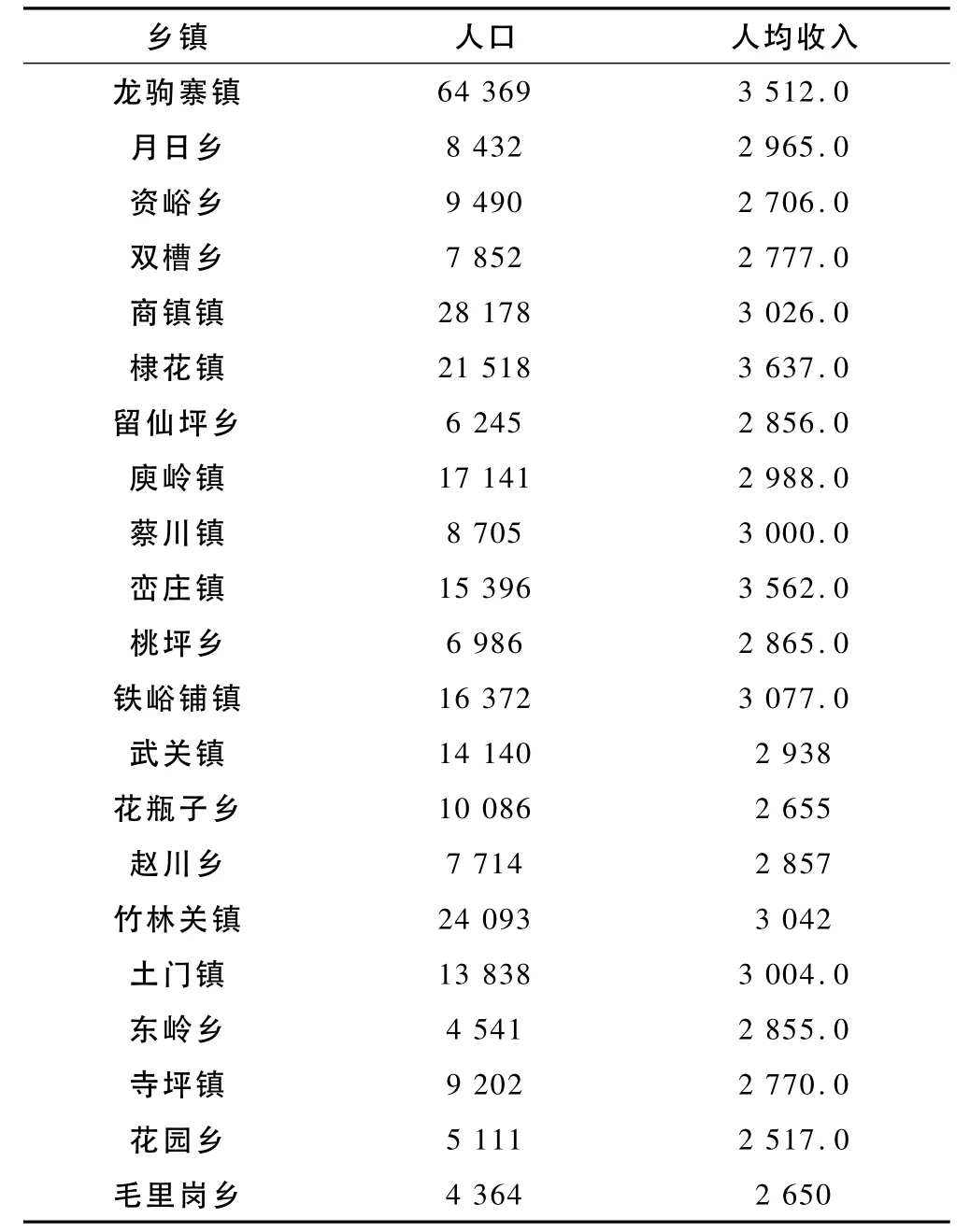
表1 2009年丹凤各镇人口和人均收入值

2 基尼系数法的基本原理

所谓基尼系数(Gini coefficient)，是通过两组数据的对比分析，纵横坐标均以累计百分比表示，从而作出洛伦兹曲线，然后再计算得出的集中化指数。它可通过对人口和GDP两组数据进行比较分析，然后将纵横坐标均以累计百分比表示，作出洛伦兹曲线，再计算集中化指数而得到的一个判断地区经济发展平衡程度的指标。其基本原理如下:

第一，列出每一地区的人口与GDP占全省的比重p和w;

第二，计算每一个区域的比率w/p;

第三，根据w/p值，由小到大将每一地区进行排序;

第四，按照上述顺序分别计算p和w的累计值X和Y;

第五，以H为横坐标，以 M为总坐标，在直角坐标系中依次连接各点，得到一条下条洛伦兹曲线(如图1所示);

图1 收入分配的洛伦兹曲线

第六，计算基尼系数。

假如洛伦兹曲线的解析表达式为:

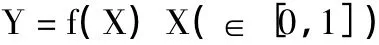
基尼系数(G)可按如下公式加以计算得到:

在实际运用中，因求解洛伦兹曲线解析式存在困难，常采取各种近似方法计算基尼系数.本研究根据分组数据，按照如下方法近似地计算:按人均收入由低到高进行排序，分成若干组，每组人均收入占总收入比重 Wi，每一组人口比重为pi，则基尼系数可以按如下公式近似计算:

3 经济发展的基尼系数分析

根据2009年丹凤县各乡镇的人口数和按照可比价格折算的人均收入数据，得出丹凤县县域基尼系数为0.36。

国际上通常用基尼系数来判定收入分配均等程度。基尼系数是界于0～1之间的数值，当基尼系数为0时，表示绝对平等;基尼系数越大，不均等程度越高;当基尼系数为1时，表示绝对不平等。市场经济国家衡量收入差距的一般标准为:基尼系数在0.2以下表示绝对平均;0.2～0.3之间表示比较平均;0.3～0.4之间表示较为合理;0.4～0.5之间表示差距较大;0.5以上说明收入差距悬殊。根据得出的基尼系数分析，可以得出如下结论:

第一，本文利用基尼系数法，计算了丹凤县的地区收入差距。计算结果显示丹凤县基尼系数在0.3左右，这表明丹凤县各乡镇经济发展水平差距不显著，收入分配总体比较均衡。

第二，丹凤县县域范围内各乡镇收入差距不是很大，呈现有序递减的序列，如2009年丹凤县农林牧渔服务业产值等值线图所示，镇域范围内产值等值线在县城驻地龙驹寨镇形成峰值，花瓶子乡形成次峰值;花园乡等值线处于谷底位置。县域内产值线走势较缓，表明产值分布较为有序。但收入的差距仍存在，峰值和谷底两者差距较大，且收入差距扩大的可能性仍然存在，这一情况应予足够的重视和关注。要从根本上解决地区收入差距问题，政府部门应有所作为，加大对落后地区的投资和政策扶持力度，引导资金和产业向落后地区流动。加快落后地区的城市基础和交通设施建设，充分发挥其资源优势，营造良好的投资环境。培养更多熟练的社会劳动力，加快落后地区的劳务输出。

图2 2009年丹凤县农林牧渔服务业产值等值线

第三，陕西省城乡人居收入基尼系数在2002年突破0.45大关，之后2005年至今更是稳定在0.45以上，接近警戒线。说明随着贫富之间的差异逐渐变大，收入分配的差异水平已经超出可承受范围。在全省乃至全国基尼系数呈逐步上升的背景之下，丹凤各乡镇的经济发展水平差距也呈现出逐年扩大趋势。其原因是县域内乡镇经济发展情况较为平均，乡镇产值明显分为三个梯队，龙驹寨和花瓶子乡处于第一梯队，11个处于第二梯队，8个处于第三梯队。且梯队间产值水平相差不大，递减曲线平缓。但是也应该注意到，一些经济基础较好的乡镇如龙驹寨，竹林关镇等，利用西部大开发的历史机遇以及自身有利的交通区位条件等，形成物流人流和信息流的中心，率先得到较快的发展，从而拉大了地区之间的经济发展差距，导致基尼系数逐渐增大。为了应对这种情况，使乡镇经济发展水平差距逐步缩小，应当大力发展基础相对薄弱的花园乡，赵川等部分地区，不断调整发展战略，充分发挥本地区的优势，主动向外招商，资金流入量增长快速，从而使经济得到了较快的发展，使地区之间的经济发展差距逐步缩小。

［1］张进峰，俞培果.按人群分组计算全国基尼系数:一种矩阵分解方法［J］.统计与决策，2006(23):142－143.

［2］高振碧.从基尼系数看我国收入分配问题［J］.甘肃农业，2001(12):22－24.

［3］黄继东.从基尼系数看我国居民收入的差距［J］.西南民族大学学报(人文社科版)，2003(10):64－67.

［4］唐莉，姚树洁，王建军.基尼系数分解分析中国城市居民收入不平等［J］.数量经济技术经济研究，2006(11):31－36.

［5］张洛民，王轶众.陕西基尼系数的实证研究［J］.管理观察，2009(12):237－239.

［6］陈昌兵.各地区居民收入基尼系数计算及其非参数计量模型分析［J］.数量经济技术经济研究，2007，24(1):133－142.

X2

B

1004－1184(2011)06－0179－02

2011－06－21

孙立硕(1986－)，男，河北石家庄人，在读硕士研究生，主攻方向:城市规划研究。