地震作用下不定位块体动安全系数计算与评价方法的探讨

徐栋栋

（长江科学院水利部岩土力学与工程重点实验室，武汉 430010）

地震作用下不定位块体动安全系数计算与评价方法的探讨

徐栋栋

（长江科学院水利部岩土力学与工程重点实验室，武汉 430010）

用块体理论分析方法中的矢量分析方法计算块体动安全系数，具体的研究思路是：首先输入构成不定位块体所需的结构面和临空面信息，然后根据有限性定理和可动性定理判断块体的有限性和可动性，在块体可动的基础上，再找出块体在自重和地震荷载共同作用下的滑动模式（脱离、单面滑动或双面滑动），并求出块体在该滑动模式下的安全系数，通过循环所有的地震时刻，得到了动安全系数时程曲线。考虑到不同区间安全系数的权值，提出了一种新的动安全系数评价方法，对动安全系数的评价指标做了探索工作。

块体理论；不定位块体；动安全系数；地震荷载；FORTRAN

1 块体理论简介

块体理论是20世纪70年代由石根华提出［1，2］，后来与R.E.Goodman教授合作完善起来的。它是借助于拓扑学、集合论、几何学和矢量代数学，对岩体稳定性进行分析的一种新方法，且已经广泛应用于边坡稳定分析、地下洞室稳定分析和隧道开挖稳定分析中。块体理论的具体分析手段有2种：一是矢量运算法，它将空间平面和力系以矢量表示，通过矢量运算给出全部块体理论分析结果；二是全空间赤平投影方法，该法简便、直观，仅需圆规、直尺作图，或用微机绘图，无需进行复杂的计算。这2种方法各自独立，所得结果一致，且都有严谨的数学证明。

1.1 块体理论的基本假定

（1）结构面为平面，对于每个具体工程，各组结构面具有确定的产状，并由现场地质测量获得。

（2）结构面贯穿所研究的岩体，即不考虑岩石块体本身的强度破坏。

（3）结构体为刚体，不计块体的自身变形和结构面的压缩变形。

（4）岩体的失稳是岩体在各种荷载作用下沿着结构面产生剪切滑移。

1.2 块体理论的2个定理［3］

1.2.1 有限性定理

设某凸块体由n个半空间的交集构成，平移各半空间界面使之通过坐标原点而形成棱锥。若棱锥为空集，则相应的凸块体为有限；反之，若棱锥为非空集，则相应的凸块体为无限。

块体为有限的充分必要条件是，裂隙锥与开挖锥的交集为空集。即

式中：JP为裂隙锥；EP为开挖锥；SP为空间锥；Φ为空集。

1.2.2 可动性定理

若由结构面和临空面共同构成的块体为有限，而仅由结构面构成的裂隙块体为无限，则该块体可动；若由结构面和临空面共同构成的块体为有限，而仅由结构面构成的裂隙块体亦为有限，则该块体为不可动，即为倒楔块体。

也可以这样来表述可动性定理，即块体可动的充分必要条件是

2 动安全系数计算及评价方法

文中关于不定位块体动安全系数的分析方法类似于动力有限元时程分析法［4－6］，即：该方法将每一时刻的地震荷载分别叠加到原块体自重上，形成新的主动力合力，在此基础上按照文中所述静力方法计算得到每一时刻块体的安全系数，最后得到其动安全系数时程曲线。此方法能够较好地考虑地震动力特性，直接给出每一时刻的地震响应，反映了地震过程中块体安全系数随时间的动态变化过程，能够了解块体在地震动力作用过程中稳定性程度的变化范围，但是如何选取一个合适的评价指标来表征整个地震动力作用过程中块体的稳定性是一个难题。刘汉龙等［6］提出用最小平均安全系数作为评价指标；张建海［7］、张伯艳［8］等提出用动力安全系数时程中的最小安全系数作为稳定性评价指标；赵剑明［9］等提出用动力等效值法评价边坡稳定性；刘红帅［10］等基于显式波动有限元方法，给出了动安全系数时程的计算方法，并引入可靠度的概念，提出了新的动力稳定性评价指标——可靠度动力安全系数，并给出了相应的计算方法。综合分析上述方法，最小动安全系数过于保守，平均安全系数可能会夸大块体的稳定性，动力等值法和最小平均安全系数缺乏明显的物理意义。而刘红帅等［10］也只是做了一个有益的探索，虽然将动力稳定性评价指标与工程风险紧密地结合了起来，却又多出一个动安全系数可接受的判断失效概率，有些顾此失彼。本文考虑了不同区间的安全系数权值，对动安全系数评价指标做了一些探索工作。

3 研究思路

本文采用块体理论分析方法中的矢量分析方法，便于编制程序。具体的研究思路是首先输入所需的结构面和临空面信息，然后根据有限性定理和可动性定理判断块体的有限性和可动性，如果该块体可动，再找出块体在自重和地震荷载共同作用下的滑动模式（脱离、单面滑动或双面滑动），并求出块体在该滑动模式下的安全系数，通过对所有地震时刻循环即可得到动安全系数时程曲线。同时根据文中提出的评价指标计算了动安全系数。文中仅讨论不定位块体，而对不定位块体只需考虑结构面的摩擦角。整个过程已经通过Fortran编程实现。

4 矢量分析方法的主要计算［3］

矢量分析方法的主要计算概括为判断块体的有限性计算、判断块体的可动性计算、滑动模式计算以及安全系数的计算，下面给出了各自的计算过程。

4.1 判断块体有限性和可动性基本步骤

（1）根据结构面产状，求出各结构面向上的单位法线矢量。

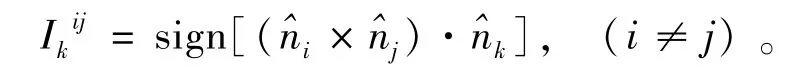
（4）将某块体的符号编号Dε＝［I（a1），I（a2），…，I（an）］编成“块体符号编号矩阵”［D］n×n，该矩阵中D（1，1）＝I（a1），D（2，2）＝I（a2），…，D（n，n）＝I（an），其余各项为0。

（5）建立该块体的“判别矩阵”［T］：

当［T］相应Iij的某行元素皆为“0”或同时含“＋1”和“－1”时，Iij不是该BP的棱；皆为“0”和“＋1”时，Iij为其真实棱；皆为“0”和“－1”时，－Iij为其真实棱。

根据上述步骤，首先根据已知的结构面信息判断块体是否有限，在块体有限的前提下加入临空面再判别是否可动。

4.2 判别块体滑动模式基本步骤

4.2.1 块体脱离岩体运动

要求＾vl＝sign（＾r·＾nl）＾nl（l为块体各结构面）。式中：＾vl为各结构面向内单位法线矢量；＾r为主动力合力方向。

要求＝－sign且＝sign（（l为块体各结构面，l≠i）。

4.2.3 块体沿双面i和j滑动

这样就可以找出相应各运动形式的JP编号。

4.3 块体安全系数的计算

（1）块体脱离岩体运动时，安全系数k＝0。

（2）块体沿单面滑动时，安全系数

式中Φi为该结构面的摩擦角。

（3）块体沿双面滑动时，安全系数

5 动安全系数评价方法

地震荷载下安全系数随时间的变化曲线，明确地表达了在特定滑动模式下块体的稳定性程度，为块体的动力稳定性分析奠定了基础。本文提出了一种动安全系数的评价方法，即：首先找出所有安全系数中的最大值，对其取整加1，然后分别统计在区间［0，1］，［1，2］，…，［N－1，N］内的各安全系数数目之和，求出各个区间安全系数数目占所有安全系数数目总和的比例，将其乘以各区间安全系数的平均值，将得到的值相加，即为动安全系数。公式如下：

式中：max（F）为所有安全系数中的最大值；sum1，sum2，…，sum N分别为区间［0，1］，［1，2］，…，［N－1，N］内安全系数数目之和；k1，k2，kN各区间安全系数数目所占的比例；sum K1，sum K2，…，sum KN分别为各区间安全系数之和；avr1，avr2，…，avr N分别为各区间安全系数平均值；K为动安全系数。

6 实例计算

6.1 结构面和临空面信息

构成块体的结构面和临空面信息如表1所示。

6.2 地震加速度时程曲线

如图1给出了某地区x方向的地震加速度时程曲线，可认为y方向与之相同，z方向乘以0.5，y与z方向的加速度时程曲线不再给出。

表1 结构面和临空面信息Table1 Information of the structural p lanes and free face

图1 地震加速度时程曲线Fig.1 Tim e history curve of earthquake acceleration

6.3 块体动安全系数时程曲线

经过程序判断可知编号为1101的块体可动，进而求得其动安全系数时程曲线如图2所示。根据本文中提出的动安全系数评价方法得出K＝1.402 31。而在只有自重作用时安全系数为1.326 207，说明地震作用有时利于块体稳定，而有时也会破坏块体稳定。

图2 BP1101动安全系数时程曲线Fig.2 Time history curve of the dynam ic safety factor of BP1101

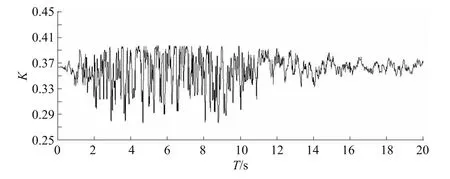
图3 BP1110动安全系数时程曲线Fig.3 Time history curve of the dynam ic safety factor of BP1110

经过程序判断可知块体1110可动，进而求得块体1110的动安全系数时程曲线如图3所示。根据文中提出的动安全系数评价方法得到K＝0.359 33，说明该块体处于不稳定状态，会发生滑动，需要施加支护措施。由图中亦不难看出安全系数均小于0.41。

7 结 语

文中对不定位块体在地震荷载作用下的稳定性进行了分析，并求得了块体的动安全系数时程曲线，据此可以直观地了解整个地震过程中块体稳定性的变化，具有实际的工程意义。实质上，本文的研究已将块体理论拓展应用到动力稳定分析，克服了传统块体理论仅是静力分析的不足。

若不考虑结构面黏聚力的影响，文中关于不定位块体动安全系数的计算方法可直接应用于实际工程中；当需要考虑结构面黏聚力的影响时，则必须将块体定位，以便于获得计算块体黏聚力时所需的块体的体积以及块体各面的面积等相关信息。前者计算得到的安全系数要小于后者。实际工程中，很多情况下都需要考虑结构面的黏聚力，因此需要对后者做进一步的研究。

文中关于动安全系数的评价方法具有一定的可行性，但是利用单一指标来评价块体的动力稳定性或许有些不足，能否考虑采用两个，或者更多的指标一起来评价块体的稳定性是一个很好的研究方向。

［1］ 石根华.岩体稳定分析的赤平投影方法［J］.中国科学，1977，（3）：269－271.（SHIGen hua.Stereographic Projection Method of Rock Mass Stability Analysis［J］.Science in China，1977，（3）：269－271.（in Chinese））

［2］ 石根华.岩体稳定分析的几何方法［J］.中国科学，1981，（4）：487－495.（SHIGen hua.Geometric Method of Rock Mass Stability Analysis［J］.Science in China，1981，（4）：487－495.（in Chinese））

［3］ 刘锦华，吕祖珩.块体理论在工程岩体稳定分析中的应用［M］.北京：水利电力出版社，1988.（LIU Jin hua，LV Zu heng.Block Theory and Its Application to Stability Analysis of Rock Engineering［M］.Beijing： Water Conservancy and Electric Power Press，1988.（in Chinese））

［4］ 刘红帅，薄景山，刘德东.岩土边坡地震稳定性分析研究评述［J］.地震工程与工程振动，2005，25（1）：164－171.（LIU Hong shuai，BO Jing shan，LIU De dong.Review on Study of Seismic Stability Analysis of Rock Soil Slopes［J］.Earthquake Engineering and Engineering Vibration，2005，25（1）：164－171.（in Chinese））

［5］ NEWMARK N M.Effects of Earthquakes on Dams and Embankments［J］.Geotechnique，1965，15（2）：139－160.

［6］ 刘汉龙，费 康，高玉峰.边坡地震稳定性时程分析方法［J］.岩土力学，2003，24（4）：553－560.（LIU Han long，FEI Kang，GAO Yu feng.Time History Analysis Method of Slope Seismic Stability［J］.Rock and Soil Me chanics，2003，24（4）：553－560.（in Chinese））

［7］ 张建海，范景伟，何江达.用刚体弹簧元法求解边坡、坝基动力安全系数［J］.岩石力学与工程学报，1999，18（4）：387－391.（ZHANG Jian hai，FAN Jing wei，HE Jiang da.Dynamic Safety Evaluation of Slopes or Dam Foundation Using Rigid Body Spring Element Meth od［J］.Chinese Journal of Rock Mechanics and Engi neering，1999，18（4）：387－391.（in Chinese））

［8］ 张伯艳，陈厚群，杜修力.拱坝坝基抗震稳定分析［J］.水利学报，2000，31（11）：55－59.（ZHANG Bo yan，CHEN Hou qun，DU Xiu li.Arch Dam Abutment Aseis matic Stability Analysis［J］.Journal of Hydraulic Engi neering，2000，31（11）：55－59.（in Chinese））

［9］ 赵剑明，陈 宁，常亚屏.地震作用下土石坝边坡抗滑稳定性分析［C］∥环境岩土工程理论与实践.上海：同济大学出版社，2002：239－248.（ZHAO Jian ming，CHEN Ning，CHANG Ya ping.Stability Analysis of Dam Slope Under Earthquake［C］∥Theory and Practice on Environmental Geotechnics.Shanghai：Tongji University Press，2002：239－248.（in Chinese））

［10］刘红帅，唐立强，薄景山，等.确定岩质边坡地震安全系数的新方法［J］.哈尔滨工程大学学报，2009，30（9）：1007－1011.（LIU Hong shuai，TANG Li qiang，BO Jing shan，et al.New Method for Determining the Seismic Safety Factor of a Rock Slope［J］.Journal of Harbin Engineering University，2009，30（9）：1007－1011.（in Chinese） ）

（编辑：曾小汉）

Com putation and Evaluation M ethod of Dynam ic Safety Factor for Unlocated Block under Earthquakes

XU Dong dong
（Key Laboratory of Geotechnical Mechanics and Engineering of the Ministry ofWater Resources，Yangtze River Scientific Research Institute，Wuhan 430010，China）

Considering theweight value of safety factors in different intervals，a new evaluationmethod for dynamic safety factor is proposed.Vector analysismethod of the block theory is adopted for programming.The detailed

research approach is presented as follows：first of all，the required information of structural planes and free face is input to form the unlocated block，and the finiteness andmobility of the block are determined subsequently accord ing to finiteness theorem and mobility theorem.If the block ismovable，find out the slidingmode（separating，sin gle face sliding or double face sliding）of the block under the combined action of dead weight and seismic load as well as the safety factor under that slidingmode.Finally the time history curve of dynamic safety factor is obtained by cycling all the earthquake times.This study can be regarded as an exploration in the evaluation index of dynamic safety factor.

block theory；unlocated block；dynamic safety factor；seismic load；FORTRAN

TU457

A

1001－5485（2011）08－0046－04

2010 08 13

徐栋栋（1986 ），男，山东聊城人，硕士，主要从事岩石力学与工程方面的研究工作，（电话）15994238327（电子信箱）xdhappy717＠163.com。