基于拉丁方阵的准循环LDPC码构造

陈集炜，赵泽茂，包建荣

(杭州电子科技大学通信工程学院，浙江杭州310018)

0 引言

低密度奇偶校验码(Low-Density Parity-Check，LDPC)［1］。证明其具有逼近香农限的好码［2］。自此，LDPC码开始成为信道编码的研究热点。近年来对LDPC码的构造方法研究逐渐转向准循环(Quasi-Cyclic，QC)LDPC码。QC-LDPC码是结构化LDPC码的一类。该类LDPC码性能优良、编译码复杂度较非结构化码低而受到研究者的关注。QC-LDPC码因其半结构化分块矩阵结构，便于硬件实现，同时具有优异的纠错性能，提出了一种LDPC码编码方法［3］。本文主要参考该LDPC码的基于拉丁方阵的三元系构造方法，提出了一种新的准循环LDPC码构造方法。方法是一种“Block-in-Block”的结构化构造方法，基矩阵采用拉丁方阵的Block构造思路，通过设定合适的移位系数，去除校验矩阵的6环。而且，它还可以构造任意码率、码长的QC-LDPC码，也更易于实现。

1 基矩阵的构造

1.1 基于拉丁方阵的构造方法

Milenkovic所提的编码算法利用斯坦纳三元系(Steiner Triple System，STS)，基于等幂、对称的拉丁方阵特性，并拥有结构化的构造［3］。Steiner三元系的定义:V是一个v元集合，B是V三元子集构成的集族。如果V中任意两个互异元素恰同时含在B的一个元中，则称(V，B)为v阶的Steiner三元系。拉丁方阵是一个m维方阵，其中每行每列都包含数集{1，2，…，m}。等幂的拉丁方阵是指拉丁方阵的(i，i)位置的元素为i，即方阵的主对角线上的元素为1，2，…，m的顺序排列;对称的拉丁方阵是指方阵的元素沿主对角线对称。

STS的构造方法具有严谨的数学结构:拉丁方阵的维数为2m+1;对应构造的LDPC码的校验节点数则为6m+3;对应的三元集数目为(3m+1)(2m+1)=(v(v－1))/6。校验矩阵的每列拥有2m+1个矩阵块，每行拥有m(2m+1)个矩阵块。由拉丁方阵得来的三元集被分成类型1与类型2两类［3］，第1类在LDPC码的校验矩阵中为维数为3的单位矩阵I，第2类则为右移位一位的维数为3的单位矩阵

1.2 构造方法性能分析

根据Steiner三元系定义，V中任意两个互异元素只同时含在B的一个元中。故文献3构造的校验矩阵不存在4环。文献3同时提出一种减小6环数目的方法:通过删除拥有最大6环数的列，来减少6环的数目。该方法具有一定的改进，但还存在不足。它仅是减小6环数，而不能完全去除6环。通过删除列来减少6环的方法，无法构造码率灵活与性能优异并重的LDPC码。本文在该构造方法引入QCLDPC码的特性，改进了该方法的不足。

2 构造QC-LDPC码

常见的QC-LDPC码又称为块状LDPC(Block-LDPC)码。块状LDPC码的校验矩阵H可表示如下所示。其中，I表示A×A的单位矩阵，又称循环置换矩阵;pi，j是其循环移位系数。若pi，j=－1，代表I(－1)是一个A×A的全零矩阵;若pi，j≥0，则代表单位矩阵I右移pi，j位。QC-LDPC码的校验矩阵H，可用简化的循环移位系数矩阵等价表示。矩阵P中的每个元素pi，j对应校验矩阵H中的每个循环置换矩阵的循环移位系数。

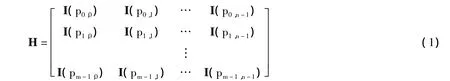
QC-LDPC码的校验矩阵H中所存在的长度为2l的块状环路，可用循环移位系数等价表示为:pi1，j1其中，pia，ja与 pia+1，ja+1在校验矩阵 H 的同一行或者同一列;pia，ja与 pia+2，ja+2不一定在同一行或同一列;a的取值范围为0≤a≤2l－2的任意值。

性质一［4］QC-LDPC码的校验矩阵H对应的Tanner图中存在一条长为2l的环路的充要条件是:环路上各基矩阵节点的循环移位系数满足:

而通过构造合适的移位系数矩阵，可以优化校验矩阵的环长，去除短环，使环长达到8环及以上。本算法构造的基矩阵不包含4环，所以仅需删去6环即可。

算法具体步骤如下:

(1)把生成的基矩阵Hb中的0元素置为－1，1元素置0，得到初始移位系数矩阵P0;

(2)初始移位系数矩阵P0的前3行的0元素保持不变，第4—6行的0元素，每行按正整数的顺序赋值，即分别赋值为1，2，3，…，p(1≤p≤A)，前6行的－1元素保持不变;

(3)从第7行开始，用式2检测0元素与以上几行的非零元素是否形成了小于8的短环。若没有则保持不变，否则生成一个取值范围为1≤p≤A的随机数p替换0元素;

(4)新生成的移位矩阵若满足式2，则产生另外一个不同的随机数进行替换，直至消去小于8环的短环。若在一定的次数内无法消去短环，则退回前3行，重新选择移位系数;在允许的一定次数内仍然无法消去短环，则退回前6行;并以此类推，直至得到矩阵P;

(5)将移位系数矩阵P的－1元素与非负元素分别用维数为A的全零矩阵OA与向右移位pi，j位的维数为A的单位矩阵替换，即得所需的校验矩阵H。

该移位系数构造法与传统的随机构造法不同处在于:因基矩阵是分块的矩阵，在选择移位系数的时，每块可选择相同的移位系数。

3 仿真及分析

3.1 性能仿真

根据上述编码构造原理，构造了不同码长的LDPC码，并与一些经典的随机构造LDPC码的误码性能进行了仿真比较。仿真参数如下:信道为二元输入高斯白噪声信道;译码算法采用置信传播(Belief-Propagation，BP)译码算法;最大迭代次数为50次;每个信噪比仿真误码达200个码字时，仿真结束。

仿真1 用本算法分别构造码长为480bit、990bit，码率都为1/2的LATIN QC-LDPC码，每个移位矩阵的大小分别为16×16与33×33，校验矩阵列重为3;同时构造对照的参数相同的PEG-LDPC码，进行局部围长仿真比较，得仿真结果如图1所示。

仿真2 用本算法分别构造码长为480bit、990bit，码率都为1/2的LATIN QC-LDPC码，每个移位矩阵的大小分别为16×16与33×33，校验矩阵列重为3;同时构造对照的参数相同的PEG-LDPC码，进行误码率仿真比较。仿真结果如图2所示。

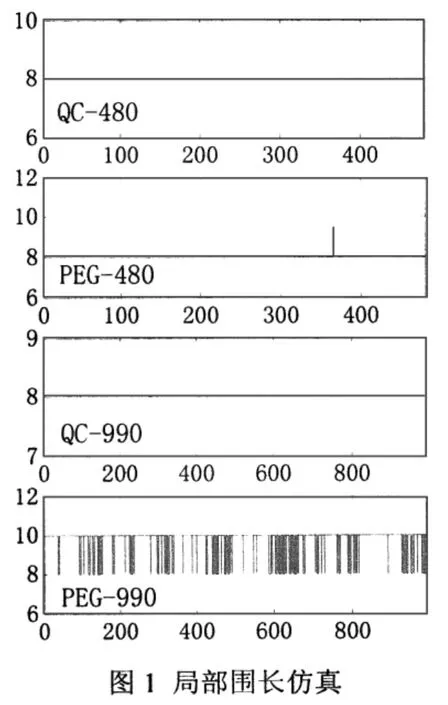
图1 局部围长仿真

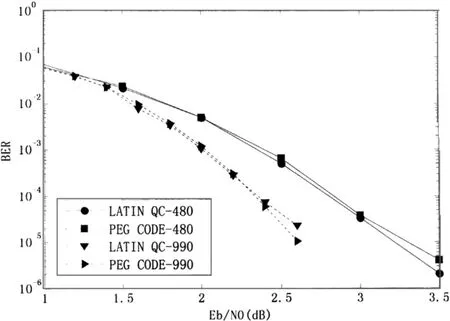
图2 误码率仿真对比图

3.2 仿真结果分析

PEG算法一直被认为是二元有限码长下次优的LDPC码构造方法［5］，故采用PEG算法与本算法对比具较强说服力。图1中的仿真结果表明，当码长为480bit时，LATIN QC-LDPC码平均围长与PEG算法构造的码字基本相等;而当码长为990bit时，LATIN QC-LDPC码因为其Block-in-Block的结构，平均围长不变，而PEG算法构造的码字的平均围长则大大大于Block-in-Block的结构。

图2中的仿真结果也表明了在码长为990bit时，PEG-LDPC码的误码性能稍优于LATIN QC-LDPC码:在误码率为10－5的数量级时，PEGPC-LDPC码比LATIN QC-LDPC码只有约0.1dB的增益;但在码长为480bit时，本算法构造的LATIN QC-LDPC码性能优于PEG-LDPC码。且在误码率为10－6数量级时，LATIN QC-LDPC码比PEGPC-LDPC码约有0.15dB的增益。PEG-LDPC码是随机构造的码字，而本文构造的LDPC码是“Block-in-Block”的结构，具有准循环特性，更易于硬件实现。

4 结束语

本文参考了拉丁方阵及Steiner三元系LDPC编码构造法，提出了一种QC-LDPC码的构造方法。仿真结果表明，本算法在构造的短码与PEG算法构造的码字相比，性能更好，且在误码率为10－6数量级时无明显的误码平底。同时，本算法所构造的QC-LDPC码，作为一种结构化构造的编码方法，非常有利于实际通信系统的硬件实现。

［1］ Gallager R G.Low density parity check codes［M］.Cambridge:MIT Press，1963:21 －28.

［2］ Mackay D J C，Neal R M.Near Shannon limit performance of low-density parity-check codes［J］.Electronics Letters，1996，32(18):1 645 －1 646.

［3］ Milenkovic O，Laendner S.Analysis of the cycle-structure of LDPC codes based on Latin squares［C］.Paris:Proc of IEEE International Conf on，2004:777 －781.

［4］ Myung S，Yang K，Kim J.Quasi-cyclic LDPC codes for fast encoding［J］.IEEE Trans on inf Theory，2005，51(8):2 894 －2 901.

［5］ Hu Xiao-Yu，Evangelos Eleftheriou，Dieter M Arnold.Regular and irregular progressive edge-growth tanner graphs［J］.IEEE Trans Comm，2005，51(1):386 －398.