大型水电站地下厂房的水力振动数值分析

2011-09-03张运良赵晓峰吴嵌嵌马艳晶

水力发电 2011年8期

关键词：转轮水头脉动

张运良，韩涛，侯攀，赵晓峰，吴嵌嵌，马艳晶

（1.大连理工大学建设工程学部水利工程学院，辽宁大连 116024；2.中国水电顾问集团成都勘测设计研究院，四川成都 610072）

1 地下厂房动力分析模型

随着水电机组容量和水头的不断提高，机组和厂房的水力振动问题日益得到重视。研究水力振源作用下的动力反应，对厂房振动加以预测和设计优化，以防止和控制剧烈振动的发生，确保结构安全，具有重要意义。

目前，动力反应分析针对地面厂房的较多[1-4]，而对地下厂房则相对较少。地下厂房的动力分析比地面厂房更复杂，涉及到围岩-厂房的动力相互作用以及对远域的无限围岩介质的有效模拟。

在当前水电站地下厂房动力分析中，在厂房-围岩交界面或在截取一定范围的围岩外边界处施加法向和切向集中弹簧，以模拟围岩对厂房的动力作用。这种处理是仿照静力分析的做法，认为围岩仅提供静态弹性支撑[3]。另外，法向弹簧刚度系数系由静态弹性抗力系数转化而来，而切向弹簧刚度的确定则无依据。对于动力分析，这样的做法显然在理论上欠妥。另外，这种处理没有考虑围岩介质的几何辐射阻尼对振动散射波的吸收作用，在截断边界处将产生虚假反射，且限于计算规模，围岩范围不可能取得足够大，将不可避免地造成计算结果失真。

若在截断围岩边界处除了施加集中弹簧以考虑围岩的弹性支承作用外，另再施加集中粘性阻尼器以模拟对散射波的吸收作用，则围岩和厂房的动力相互作用系统在内源如水力振源激励下的动力反应在相对较小的计算范围内就可近似正确求解。这种由粘性阻尼器和弹性弹簧等基本物理元件所构成的人工边界已在地震工程和岩土工程等领域中有了较多应用，而很少应用于水电站地下厂房的水力振动研究[7]。本文采用粘弹性边界理论，以溪洛渡水电站为例，进行了大型地下厂房的水力振动反应分析和评价。

首先，厂房与一定范围的围岩在进行有限元网格剖分后，在截断边界上某一节点i施加的集中弹簧和阻尼器参数[5]为

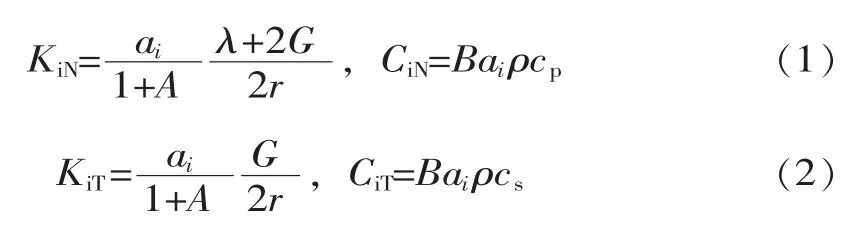
式中，KiN，KiT分别为边界i节点的法向和切向弹簧刚度；CiN，CiT分别为i节点的法向和切向阻尼系数；ρ为介质密度；G和λ为拉梅常数；cp和cs分别为P波和S波的波速，无实测值时可由弹性常数估算；ai为节点i的控制面积；长度r可取为主厂房洞室几何中心到人工边界点所在边界线或面的距离；参数A和B可分别取值为0.8和1.1。

采用粘弹性边界理论及相应的动力输入方法，笔者已成功进行了水电站地下厂房洞室群的地震反应分析[6,7]。

2 工程概况、计算模型和参数

金沙江溪洛渡水电站是目前国内在建的最大的水电工程之一，单机容量770 MW。发电厂房为地下式，埋深超过300 m。由于运行水头高，电站建成后可能会因防洪和负荷调节的要求而偏离设计工况运行，水头变幅较大，因此在设计阶段厂房的振动反应引起了重视。

主厂房采取一机一缝布置方式，标准机组段间距为34.0 m，厂房上下部跨度分别为31.9 m和28.4 m，高79.6 m，主变室断面尺寸为19.2 m×32.8 m（宽×高）。蜗壳采用垫层和直埋组合的结构形式。

计算模型取中间一个完整的机组段主厂房连同一定范围的围岩。围岩的具体模拟范围为：横流向取一个机组段长度34 m；自上游边墙向上游方向取85.2 m，自下游边墙向下游取103 m，分别约为机组段顺流向长度（28.4 m）的3倍和3.5倍。竖直方向以机组轴线为基准向上取170 m，向下取145 m，分别约为厂房高度46.5 m（从发电机层楼板高程376.50 m至尾水管底板高程330 m）的3.7倍和3.1倍，模型总高度为315 m。模型中考虑了从发电机层楼板高程至尾水管底板高程间所有的混凝土结构构件，其中包括主要的孔洞和廊道。因主变压器洞室距离主厂房洞室较近，模型中也作了反映。

机组段两侧考虑结构分缝，各层楼板由梁柱支撑，按自由边界处理；水轮机层以下大体积混凝土以及上下游支撑楼板的立柱因与围岩紧密接触，计算中按共用节点处理。围岩截断外边界施加粘弹性边界，其边界元件参数由式（1）和式（2）确定。

厂房-围岩整体的半剖面和部分有限元模型网格剖分见图1。计算采用的材料参数见表1。

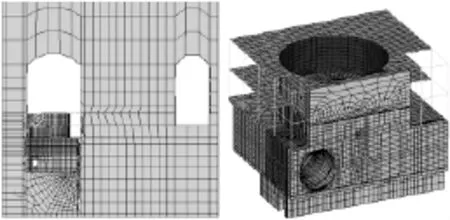
图1 主厂房-主变室-围岩部分及厂房结构有限元网格

3 脉动水压力试验概况

沿流道共布置了9组压力脉动测点，位置为蜗壳进口（点 1），尾水锥管距转轮出口 0.30D2上下游侧（点2、3），尾水锥管距转轮出口1.00D2上下游侧（点6、7），导叶后/转轮前上下游侧（点4、5），尾水肘管上下游侧（点8、9）。试验采样频率为2 000 Hz，采样时间16.3 s。工况选择从空载到满负荷，覆盖电站所有实际运行水头范围。

机组运行时产生的主要是与转频有关的脉动压力荷载，其主频率与转速成正比，幅值与水头成正比。同一工况下，原型和模型脉动压力的频率和幅值相似，转换关系为：

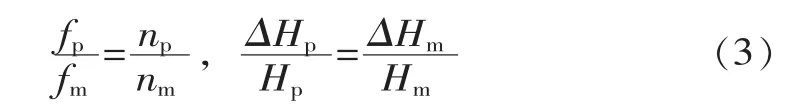
式中，fp，np分别为原型的频率和转速；fm，nm分别为模型的频率和转速；ΔHp和ΔHm分别为原型与模型的脉动压力水头；Hp和Hm分别为原型与模型的工作水头。

综合厂家提供的所有脉动压力试验资料并考虑厂房与机组振源的共振复核成果，本文选择以下典型计算工况：

（1）工况1。原型水头229.4 m （对应试验水头为30.29 m），机组出力950.27 MW。导叶后/转轮前的典型压力脉动时程曲线及其傅立叶（Fourier）谱见图2、3。如图2、3可知，导叶后/转轮前压力脉动ΔH/H最大值为3.35%，模型压力脉动主频为200.55 Hz （按式（3）换算到原型约为 31.14 Hz）。此工况定性为以不均匀水流撞击叶片引起的转轮振动为主。本工程水轮机转轮叶片数为15，水力激励主频31.14 Hz数值上等于机组转频（fn=2.08 Hz）的14.97倍，即接近所谓的叶片数频率。

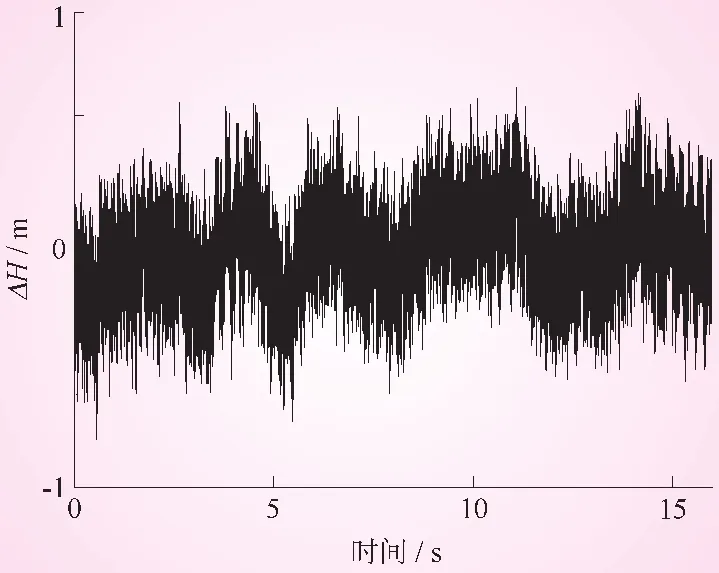
图2 工况1，导叶后/转轮前的典型压力脉动时程曲线(以试验脉动水头表示)

图3 工况1，导叶后/转轮前的典型压力脉动傅立叶频谱

（2）工况2。原型水头213.0 m （对应试验水头为30.00 m），机组出力128.90 MW。尾水管距转轮出口0.30D2处压力脉动最大值为5.19%，原型中激励主频约为4.20 Hz，为机组转频的2.02倍。此工况定性为以尾水管内中频涡带引起的振动为主。

（3）工况3。原型水头154.6 m （对应试验水头为31.09 m），机组出力249.08 MW。尾水管距转轮出口0.30D2处压力脉动最大值为4.23%，原型中激励主频约为0.52 Hz，为机组转频的1/4。此工况定性为以尾水管内低频涡带引起的振动为主。

4 计算结果与分析

4.1 振动幅值

分析采用纽马克（Newmark）时程积分法和瑞雷（Rayleigh）阻尼，阻尼比取为0.05。限于篇幅，计算结果仅给出了发电机层和电气夹层楼板、定子和下机架基础等几个主要部位各方向的振动位移、速度、加速度等正/负向幅值（见表2）。由表2可知，厂房的竖向振动反应幅值显著大于水平向；竖向振动位移、速度和加速度幅值基本上以工况2为最大，工况1次之，工况3最小。工况1和工况2相比，反应振幅差别不大，但均明显高于工况3；同一种工况下，随着高程的增加，竖向振动位移幅值逐渐减小，而竖向振动速度和加速度幅值却逐渐增大。

另外也整理了主要混凝土构件和钢部件的振动应力，因幅值与相应的强度值相比很小，本文不再给出。

4.2 频谱反应特性

以加速度反应为例进行简要说明。

在以不均匀水流撞击叶片引起的转轮振动为主的脉动水压力作用下（工况1），各部位的反应都具有共同的主频31.28 Hz，几乎就等于激励主频31.14 Hz，因此可认为此工况的振动反应主要是由不均匀水流撞击叶片所引起的。例如，图4、5分别为发电机层靠近下游侧与风罩相连处的结点竖向振动加速度时程曲线及其傅立叶频谱。

图4 工况1，发电机层楼板典型结点竖向振动加速度时程曲线

图5 工况1，发电机层楼板典型结点竖向振动加速度傅立叶频谱

在以尾水管内中、低频涡带为主的脉动水压力作用下（工况2和3），与工况1相比，各部位的振动反应频谱构成相对较为丰富，频带也较宽。例如，工况2下的发电机层楼板和电气夹层楼板部位的加速度反应主频约为28.14 Hz；对于定子基础和下机架基础部位，则约为23.65 Hz。

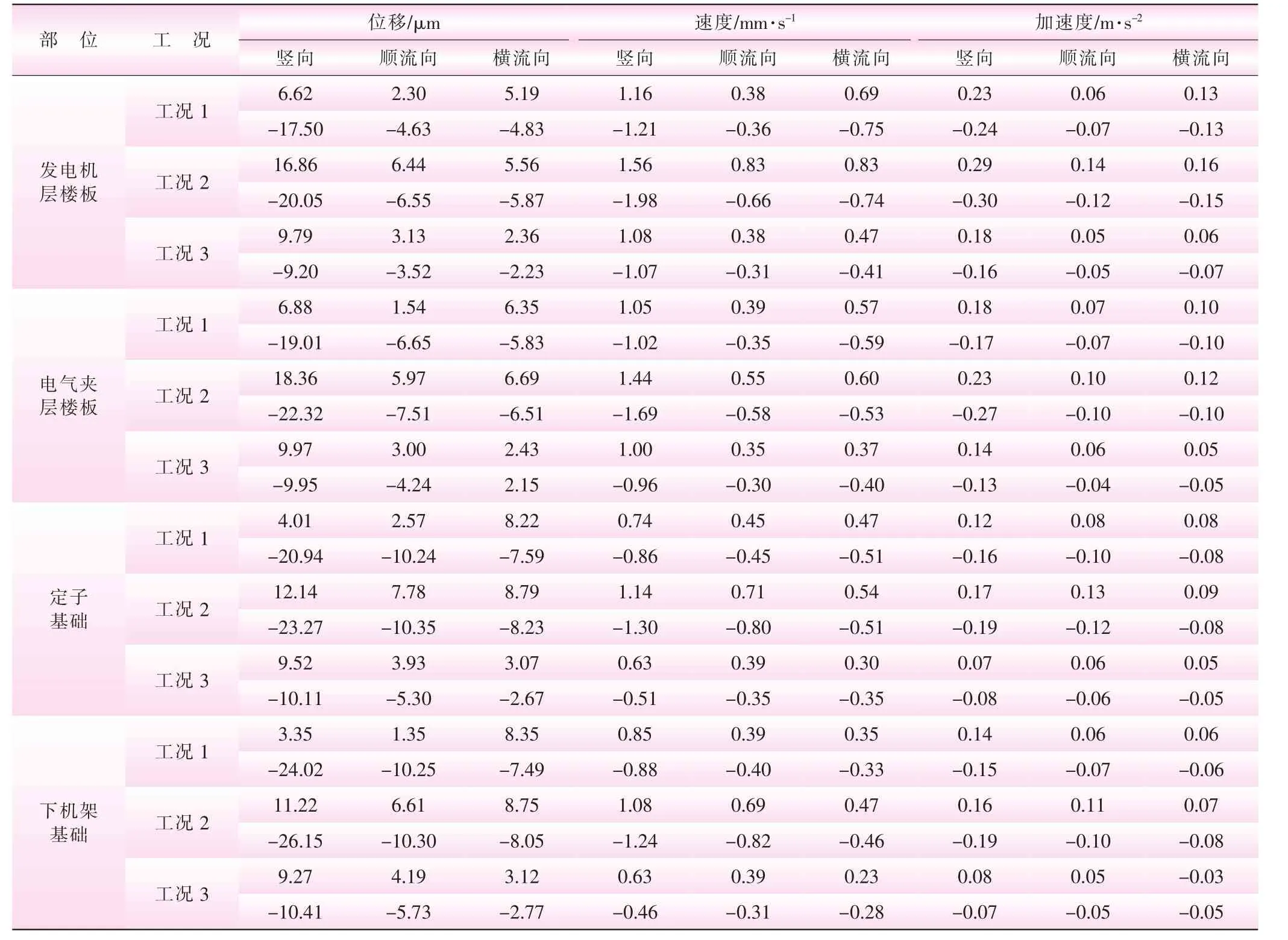
表2 厂房主要结构各方向振动反应正/负向最大值

5 水力振动评价

文献[4]经对国内外的相关建筑物、机械设备、仪器仪表和人体保健等方面的振动控制标准进行归纳和总结，提出了水电站厂房振动控制标准建议值（见表3）。结合本文的计算结果，参考该建议值进行振动评价。

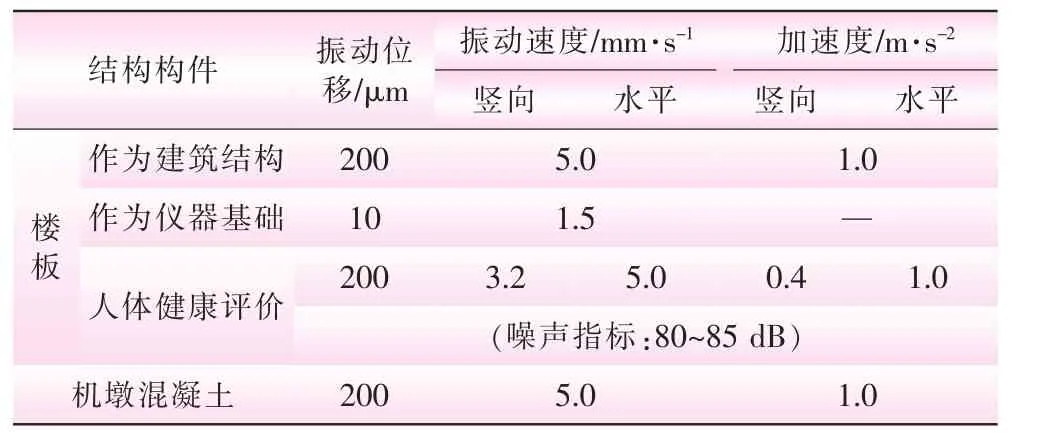
表3 水电站主厂房振动控制建议值[4]

因流道内脉动压力作用下各工况的激励主频率都不接近于结构自振频率，厂房各主要薄弱部位产生的振动反应均很小，位移、速度和加速度振动反应都小于建议的振动允许限值。另外，厂房各主要部位的振动应力数值也都很小，对结构的强度安全性不构成显著影响（这进一步说明本文采用线弹性模型进行动力分析是合适的）。综上，流道内脉动压力作用下主厂房的各主要部位能够满足抗振要求。