基于美国佛罗里达州Orange县的宏观交通安全建模分析

吴杏薇， 王雪松， 金 昱

（1.同济大学 交通运输工程学院，上海 201804；2.上海城市规划设计研究院，上海 200040）

目前中国正处于城市化和机动化水平飞速增长的关键时期，考虑到交通规划对城市交通系统塑造的关键作用和城市交通系统一经形成便难以改变的不可逆性，亟需倡导在交通规划阶段重视交通安全，利用先进的分析方法深入分析路网空间特征、区域交通特征与区域交通安全的机理，以指导构建一个安全的交通系统。

近年来，世界各国已经越来越重视在交通规划整个过程中充分考虑交通安全，并且已经做出大量定量研究［1－5］来分析道路区域属性特征、交通特征及区域其他影响因素与交通安全的关系，其中以交通分析小区（Traffic Analysis Zone，简称TAZ）层面的研究成果最为丰富。国外宏观交通安全研究主要从区域人口经济［2，5－7］和土地利用特征［8］、区域交通运行 特征［2，6，9－10］、区域道路属性特征［2，5－7］等几个方面进行分析。在已有研究中，对于区域道路网络特征变量的分析，仅仅是以区域为单位的设施数量的简单累计，这些特征的简单提取并不能充分反映道路网络空间结构特性，没有从路网功能、拓扑结构深度挖掘事故发生的根本原因，需要结合复杂网络、拓扑结构等学科的理论与方法来进一步研究区域路网空间结构对于宏观安全的影响。就统计方法而言，文献［6－7，11］利用广义线性模型（General Linear Model，简称GLM）技术来对TAZ事故数同解释变量的关系进行建模，误差项假定服从泊松或负二项分布。在GLM建模框架下，假设TAZ事故数量的分布是非空间相关的，而现实中宏观安全数据具有复杂的空间分布。交通分析小区在空间上有远近之分，相邻的小区在社会经济发展、道路交通特征上有某种程度的趋同性，距离较远的小区之间有某种程度的相异性。为了克服传统统计分析方法在分析空间数据上的缺陷，空间统计方法［12］逐步被用到宏观安全分析中。贝叶斯空间统计方法由于可以满足数据的空间相关性以及模型的复杂性，已经在宏观交通安全分析中发挥着越来越重要的作用。

国内已有的研究主要集中于对城市各类道路设施如城市交叉口安全性的分析［13－16］。文献［17］讨论了如何结合我国交通规划工作的工作流程考虑交通安全；文献［18］提出了“主动道路交通安全规划”这一概念。国内城市总体规划、土地利用规划中都很少考虑交通安全，现实中许多规划对规划区内的交通安全造成了直接或潜在影响，文献［19］对城市总体规划和土地规划中影响交通安全的因素进行了探讨。但是，纵观国内的研究，就所使用的安全分析方法而言，对事故安全分析模型的研究和应用还很少，统计分析也主要是应用多元线性回归和传统的广义线性回归［13－15］，而反映路网特征、交通特征与交通安全之间关系的定量研究在我国尚未展开。

由于美国基础数据较为完善，本研究依托美国佛罗里达州Orange县的数据，以TAZ作为分析单元，借鉴复杂网络、拓扑结构学科知识提取能够有效反映路网结构的特征指标，并利用先进的贝叶斯空间分析方法建立统计模型，分析区域路网特征、交通运行特征和区域其他影响因素与交通安全之间的关系。

1 数据准备

宏观安全模型的建立需要的数据包括区域人口经济和土地利用数据、区域道路网络信息、区域交通运行特征信息以及区域事故数据。本文选取美国佛罗里达州中部Orange县2006年的事故、道路、交通、人口、土地利用等较为理想的数据进行研究，数据来源主要有佛罗里达州交通厅（Florida Department of Transportation，简 称FDOT）、美国统计局TIGER数据、中佛罗里达区域规划模型。

1.1 人口与土地利用

人口数据均来自美国统计局2000年统计数据，并通过2006年全县人口分别对各个TAZ进行同比例扩算。在美国，人口统计的基本单元称为人口普查街区。通常情况下，一个TAZ由多个人口普查街区组成，通过GIS（Geographic Information System）空间关联工具，可以计算出各个TAZ的人口总数、人口组成以及家庭情况。对于土地利用情况，分别用0、1、2代表完全城市化、部分城市化和郊区，利用空间关联关系计算出各个TAZ的城市化程度和学校数量。

1.2 道路、交通特征

本文中使用的交通数据主要来自FDOT，主要是道路分段AADT数据和信号灯位置数据，通过AADT数据计算出TAZ内道路车公里数（Vehicle ilometers of Travel，简称VKT），通过信号灯位置计算各个TAZ内州道上信号灯数量和密度。

道路数据相关变量的计算分为2大类：道路、交叉口规模指标和路网结构指标。规模指标包括各类道路长度、密度以及各类交叉口的数量、密度。结构指标主要包括道路网内各种道路的类型，道路网络的等级级配以及道路网络中各条道路间相互衔接的关系。本文中主要通过提取路网形态特征指标meshedness值来实现。

群聚性（clustering）是网络分析中一类非常重要的指标，用来衡量网络中顶点的积聚程度。文献［20］提出meshedness值算法是一种简单且具有普适性的算法，它通过计算网络中三角形圈型结构数量同该网络中所有顶点对应的完备平面图中三角形圈型结构数量的比来反映网络的群聚性。如果网络中圈型结构多，则meshedness值高，顶点间联系紧密，积聚程度高；反之，如果网络中圈型结构少，则meshedness值低，顶点间联系松散，积聚程度低。

对于一个由K条边、N个顶点组成的网络G，meshedness值计算公式为：

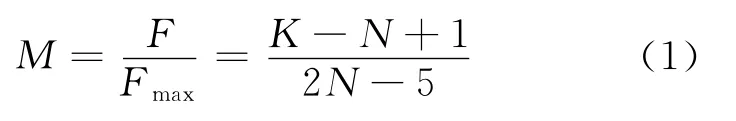
其中，F为由欧拉公式计算出的网络中面（face）的个数，Fmax为N个顶点组成的网络可能拥有最多的面的数量。

将现实的道路网络变换为抽象网络，如图1所示，基于路网图层（shapefile）和TAZ图层，利用计算机相关程序计算出各个TAZ对应的meshedness值。

图1 原始法解析道路网图示

基于文献［21］的研究，本文将道路网络形态分为方格网、平行曲线结构、尽断路＋环形路结构、离散型和混合型5种类型。其中离散型是指TAZ内道路网离散、分块分布；混合型路网是指TAZ道路网形态含有方格路网、平行曲线路网、尽端路＋环形路中2种及以上路网形态。相应地分析这5类路网的meshedness值分布情况，分析结果表明meshedness值对5类路网具有很好的区分度，具体结果见表1所列。

表1 路网分类与meshedness值离散化处理结果

2 事故数据

事故数据由FDOT提供，它们以点的形式存储。为了计算各个TAZ内的事故数量，首先需要分析每个事故点相对于TAZ边界的空间位置。如果事故点不在TAZ边界上，它的归属是明确的。对于TAZ边界上的事故，本文以TAZ边界的道路中心线为事故归属的分界线，从FDOT事故报告系统中提取每起事故中各车辆行驶方向（东、西、南、北）和事故原因信息；然后对于每起事故，编制计算机程序，确定事故点相对于TAZ边界的精确位置关系，从而确定事故精确归属。

综上所述，本文中所有变量描述性统计结果见表2所列。

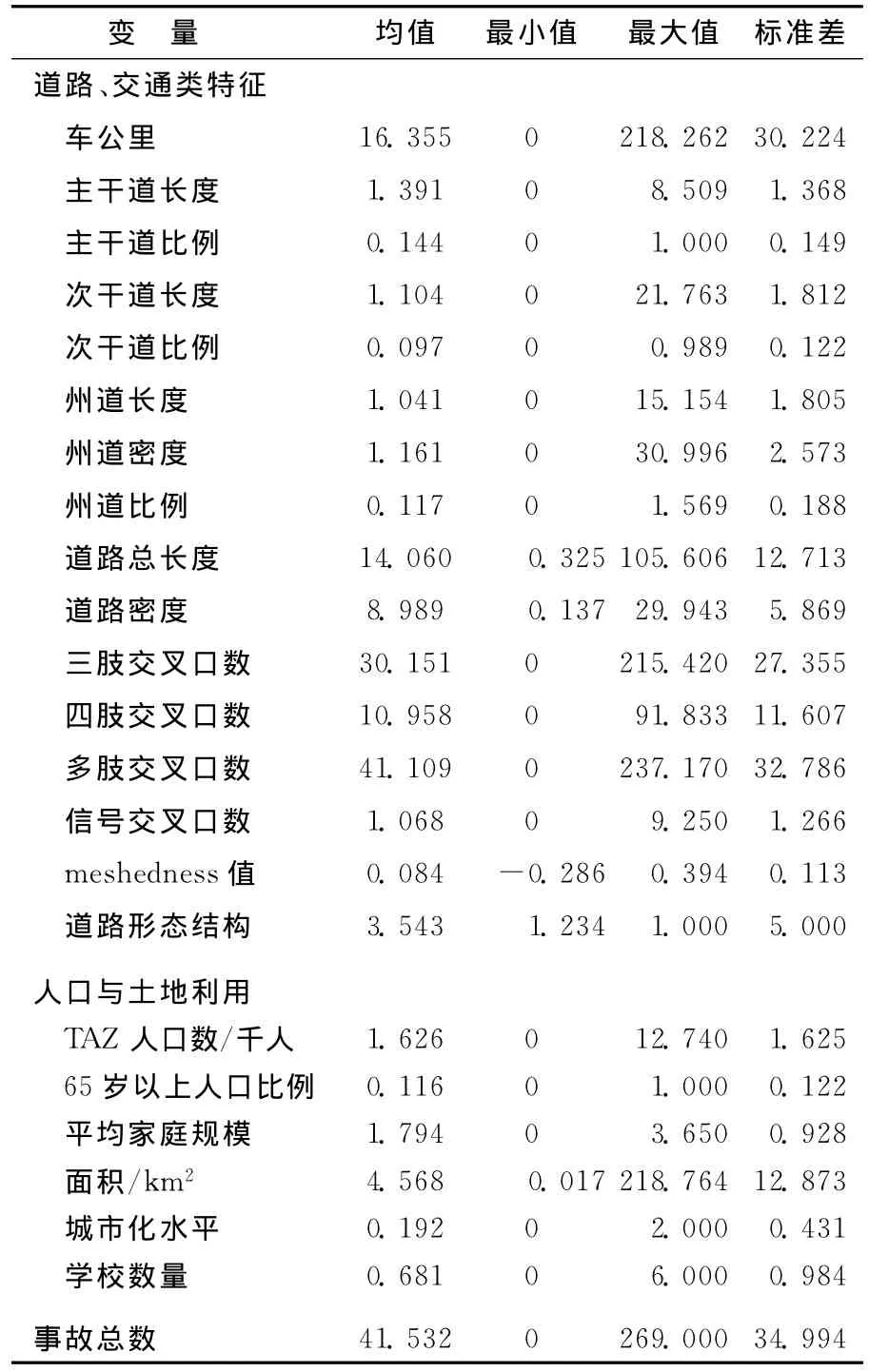
表2 Orange县变量的统计性描述

图2所示为Orange县离散化后的meshedness值分布情况。可以看出道路网络形态分布呈现一定的空间积聚性，市区多为方格网、平行曲线路网结构，郊区多为尽端路＋环形路和离散型路网结构。

图2 Orange县TAZ路网形态分布图

3 模型方法

3.1 贝叶斯分析方法

贝叶斯学派主张未知参数是一个随机变量，具有随机性，在统计推断的过程中，贝叶斯学派不仅利用总体信息和样本信息，还利用先验信息进行统计推断。贝叶斯定理［22］表述为：

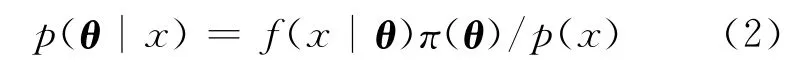
其中，θ 为参数向量；x＝（x1，x2，x3，…，xn）为样本；π（θ）为参数向量θ的先验分布；f（x｜θ）为似然函数；p（θ｜x）为给定样本x信息后参数向量θ后验分布（或称为后验），即抽样后人们对未知参数分布的重新认识；p（x）为x的边缘分布。

相比于传统频率学派的估计方法，贝叶斯分析不仅能灵活地调整模型以满足需要、方便地计算便于理解的统计推断结果［23］，而且对复杂数据结构有较好的拟合性［24］。

3.2 CAR空间模型

研究区域内的TAZ空间上并不是互相独立的，临近的TAZ常表现出类似的安全水平。为了解决空间相关问题，统计学家建立了一系列空间回归模型，条件自回归（Conditional Autoregressive Model，简称CAR）模型便是其中的代表。CAR模型在GLM假设基础上引入随机效应项φi，用以解释第i个TAZ同其他TAZ间的空间相关性，GLM中设定的事故模型［25］为：

通常利用空间邻接矩阵W来说明空间内任意2个TAZ的关系。本文中该矩阵定义如下：

从而，在贝叶斯CAR模型中，φi的先验条件分布可定义为：

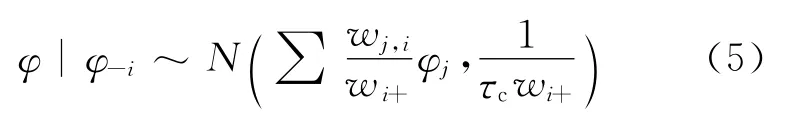
其中，φ－i为除φi外所有的φ的集合；τc为精度系数（precision parameter）；wi＋为同 TAZi相邻的TAZ的wi，j的和为同i号 TAZ相邻的TAZ的集合。

φi的联合先验分布为：

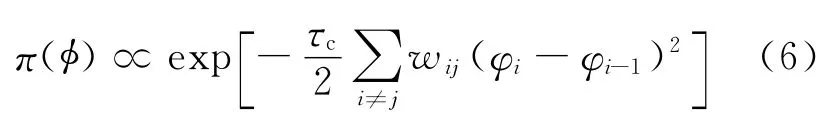
其中，π（φ）为φ（φ＝｛φi，i＝1，2，3…｝）的联合分布；∝说明左式的似然方程同右式同比例变化。进而可由先验分布计算后验分布，并完成统计推断。

针对贝叶斯CAR模型，使用由文献［26］提出的误差信息准则（Deviance Information Criterion，简称DIC准则）来比较模型的优劣。DIC准则从拟合优度和模型复杂性2个方面综合地考察模型，其计算原理［27］是“DIC＝‘模型拟合优度’＋‘模型复杂性’”。DIC值定义为：

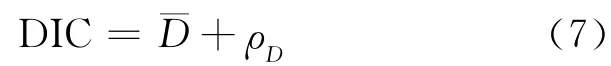
其中，ρD为有效参数数量，用来衡量模型复杂性。一般地，DIC越小，说明模型拟合效果越好。若新模型DIC值比旧模型DIC值低且差值多于5，则说明新模型较优［25］。

4 模型结果

4.1 模型比较

基于2006年美国Orange县数据，用TAZ内所有事故数量作为因变量，分别建立了贝叶斯泊松回归模型和贝叶斯泊松CAR模型。表3所列为模型间DIC值及¯D、ρD值的比较结果。贝叶斯泊松CAR模型DIC值远低于贝叶斯泊松模型，说明贝叶斯泊松CAR模型拟合效果大大优于贝叶斯泊松模型；其次，贝叶斯泊松CAR模型的ρD值大大高于贝叶斯泊松模型，说明贝叶斯泊松CAR模型的结构较贝叶斯泊松模型复杂。

表3 模型DIC值比较

4.2 模型标定结果与变量分析

表4所列为利用MCMC方法模拟计算出的参数后验估计结果，包括后验均值（posterior mean）、后验标准偏差（posterior standard deviation）和95%可信区间。

置信区间是通过结合模拟结果的2.5%分位数和97.5%分位数获得。如果置信区间内不包含0，则说明对应变量在95%显著性水平下是显著的；如果包含0，则对应变量不显著。

从模型中可看出，对TAZ事故总数有显著影响的因素包括人口总数、老年人口比例、交叉口数量、主干道长度比例、主干道上信控交叉口数、道路总长和路网形态等。

4.2.1 路网形态变量

模型标定结果显示，meshedness值不仅具备对路网进行分类的能力，同时也能较好地反映路网形态对安全的影响，随着meshedness值的升高，事故数量降低了。从模型结果可看出，以方格网路网和平行曲线路网作为基准，除了混合模式的路网对于事故发生的影响不显著以外，尽端路＋环形路路网对事故的影响是显著为负的，这可能同这类路网道路平行曲线半径较小、支路接入主要道路控制等因素有关。在其他条件相同的情况下，尽端路＋环形路路网事故数量仅为方格路网事故数量的exp（－0.225）＝86.4%。最为安全的是离散型路网，原因可能是道路连接点少、交通需求小、交通可能的冲突点和冲突量少。在其他条件相同的情况下，离散型路网事故数量仅为方格路网事故数量exp（－0.986）＝46.2%。但是，由于这类路网所在TAZ路网发育还不成熟、地广车少，所得结果对交通规划的指导性不强。

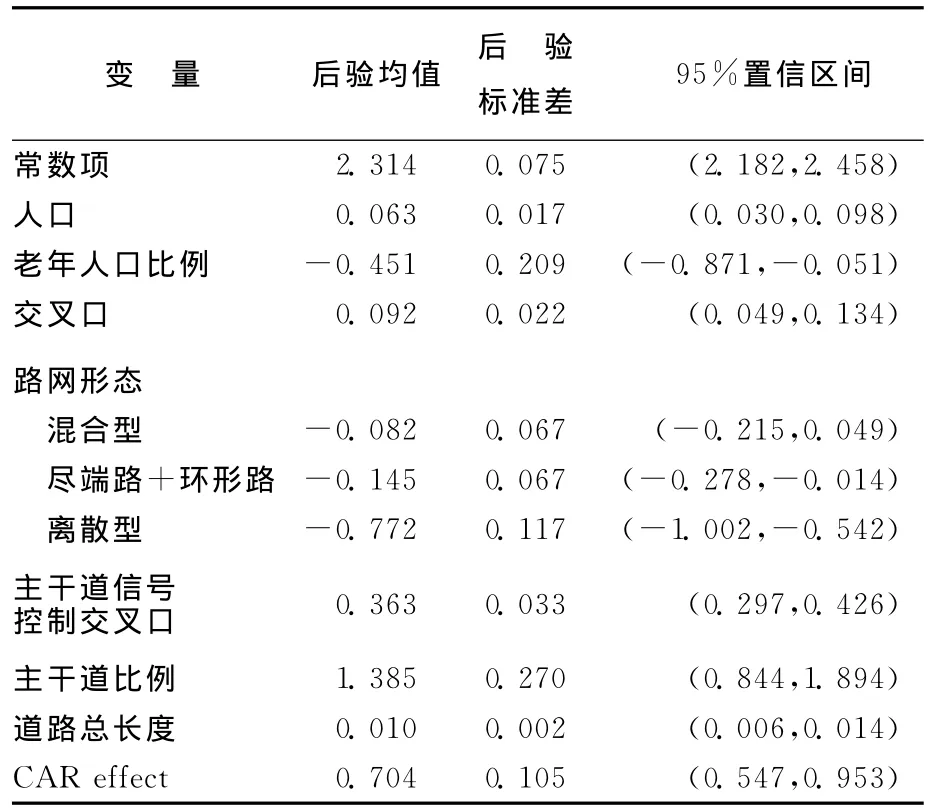
表4 贝叶斯泊松CAR模型标定结果比较

4.2.2 其他变量

除了路网形态，影响全体事故的显著因素还有主干路的比例，随着主干路比例的提升，事故发生的概率也随之增大。这与之前有研究认为高等级的道路长度增加会增大事故发生的可能，而地方生活性道路里程的增加则可以减少事故发生的几率是一致的［4，6，12］。主干道上交叉口数量和信控交叉口数量对事故的影响在95%显著性水平下都是显著为正的，原因可能是交叉口过于复杂的交通流及可能存在的大流量交通。车公里数VKT和道路总长度等道路交通特征属性对事故的影响也都是显著为正的。这些结论同常识是相符的，并同之前相关研究结论类似［2，4－6，26］。

此外，TAZ内人口数量对TAZ事故数量的影响在95%显著性水平下是显著为正的，这同以往研究是相似的［27］。而TAZ内老年人口比例对TAZ事故数量的影响显著为负，这同文献［2］研究伦敦事故发生原因的结论一致。

5 结束语

宏观交通安全建模作为交通安全规划的重要组成部分，在国内无论是理论研究还是应用实践方面已经受到越来越多的关注，也取得了一定成果［28］。本文就交通安全规划的核心技术问题——宏观交通安全建模进行了初步研究，基于美国佛罗里达州Orange县数据，在TAZ层面针对全体事故建立了贝叶斯泊松CAR模型用以分析包括路网结构特征、交通运行特征以及人口及土地利用情况在内的宏观交通安全影响因素。

另一方面，本文在很多方面仍然需要更深入的研究，文中仅考虑TAZ相邻空间关系，需要进一步研究TAZ层面交通安全数据特点（例如TAZ距离远近等），开发更有效的宏观交通安全分析模型。下一步的研究还包括道路网络的等级结构、布局结构对交通安全的影响，在传统交通规划的哪个阶段、以何种方式接入宏观交通安全分析等。

［1］Ned L，Karl E K，Lawrence H N.Spatial analysis of Honolulu motor vehicle crashes：Ⅰ，spatial patterns［J］.Accident Analysis and Prevention，1995，27（5）：663－674.

［2］Quddus M A.Modelling area－wide count outcomes with spatial correlation and heterogeneity：an analysis of London crash data［J］.Accident Analysis and Prevention，2008，40（4）：1486－1497.

［3］Dominique L，Bhagwant N P.Estimating the safety performance of urban road transportation networks［J］.Accident Analysis and Prevention，2004，36（4）：609－620.

［4］Lovegrove G R，Sayed T.Macro－level collision prediction models for evaluating neighborhood traffic safety［J］.Canadian Journal of Civil Engineering，2006，33（5）：609－621.

［5］Khondakar B，Lovegrove G R，Sayed T，et al.Transferability of community－based macro－level collision prediction models between different time－space regions for use in road safety planning applications［C］／／88th Transportation Research Board Annual Meeting，Transportation Research Board，Washington，D C，2009：09－0610.

［6］Hadayeghi A，Shalaby J，Persaud B N.Macrolevel collision prediction models for evaluating safety of urban transportation systems ［J］.Transportation Research Record：Journal of the Transportation Research Board，2003：1840：87－95.

［7］Ng K，Hung W，Wong W.An algorithm for assessing the risk of traffic accident ［J］.Journal of Safety Research，2007，33（3）：387－410.

［8］Guevara F L D，Washington S P，Oh J.Forecasting crashes at the planning level：simultaneous negative binomial crash model applied in Tucson，Arizona［J］.Transportation Research Record：Journal of the Transportation Research Board，2004，1897：191－199.

［9］Lovegrove G R，Lim C，Sayed T.Using macrolevel collision prediction models to conduct road safety evaluation of regional transportation plan［C］／／87th Transportation Research Board Annual Meeting，Transportation Research Board，Washington，D C，2008：08－0693.

［10］Haynes R，Jones A，Kennedy V，et al.District variations in road curvature in England and Wales and their association with road－traffic crashes［J］.Environment and Planning：A，2007，39（5）：1222－1237.

［11］Sun J，Lovegrove G R.Using community－based macrolevel collision prediction models to evaluate safety level of neighborhood road network patterns［C］／／89th Transportation Research Board Annual Meeting，Transportation Research Board，Washington，D C，2010：10－0535.

［12］Hadayeghi A，Shalaby A，Persaud B.Development of planning－level transportation safety models using full Bayesian semiparametric additive techniques ［J］.Journal of Transportation Safety ＆Security，2010，2（1）：45－68.

［13］张春平，景天然.城市道路交叉口交通安全评价研究［J］.同济大学学报：自然科学版，1994，22（1）：47－52.

［14］裴玉龙，马 骥.道路交通事故道路条件成因分析及预防对策研究［J］.中国公路学报，2003，16（4）：77－82.

［15］裴玉龙，马艳丽.寒冷地区城市道路交叉口条件与交通事故关系［J］.哈尔滨工业大学学报，2005，37（1）：130－133.

［16］成 卫，丁同强，李 江.道路交叉口交通冲突灰色评价研究［J］.公路交通科技，2004，21（6）：97－100.

［17］缪玉玲，陈小桐，李 峰，等.引入交通安全对交通规划的新思考［C］／／中国公路学会.第二届全国公路科技创新高层论坛论文集：上卷，北京，2004.

［18］王 岩，杨晓光.主动道路交通安全规划体系［J］.系统工程，2006，24（1）：30－35.

［19］唐珏琳.城市规划中的交通安全因素分析［J］.公路与汽运，2007（4）：47－48.

［20］Buhl J，Gautrais J，SoléR V，et al.Efficiency and robustness in ant networks of galleries［J］.The European Physical Journal：B 2004，42（1）：123－129.

［21］Southworth M，Ben－Joseph E.Streets and the shaping of towns and cities ［M］.Washington D C：Island Press，2003：40－72.

［22］茆诗松.贝叶斯统计 ［M］.北京：中国统计出版社，1999：26－83.

［23］Lynch S.Introduction to applied Bayesian statistics and estimation for social scientists［M］.New York：Springer Science＋Business Media，LLC，2007：47－53.

［24］Gelman A，Hill J.Data analysis using regression and multilevel／hierarchical models ［M］.Cambridge：Cambridge University Press，2006：281－334.

［25］Guo F，Wang X，Abdel－Aty M.Modeling signalized intersection safety with corridor－level spatial correlations［J］.Accident Analysis and Prevention，2010，42（1）：84－92.

［26］Hadayeghi A，Shalaby A S，Persaud B N.Development of planning level transportation safety tools using geographically weighted Poisson regression［J］.Accident Analysis and Prevention，2010，42（2）：676—688.

［27］Noland R B，Quddus M A.A spatially disaggregate analysis of road casualties in England ［J］.Accident Analysis and Prevention，2004，36（6）：973－984.

［28］金 昱.基于贝叶斯空间统计分析的宏观交通安全研究［D］.上海：同济大学，2010.