电力推进船舶中永磁电机直接转矩控制
2011-08-28郭昊昊刘彦呈任俊杰
郭昊昊, 刘彦呈, 任俊杰
(大连海事大学轮机工程学院,辽宁大连 116026)
0 引言
产生于20世纪80年代的直接转矩控制理论起初被应用于三相交流异步电机的调速中[1-2],随后国外学者对永磁电机直接转矩控制理论进行了分析研究[3],而1995年由瑞士ABB公司研制的采用直接转矩控制的变频器已应用于船舶电力推进中。传统直接转矩控制采用两点Bang-Bang滞环控制器输出控制信号,通过预制的开关表选取合适的电压空间矢量,来分别实现对定子磁链和电机转矩的控制[4-7]。直接转矩控制中取消了电流控制环,同时在模型中只需要电机定子的电阻值,降低了电机参数的依赖性,电机转矩的动态响应时间较短,因此比较适用于需要快速动态转矩响应的船舶电力推进系统。
本文以烟大铁路轮渡1号船舶中的主推进永磁电机为研究对象,该电机额定功率4 088 kW,额定电压660 V,额定电流4 348 A,额定转速200 r/min,额定转矩195 200 N·m。通过对永磁电机直接转矩控制的理论分析,建立了基于传统开关表的船用大功率永磁电机直接转矩控制仿真模型,对仿真结果进行了分析与研究。
1 永磁同步电机数学模型
在建立数学模型前,先做如下假设:忽略铁心饱和,不计涡流和磁滞损耗;永磁材料的电导率为零;转子上没有阻尼绕组;相绕组中感应电动势波形为正弦;忽略电机运行时的摩擦系数。由此可得永磁同步电机在同步旋转坐标系d-q轴系下的数学模型为

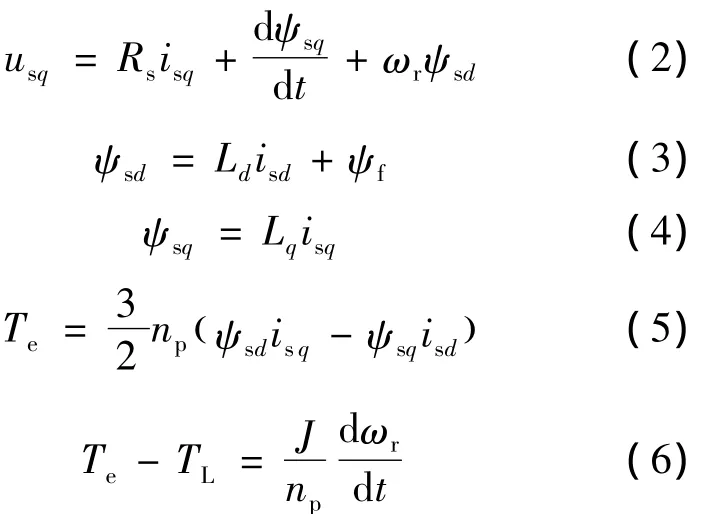
式中:usd,usq——同步旋转坐标系d-q轴系下的电机电压;
isd,isq——同步旋转坐标系d-q轴系下的电机电流;
Ld,Lq——同步旋转坐标系d-q轴系下的电机电感;
ψsd,ψsq——同步旋转坐标系d-q轴系下的电机磁链;
Rs——定子绕组相电阻;
ωr——转子电角速度;
ψf——永磁体磁链幅值;
np——极对数;
Te——电磁转矩;
TL——负载转矩;
J——电机及其负载的转动惯量。
2 直接转矩控制理论分析
2.1 永磁同步电机直接转矩控制的基本思想
永磁同步电机直接转矩控制采用的是定子磁链定向控制,根据定子磁链坐标系下的数学模型,经过坐标变换可得其电磁转矩的表达式为

式中:ψs——电机定子磁链值;
ψf——转子永磁体磁链值;
δ——电机功角。
由式(7)可看出,如果通过一定控制策略保持定子磁链幅值|ψs|恒定,假设永磁电机转子磁链幅值、Ld、Lq恒定,电机的电磁转矩就由定、转子磁链夹角δ决定,可以通过改变定、转子磁链夹角的大小来改变永磁同步电机转矩的大小。
2.2 直接转矩控制中定子磁链幅值与转矩控制
估算电机定子磁链时,若定子磁链的初始值为零,则有:

忽略定子电阻压降,则由式(8)可得:
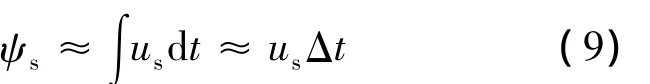
从式(9)可看出,当电机定子上作用一个电压空间矢量us,定子磁链矢量ψs将产生一个沿着电压空间矢量us方向的增量,或者说定子磁链矢量的顶点将沿着该电压空间矢量所指的方向移动,定子磁链幅值的变化由|us|的大小和作用时间Δt决定,方向与该电压空间矢量作用前的ψs方向不同,取决于电压空间矢量us的方向。电压空间矢量us作用于定子绕组Δt时间后,总磁链ψsi应为原来磁链值和磁链变化值的矢量和,即:

这就说明可以通过控制永磁同步电机的输入电压空间矢量us来精确控制定子磁链的幅值、旋转方向及旋转速度。
图1所示为电压型理想逆变器的示意图,开关Sa与称为a相开关,当Sa闭合时a相上桥臂与电源正极接通,用“1”表示,Sa断开时用“0”代表。Sa与互为相反,即当 Sa为“1”时为“0”;Sa为“0”时为“1”。b、c两相的定义与 a相同。

图1 电压型理想逆变器
表1为逆变器的8种开关组合,8种可能的开关状态可分为两类:一类是6种所谓的工作状态,即表1中的状态“1”到状态“6”,它们的特点是三相负载并不都接到相同的电位上去;另一类开关状态是零开关状态,如表1中的状态“0”和状态“7”,它们的特点是三相负载都被接到相同的电位上去。当三相负载都与“+”极接通时,得到的状态是“111”,三相都有相同的正电位,所得到的负载电压为零。当三相负载都与“-”极接通时,得到的状态是“000”,负载电压也都是零。

表1 逆变器的八种开关组合
由逆变器的状态1到状态6这6种开关组合,可以得到6个离散的电压空间矢量us,每两个电压空间矢量在空间的位置相隔60°角度,图2为电压空间矢量的分布图。

图2 电压空间矢量分布图
由图2可知,当定子磁链在不同区间时,可通过选择不同的电压空间矢量对定子磁链进行控制,在保持磁链幅值为恒定值的前提下,同时使其旋转轨迹近似为圆形。
在直接转矩控制中,电机定子磁链幅值通过上述电压空间矢量的控制,可保持为恒定值,要改变电磁转矩的大小,需要通过控制定、转子磁链之间的夹角即功角来实现。通过对定子磁链的限幅控制,就能获得近似圆形旋转的定子磁链,由于转子的机械时间常数远大于电气时间常数,在定子磁链旋转的过程中,转子磁链的转动速度还没来得及发生变化,因此夹角δ的调节可通过改变定子磁链的瞬时旋转速度来实现,在实际中这又是通过选择适当的电压空间矢量,使定子磁链顺时针方向旋转或逆时针方向旋转,从而改变定、转子磁链间夹角δ的大小,最终达到改变电机电磁转矩的目地。图3为直接转矩控制系统框图。

图3 传统直接转矩控制系统框图
该系统只需检测电机三相电流与逆变器端的直流母线电压,由直流母线电压和开关表Sabc的值可得定子三相电压值,测得的电流与电压经过3/2坐标变换得到两相静止坐标系下的电流与电压信号,从而估算得到电机内部实际的定子磁链、电磁转矩、磁链位置角θs。给定转速与实测电机转速经过比例积分调节后得到电机参考转矩的给定信号Teref,参考转矩Teref与转矩估算模块得到的实际转矩Te之差,经过转矩滞环调节,得到是否需要增大转矩或者减小转矩的信息;同时估算得到的定子磁链与给定磁链的差值经过磁链滞环调节,得到是否需要增大磁链或者减小磁链,再结合定子磁链所处的扇区,选择合适的电压空间矢量,控制逆变器中的开关状态,进而控制电机的运行。
3 仿真及结果分析
本文采用MATLAB/Simulink工具箱对烟大铁路轮渡电力推进船舶中大功率永磁同步电机直接转矩控制模型进行仿真分析。仿真对象的具体参数如下:额定功率4 088 kW,额定电压660 V,额定电流 4 348 A,极对数为 8,额定转速200 r/min,额定转矩195 200 N·m。
(1)模拟实际船舶定速航行时,遇到突发事件,负载转矩发生突变的工况,仿真时间为2 s。0 s时电机处于静止状态直接给一个转速阶跃信号,阶跃值为120 r/min,电机的初始负载转矩为120 000 N·m,在1.0 s时负载转矩突加为电机的额定转矩195 200 N·m。采用传统开关表直接转矩控制策略的仿真结果如图4~图6所示。
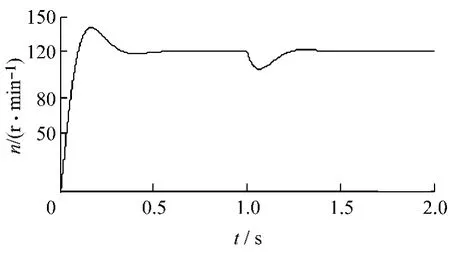
图4 电机转速曲线

图5 电机转矩曲线图

图6 电机定子磁链轨迹曲线
从图4可看出电机的转速在很短的时间内(约0.3 s)就能稳定在转速设定值120 r/min,在1.0 s时转速发生波动,这主要是由于该时刻负载转矩突然增大所造成的,随后转速快速稳定在设定值120 r/min。从图5可看出,在约0.3 s时,电机的电磁转矩稳定在120 000 N·m,当负载转矩在1.0 s时突加为电机的额定转矩195 200 N·m时,电机产生的电磁转矩也能及时稳定在该值上。同时从图6可看出,电机定子磁链的轨迹近似为圆形,磁链幅值基本保持不变。
(2)模拟实际船舶碰到紧急情况,需要船速快速改变的工况,仿真时间为2.0 s,在负载转矩为电机的额定转矩195 200 N·m时起动电机。初始转速给定为150 r/min,在1.0 s时转速给定值改为200 r/min。仿真结果如图7~图8所示。

图7 电机转速曲线

图8 电机转矩曲线
从图7可看出,电机转速很快就能稳定在初始设定值150r/min,在1.0s时转速给定值由150 r/min突变为额定转速200 r/min,电机也能快速加速并稳定在给定值200 r/min。从图8可看出,当电机转速为稳定值时,电机电磁转矩始终保持与额定负载转矩195 200 N·m相等,只是在电机起动和给定转速发生突变时,电机电磁转矩才波动至较大值,用以完成电机的加速过程。当电机工作于额定负载转矩195 200 N·m时,电机的转速能够稳定运行在200 r/min,说明仿真结果与该电机的设计值相符合。
4 结语
本文对采用直接转矩控制的船用大功率永磁同步电机变频调速系统进行了分析,建立了基于传统开关表选择的直接转矩控制的仿真模型,仿真结果表明:电机动态转矩的响应时间很快,推进电机的加速时间较短,在很短的时间内便能稳定达到给定转速,说明采用直接转矩变频调速的控制系统适用于船舶电力推进,能够满足对推进系统动态响应时间的要求。
[1]Depenbrock M.Direct self-control(DSC)of inventerfed induction machine [J].IEEE Transactions on Powe Electronics,1988,3(4):420-429.
[2]Takahashi I,Noguchi T.A new quick-response and high-efficiency control strategy of induction motor[J].IEEE Transactions on Industry Applications,1986,22(5):820-827.
[3]Zhong L,Rahman M F,Hu W Y,et al.Analysis of direct torque control in permanent magnet synchronous motor drives[J].IEEE Transactions on Power Electronics,1997,12(3):528-536.
[4]李夙.异步电动机直接转矩控制[M].北京:机械工业出版社,2001.
[5]谢运祥,卢柱强.基于MATLAB/Simulink的永磁同步电机直接转矩控制仿真建模[J].华南理工大学学报(自然科学版),2004,32(1):19-23.
[6]林海,李宏,李小川,等.永磁同步电动机直接转矩控制策略研究[J].微电机,2007(10):28-31.
[7]张益男,刘国海.永磁同步电动机直接转矩控制的仿真与实验研究[J].微电机,2009(2):39-42.
