构建高效课堂 提高教学效率——浅谈“目标引领,活学巧用”高效课堂中的难点突破
2011-08-25510900广东省广州市从化中学杨仁宽
510900 广东省广州市从化中学 杨仁宽
构建高效课堂 提高教学效率
——浅谈“目标引领,活学巧用”高效课堂中的难点突破
510900 广东省广州市从化中学 杨仁宽
1 引言
随着课程改革的深入和新课程实施的推进,优化课堂教学环节,促进课堂教学高效,提高课堂教学质量,是学校可持续发展面临的重要课题.结合高中课程方案的要求和学校实际,在深入听课、广泛调研的基础上,学校提出了课堂教学“十二字”要求:抓本质,促兴趣,探方法,求效率.在此要求下,构建并实施“目标引领,活学巧用”高效课堂教学,取得了较好的课堂教学效果.
2 课堂教学“十二字”要求的含义
“抓本质”,就是每一堂课都要突出重点、突破难点,围绕学科的主干知识点选材并合理设计教学中的师生活动过程与内容.
“促兴趣”,就是结合教学内容创设情景,激发学习情感,培养学习兴趣.既科学、规范、严谨,又灵活、多样、有趣,充分挖掘教材的学科潜能与教育功能,设计与实施的过程,能贴近学生实际,符合年龄特点,有特色.
“探方法”,就是创设较为恰当的教学情景,选择切合实际的学习材料,运用启发式教学,引导学生探索出解决本节课课题的有效途径和较为合理的方法(即学科的通性与通法),在教学过程中,有学法指引的意识、构思与措施等,使学生学有章法,用有方法.
“求效率”,就是既要适时地设计并运用多媒体辅助教学,紧扣课题精选适当素材,课堂练习的难度与容量适中;又要整体把握课堂的各个环节,师生合作并探究、生生“质疑”并探索,提高课堂教学效率.努力达成新课程理念下“知识与能力、过程与方法、情感态度与价值观”的三维教学目标,使每位学生都获得最切合实际能力与实际水平的教育,能取得体现自我的最佳成绩.
按照上述课堂教学“十二字”要求,自2008学年起实施“构建高效课堂”方案.在“以人为本,和谐发展”的办学理念和“依本、质疑、合作、共进”的教学理念引领下,确立“目标引领,活学巧用”高效课堂教学模式,本文简介此模式,并就此模式下难点突破的策略与方法,举例给予说明.
3 “目标引领,活学巧用”高效课堂教学模式简介
课堂是实施课程改革的主阵地,构建“目标引领,活学巧用”高效课堂,提高课堂教学效益是提高教学质量的关键,是提升教师专业素养,促进其成为实践反思型教师的需要.
3.1 几个关键词
“目标引领”,就是制定合适的、高效的课堂教学目标,实施目标教学.
“活学”,就是自主学习、合作学习、探究学习的灵活选择与有效运用.
“巧用”,就是学习中的实践→思考→巩固→反思→再思考→提升的过程.
“目标引领,活学巧用”高效课堂教学模式的核心理念是“以人为本”:学生是一切学习活动的主人,是学习过程的主体,一切教学活动皆应围绕学生的学而展开.
构建并实施此教学模式,目的是为了实现课堂教与学的高效率,使学生在课堂上的思维量,接收知识的信息量和有效训练量等,实现最大化.
简介2种高效课堂课型模式如下:
3.2 “目标引领,活学巧用”新授课教学模式
树立“依本,质疑,合作,共进”的教学理念,实施目标引领下的自主学习、合作学习、探究学习,把拓展学生的思维量、接收知识的信息量和有效训练量作为主要任务;围绕学生的疑难点、易错点、易混点精讲精练;安排足够时间让学生进行针对性练习,确保课堂教学目标的有效、高效达成.
新授课教学实施与操作流程图如下:
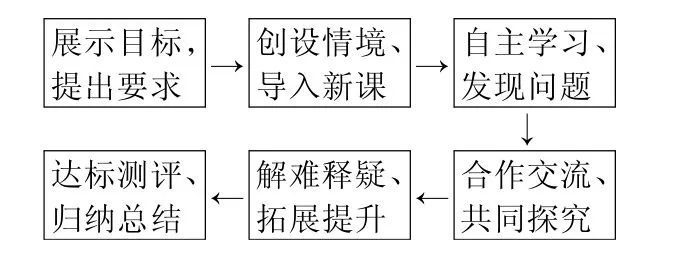
教师的作用是:设景激趣→展示目标→答疑解惑→点拨示范→精讲深化→迁移检测.
学生的任务是:自学教材(学案)→讨论质疑→测试演练→归纳总结→迁移创新.时间分配如下:
目标引领(5分钟):创设情境,引入新课,展示介绍本节课学习目标.
自主学习(10分钟):学生在目标引领下自主学习,通过自学初步了解知识架构,理解概念、规律,解决学习中的一般性问题.
合作学习(10分钟):学生相互质疑,老师适时点拨,兵教兵、兵练兵、兵正兵,兵强兵.
精讲精练(10分钟):老师根据学情设计问题,有针对性的讲解,释疑、解惑、训练.
归纳总结(5分钟):归纳知识,小结方法,提升思维,布置课后学习任务.
3.3 “目标引领,活学巧用”复习课教学模式
以高效训练为主线,使复习课的有效性“落实在笔尖上”.优化传统的“知识梳理→典型示例→巩固训练”设计架构,强调学生的动手实践,减少师生间对话式的简单回顾,主要流程如下:
诊断测试→知识梳理→典型示例→巩固训练→能力拓展→达标测验.
教师则合理安排练习与讲授时间,通过设疑激发兴趣,激活课堂;通过点拨归纳,引导学生总结和形成知识系统;通过专题训练,增强学生解题思维的灵活性和规范性,最终促使学生找出知识间的内在联系,巩固和深化所学知识,理清知识体系,建立知识网络,形成学科技能.
4 应用举例
现就上述2种课型模式,举例说明如下.
4.1 “目标引领,活学巧用”新授课实例分析
(1)求f(f(1))的值;
(2)求f(x)在[-2,4]上的最大值和最小值.
这是高一新授《对数函数》习题课中的一道例题,对于刚刚跨入高中学习时间不长的高一同学来说,可谓难点不少、难度不小!如何才能突破呢?
简析 依据“知识点的就近关联区”,设计下列递进式问题链,使难点得以各个击破:
①指数函数是如何定义的?

②如何化简题中所给出的λ?
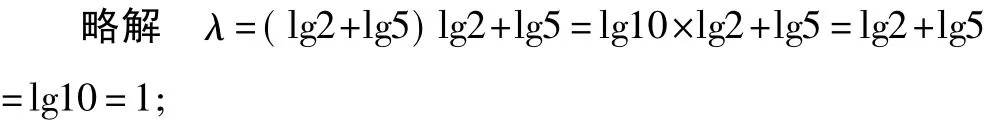
③题目中的两个函数表达式分别是什么?

⑥如何求它的最大值与最小值?
略解 由于y=f(x)的对称轴是x=2,因而它在[0,2]上单调递减,在[2,4]上单调递增,此时 f(2)=-4≤f(0)=f(4)=0;
综上可知,
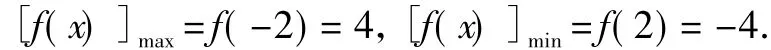
4.2 “目标引领,活学巧用”复习课实例分析
例2 (2009年广东压轴题)从点P(-1,0)向曲线Cn:x2-2nx+y2=0(n=1,2,…)Cn引斜率为 kn(kn>0)的切线 ln,切点为 Pn(xn,yn).
(1)求数列{xn}与{yn}的通项公式;
(2)证明:
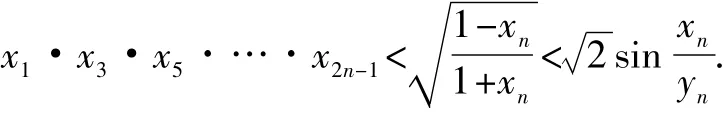
简析 作为高考压轴题,本题第(2)小题综合性强,能力要求高,其难点不容易突破.
依据“知识点的就近关联区”,设计递进式问题链,可以使难点分散突破如下:
①依据题意与条件,你会选择直线方程的哪一种形式?
略解 依照本题的条件,选择直线方程的点斜式较为有利.
②如何利用条件“ln与Cn相切”?

③由上述所求的结果,第(2)小题的待证式子,可以化简吗?

④上式可以分视为几个部分?
略解 可以视为两个不等式,先证明不等式


本题将几何与代数有机地融为一体,主要考查曲线与方程,导数及其应用,曲线的切线,数学归纳法,三角函数及其单调性,不等式的证明等等,考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用创新意识.
5 后记
我校是广州市郊区县中学,生源排列广州市第二组13所中学较后的位置,实施“目标引领,活学巧用”课堂教学模式试验3年,促进了学校更好的发展和更大的进步.如,2011年高考,所有批次上线人数刷新历史记录,并创历史新高.其中,文科上重点线人数,在广州市124所学校中列第5位;理科上重点线人数列第10位.学校连续第15年获得广州市高中毕业班工作一等奖(名列全市第4).
1 杨仁宽.创设新颖情境,体现课标理念,考查探究能力[J].中学数学.2010,8
2 杨仁宽.巧裂项求数列的和,妙放缩证明不等式[J].中学数学.2011,10
20111127)
