节点分析法及其MATLAB辅助实现

李彩萍，李乐生

（太原理工大学电气与动力工程学院，山西 太原 030024）

1 引言

节点分析法和网孔分析法是《电路分析基础》课程中两种主要的分析方法，可用于直流电阻电路及正弦稳态电路的分析求解。其中，网孔分析法适用于网孔数少于节点数的平面电路的分析，其实质是列电路中各网孔的KVL方程；节点分析法则适用于节点数少于网孔数的平面及非平面电路的分析求解，其实质是列电路中各独立节点的KCL方程。对平面电路来说，网孔分析法和节点分析法是两种对偶方法，因此，本文针对节点分析法在授课过程中学生较难掌握以及较易出错的知识点进行归纳总结，最后给出了用MATLAB软件对节点方程进行辅助求解的过程，并举例进行了详细说明。

2 节点分析法的原理

节点分析法是以节点电压为未知量，联立方程，求解各节点电压值，然后进一步求出待求量的分析方法[1]。这要求同一电路各节点电压必须是一组独立和完备的变量。以图1直流电阻电路为例，列出其节点电压方程如方程组（1）所示：

图1 节点分析法示例1

式中，G11、G22分别为节点1、节点2的自电导，节点的自电导等于与该节点相连的各电阻支路电导之和。G12、G21分别为节点1与节点2、节点2与节点1的互电导，互电导是两个相邻节点公共电阻支路的电导。方程右端为流向各节点的理想电流源电流的代数和，用isii表示；其中流入节点电流取“+”，流出节点电流取“-”。因此将图1中各元件参数代入方程组（1）可得方程组（2）。

对有N个节点的电路，同理可列出N-1个独立节点方程。

3 节点分析法的重点和难点

（1）电路中如果含有理想（或受控）电压源串联电阻支路，则根据等效变换，可将其等效变换为电流源并联电阻支路。电路中如果含有理想（或受控）电流源串联电阻支路，则根据替换定理，可将理想（或受控）电流源串联电阻支路等效变换为一个理想（或受控）电流源支路。对电流源串联电阻支路，学生在分析时容易忽视这种等效变换，在一个方程的左端既考虑了串联电阻，在同一个方程的右端又考虑了理想（或受控）电流源的电流。避免出现这种错误的有效手段，除了将理想（或受控）电流源串联电阻支路等效变换为一个理想（或受控）电流源支路方法外，还可以在理想（或受控）电流源和其串联电阻之间增加一个节点，将理想（或受控）电流源和其串联电阻看成两条支路来进行处理。

（2）参考节点的选取。由于节点分析法实质是列各个节点的KCL方程，这样对有n个节点的电路，独立节点数为n-1，根据n-1个独立节点列出的KCL方程恰好是一组独立的方程。因此在用结点分析法求解时，需要首先选定其中一个节点作为参考节点。参考节点的选取应该遵循以下几个原则：①由于人们一般习惯认为下面是地，因此在选取参考节点时，可根据人们的习惯选电路下面的节点作为参考节点。如图1中节点3恰好位于电路的下部。如果电路下方有两个或两个以上节点，则选择连接支路比较多的节点作为参考节点。②如果电路中含有理想（或受控）电压源，通常选取电压源的负极作为参考节点。这样，电压源正极对应节点的节点电压就是该电压源电压。因此不必再列写该节点电压方程。部分同学易犯的错误是不进行参考节点的选取，给所有节点都列写节点方程。

（3）如果两个独立节点之间包含一个理想（或受控）电压源支路，则在列写这两个独立节点的节点方程时，需要将该理想（或受控）电压源所在支路电流也考虑进去。如果将该理想（或受控）电压源所在支路电流放在方程左端，则流出节点电流前取“+”号，否则取“-”号。如果将该理想（或受控）电压源支路电流放在方程右端，则恰好相反。学生们易犯的错误是忽视了该理想（或受控）电压源支路流过的电流。因此授课时，应特别强调节点分析法实质是列各个节点的KCL方程，与每个和独立节点相连的所有支路电流都应该考虑。

下面以图（2）电路图为例，进一步说明以上几个难点。

首先，在该电路图中含有一个1V理想电压源串联1个3S电导，为简化分析，应将其变换为一个电流源并联电导的组合。

图2 节点分析法示例2

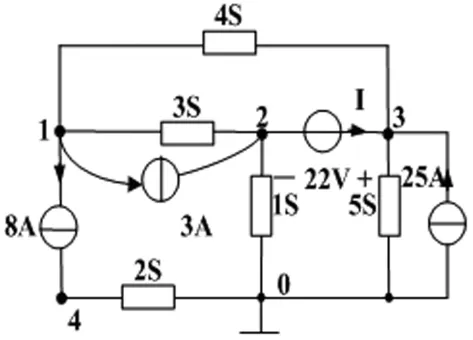
图3 节点分析法示例2分析图1

图4 节点分析法示例2分析图2

其次，在该电路图中含有一个8A理想电流源串联1个2S电导，此时可采用两种方法处理，一种方法是在8A理想电流源和2S电导之间增加一个节点4，见图3，则电路的独立节点数为4个。另一种方法是将8A理想电流源串联2S电导的组合等效变换为一个8A的电流源，见图4，此时电路的独立节点数为3个。比较简单的方法是采用图4的简化电路，这样可以减少一个节点方程。

另外，该电路如果选用节点0作为参考节点，比较符合人们的思维习惯。但此时节点2和节点3之间有一个22 V独立电压源，因此需要在电路图上标注流经22 V独立电压源电流及其参考方向。根据图 4 列写的节点方程见（3）、（4）、（5）和（6）式：

如果根据图（3）列写节点方程，则需要再增加方程（7）：

4 MATLAB软件辅助求解节点电压方程的实现

MATLAB语言是一种广泛应用于工程计算及数值分析领域的新型高级语言，其强大的数值计算功能、图形显示功能、简洁的编程语言及可交互的集成环境，深受科研工作者及工程技术人员的欢迎。

用MATLAB进行电路理论的辅助分析，主要包括3种方法[2]：第一种是先通过手工建立电路方程，再借助MATLAB强大的数值计算功能求解已建立的电路方程。第二种是利用节点支路关联矩阵和支路VAR[3]，通过矩阵运算推导出节点方程，但这种方法需要利用电路的拓扑图，因此建立节点方程的过程比较繁琐。第三种方法是采用符号电路分析，可用于电路设计时确定元件的参数。下面以第一种方法为例，说明采用MATLAB求解采用前述方法已建立的电路方程的详细过程。

设已建立的电路方程如式（8）

其中：x是由电路中的一些电压或和电流变量构成的列向量；A为系数矩阵，取决于电路元件的值；B为右端列向量，其元素与电压源的电压和电流源的电流有关。则用MATLAB求解该方程的指令为

下面给出求解节点电压方程（3）、（4）、（5）、（6）中未知变量U1、U2、U3及I的程序：%node.m；求解节点电压方程的node.m程序U=zeros(4，1)；%对代求变量进行初始化，其中代求变量为U1、U2、U3、I。

A=[7-3-4 0；-3 4 0 1;-4 0 9-1;0-1 1 0]；%建立系数矩阵A。

B=[-11；3；25；22]；%根据方程右端参数建立矩阵 B。

U=AB

输入程序后点击运行按钮，则在MATLAB COMMAND WINDOW界面显示如下结果：

则 U1=-4.5 V、U2=-15.5 V、U3=6.5 V、I=51.5 V。

用MATLAB辅助求解线性代数方程的优势不是很明显，但在求解以复数为变量且方程前面的系数也是复数的节点电压相量方程时的优势就比较显著。以图5为例进行说明。

图5 正弦稳态电路的节点分析法示例

图6 图5的等效相量模型

图6选下面节点0作为参考节点，则在节点2、3之间有一个受控电压源，因此需要在图中标注出流经该受控电压源的电流及其参考方向。根据图6列写相量形式的节点电压方程：

观察发现，5个方程中有6个未知变量，这正是由于电路中含有受控电压源，对含有受控电压（电流）源的电路，一般需要根据受控电压（电流）源控制量所在支路再增加一个方程，该电路中控制量为为流经 2Ω 电阻电流，因此根据电阻 VAR可得式（15）：

联立（10）-（15）式可求解出各节点电压的相量形式。如果直接用手工求解该复数方程组，其计算量是比较大的，且易出错。下面给出用MATLAB辅助求解该方程组的程序：%node1.m；求解节点电压方程的node1.m程序U=zeros(6,1);%对代求变量进行初始化，其中代求变量为

a11=1；a21=-1/20；a22=1/20+1/2+1/（-i×2）；a23=1/（i×2）；a24=1；a32=1/（i×2）；

a33=1/2；a34=-1/2；a35=-1；a44=1；a52=1；a53=-1；a56=-5；a62=1/2；a66=-1；

A=[a11 0 0 0 0 0；a21 a22 a23 a24 0 0；0 a32 a33 a34 a35 0；0 0 0 a44 0 0；0 a52 a53 0 0 a56；0 a62 0 0 0 a66]；%建立复数系数矩阵A

B=[2；0；1；4×i；0；0]；%建立复数矩阵 B

U=AB

输入程序后点击运行按钮，则在MATLAB COMMAND WINDOW界面显示如下结果：

5 小结

节点分析法是电路理论中的一种重要的分析方法，本文首先介绍了节点分析法的原理，然后分析了用节点分析法分析电路的重点和难点，最后通过示例给出了用MATLAB辅助求解节点电压方程的详细过程。

[1]史健芳，陈惠英.电路基础.北京：人民邮电出版社，2006.

[2]赵录怀，杨育霞，张震.电路与系统分析-使用MATLAB.北京：高等教育出版社，2004.

[3]于舒娟，史学军.Matlab应用于大规模电网络的节点分析法.现代电子技术，2009：17（304），P121-123.