分部积分推广公式的应用

崔立功

（江苏财经职业技术学院基础部 江苏 淮安 223005）

0 引言

分部积分是重要的积分方法之一，可以用来求两类不同的初等函数乘积的积分。可对于面对形如 ∫un（x）eaxdx，∫un（x）sinbxdx， ∫eaxsinbxdx，（其中 a,b 是不为零的常数， un（x）是x的多项式）的积分时按照传统方法必须连续的使用分部积分法公式 ∫udv＝uv－ ∫vdu

当n较大的时候虽然能算出结果，但是过程较为复杂，计算量大，式子较多容易出错。因此运用一种分部积分推广公式不仅思路清晰，而且不易出错，所以这是个不错的方法。

1 重要的结论

下面给出两个定理和一个推论

定理 1：（分部积分推广公式）设函数 u（x），v（x）在定义区间上有n+1阶的各阶导数，则

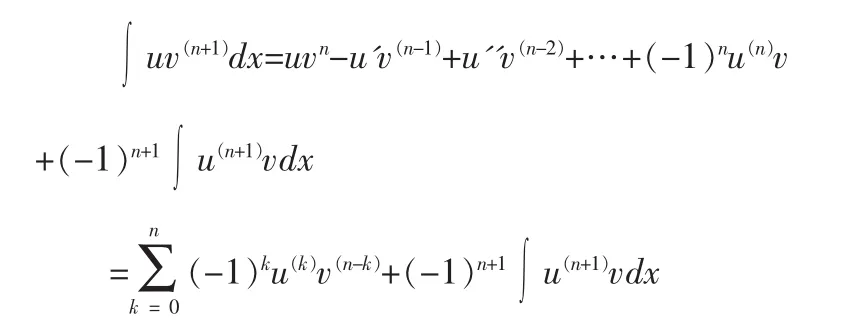
证明：当n＝0时上式即为分部积分公式当n≥1时由分部积分公式可得

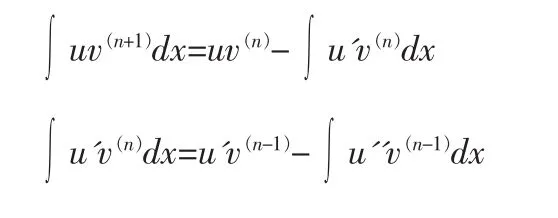
把上面的n+1个式子从下向上代人就可以得到分部积分法的推广公式

推论：如果 u（x）是 n 次多项式，v（x）是指数函数时，则

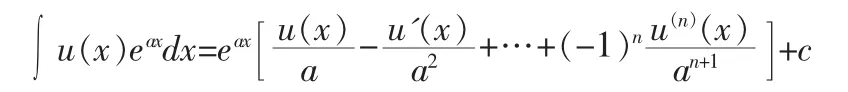
证明：令 eax＝v（n＋1）代人到分部积分的推广公式得

定理 2：设函数 u（x）是指数函数，v（x）是三角函数时，则

证明：

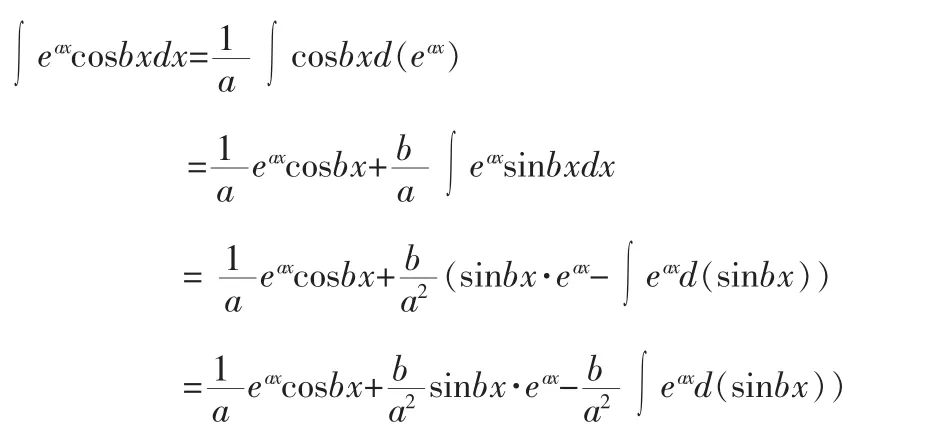
同理可以证明。

2 应用

例1求不定积分 ∫(x2+2x+3)sin2xdx

解：令 u=x2+2x+3，v（n+1）=sin2x

由分部积分推广公式得

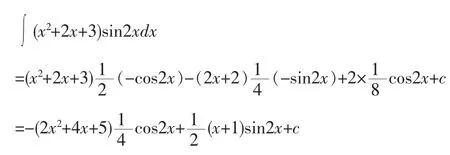
例2求不定积分 ∫(x3+x2+2x)e2xdx

解：令 u=x3+x2+2x，v（n+1）=e2x

由分部积分推广公式的推论得

3 结语

以上是笔者在多年的教学实践中总结出来的一点心得，如果两个有n+1阶各阶导数的初等函数中间有对数函数或者有反三角函数等等可以通过变量的代换然后再次用这个推广公式也是可以的这里就不再详细说明。

［1］陈光曙.大学文科数学.2版.同济大学出版社,2009.

［2］侯风波.高等数学.2版.高等教育出版社,2003.