万向铰传动偏斜轴系横向振动的主共振分析
2011-08-20冯昌林朱拥勇王德石
冯昌林,朱拥勇,王德石
(海军工程大学兵器工程系,湖北 武汉 430033)
0 引 言
偏斜轴系在各种舰艇机械结构中广泛存在,考虑用万向铰(万向联轴器)运动约束描述一类轴系的偏斜。由于万向铰的运动传输特性,即使在主动轴转速和输入力矩恒定的定常工况下,从动轴依然表现出波动的转速,承受波动的传递弯矩和轴向转矩的作用,从而引起轴系的非线性振动[1]。1958年,Rosenberg曾采取具有集中转子质量的均匀无质量弹性轴模型对万向铰传动的旋转轴的横向振动稳定性进行过研究[2],得到了偏斜角导致的各种亚临界失稳条件,研究成果至今仍得到学术界的普遍重视。结果同时表明,振动的稳定性依赖于传递力矩的幅度。T.Iwatsubo与M.Saigo,研究了弹性支撑下的有非跟随力矩作用的刚性轴,将几何约束处理为0偏斜角度,即类似于直轴,而考虑万向铰约束下的运动波动,给出了力矩表达式,发现了参数失稳和颤振型失稳;并在广义坐标的选择方法上,给出了万向铰驱动轴横向振动的Euler坐标描述方法[3]。与此同时,H.Ota,M.Kato与H.Sugita等发表了2部研究报告[4-5],导出了万向铰约束中的波动力(力矩),研究了约束激励下的横向强迫振动机理与规律,给出了特征参数的实验研究结果。其后,又进一步考虑了摩擦[6],将轴系中的从动轴考虑为无质量、偏心且对称的转子,将轴柔性处理为集中刚度,研究了参数共振问题,得到主轴转速接近于扭转、或者横向固有频率的偶数倍时,产生参数共振。尽管由于研究过程中做了较多假设,还存在进一步的待研究空间,Rosenberg[2]与T.Iwatsubo[3]的工作仍然成为研究万向铰传动轴系横向振动与稳定性的经典成果,对本文的模型研究也具有参考价值。本文将研究万向铰传动的刚性旋转轴横向振动的主共振问题。应用希尔无限行列式方法对万向铰传动的从动轴的横向振动微分方程进行稳定性分析,得到系统主共振的稳定图,并分析系统参数对主共振稳定性边界的影响。
1 模型描述
取单万向铰传动的偏斜轴系,系统包括主动轴、从动轴和万向铰十字轴。只考虑存在万向铰固有结构偏斜时,驱动轴与从动轴处于同一平面内,且2轴之间的夹角用 φ表示。当驱动轴转动时,在万向铰的作用下,从动轴产生横向振动,如图1所示,用广义坐标(角位移)αL和 βL描述从动轴的横向振动。
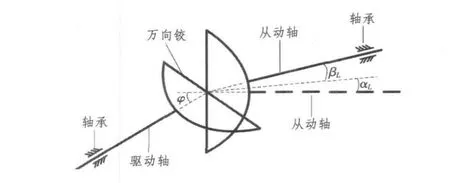
图1 偏斜旋转轴横向振动的广义坐标Fig.1 The sketch map of lareral vibration on mialigned rotary shaft
2 运动方程
本文主要研究偏斜轴系的横向振动,因此忽略从动轴的扭转弹性。从动轴受到的外力主要包括2个部分:一是万向铰十字架作用在从动轴上的力,这些力共同产生的合力矩就是主动轴输入力矩通过万向铰传递到从动轴上的力矩;二是轴承处的弹簧力和阻尼力,分别对从动轴作用产生弹簧力矩和阻尼力矩。万向铰传动偏斜轴系的横向振动可以看成是从动轴在外力矩的作用下绕万向铰十字轴的中心的转动。利用改进的从动轴绕原点转动的普遍运动微分方程(即欧拉方程),可以建立该万向铰传动的从动轴的横向振动微分方程:

其中:T0为主动轴上的输入力矩;l为从动轴长度;J0为从动轴横向转动惯量;κ为从动轴的极向转动惯量和横向转动惯量的比值;Kx2和Ky2为从动轴端部轴承处弹簧刚度系数;Cx2和Cy2为从动轴端部轴承处阻尼器阻尼系数;p(τ)为万向铰传递的角速度波动函数。
方程(1)左边第2项的系数矩阵为阻尼矩阵,阻尼矩阵中的元素有的是常数,由系统参数决定,有的是变量,与无量纲时间 τ有关;左边第3项的系数矩阵为刚度矩阵,刚度矩阵是常数矩阵,只与系统参数有关;左边第4项不含无量纲时间 τ的函数,仅与横向振动本身有关,故它能引起系统的自激振动,产生颤振型失稳;左边第5项和第6项含有无量纲时间 τ的正弦、余弦函数,作为参数激励,能引起系统的参数共振;方程右边为强迫振动项,它能引起系统的强迫共振,方程左边第4~6项及右边项都含有从动轴受到的弯曲力矩,它们均与主动轴输入力矩T0有关,是对由万向铰传递力矩引起从动轴横向振动的定量描述。可见,对于万向铰驱动的偏斜轴系横向振动问题,万向铰传递力矩不仅能引起系统的自激振动,还能引起系统的参数振动。
3 稳定性分析
令 φ=0,采用希尔无限行列式方法[3]进行主共振稳定性分析。将方程(1)对应的齐次方程组中的三角函数表示成复数形式:
由于式(1)中三角函数的周期T*=π,设式(2)解的形式为:
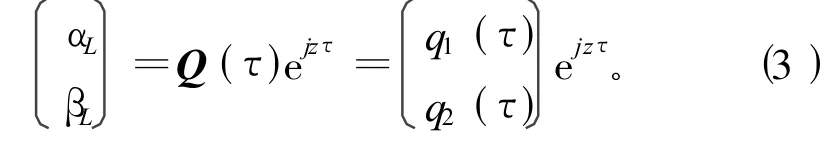
其中,Q(τ)=[q1(τ),q2(τ)]T为复周期函数,其周期为T*或2T*。由此,可将Q(τ)展开为傅立叶级数形式:
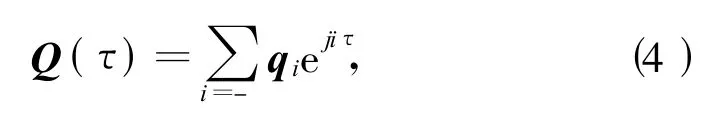
其中,向量qi=(qi1,qi2)T,且当其周期为T*,有qi=0(i=±1,±3,±5,……)。方程(2)的解可表示为:
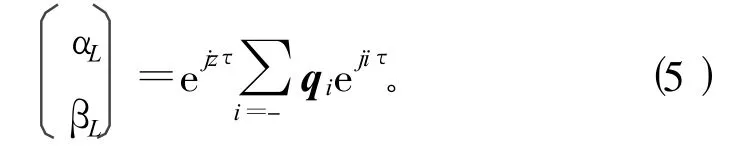
将式(5)代入式(2)中,得到如下2个关系式:
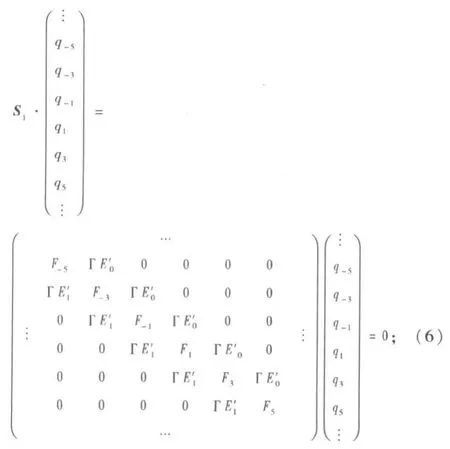
其中 ,Fi(z)=- ν2(z+i)2I+j(z+i)ν C+K+Γ E2(i=0,±1,±2,±3,±4, ±5, ±6,…);S1和S2为无穷阶矩阵。则式(2)的解为非零解的充要条件为:
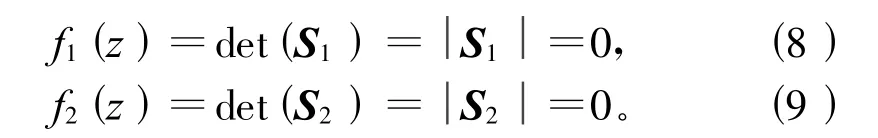
即式(2)存在非零解时必须满足矩阵S1和S2的行列式均为0。由于f2(z)=f1(z+1),说明式(8)和式(9)是等价的,分析系统稳定性,只需对式(8)或者式(9)进行稳定性分析即可。由于式(8)中既含有参数振动项和,又含有自激振动项 E2,因此,式(8)可同时给出参数激励与自激振动共同作用时的稳定性条件。
为便于计算,可将无穷维矩阵S1近似为有限维n阶矩阵进行稳定性分析,阶数越高,则所得稳定性结果与理论结果越相近。当驱动轴旋转角频率 ω接近于主共振频率 ω10时,无穷维矩阵S1近似为2阶矩阵,其相应的行列式写为:
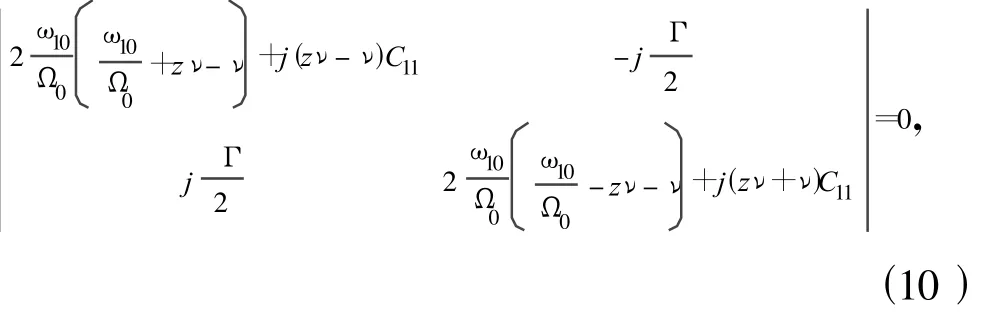
可得系统主共振(产生在固有频率 ω10处)时的稳定性条件:
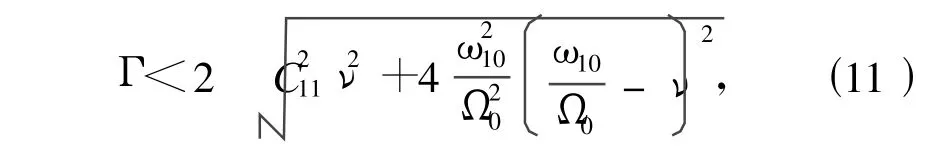
或者
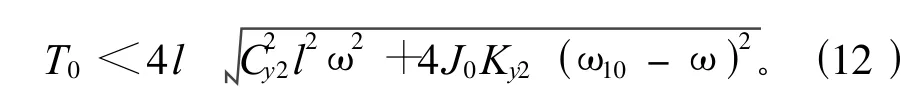
从式(11)和式(12)可以看出,主共振稳定性条件不仅与输入扭矩T0、支撑轴承安装位置l以及轴承刚度Ky2有关,还与阻尼系数Cy2以及从动轴转动惯量J0等因素有关,通过合理选取系统参数,减小系统的不稳定区,可以达到抑制系统主共振的产生。
同样,当主动轴角速度 ω接近于主共振频率 ω20时,系统主共振(产生在固有频率 ω20处)稳定性条件为
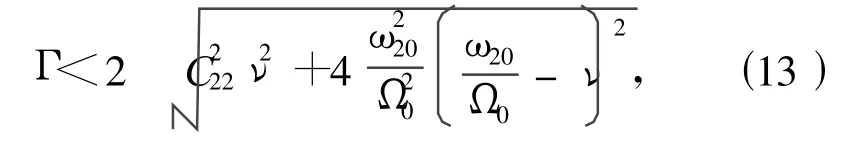
或者
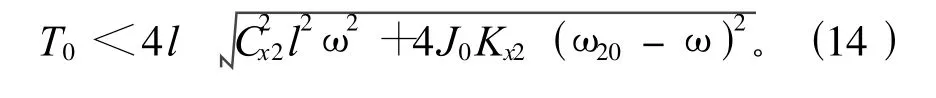
分析系统参数对主共振稳定性边界的影响。以固有频率 ω10作为中心频率时,根据式(12)可知,若输入扭矩T0一定,增大支撑轴承弹簧刚度系数Ky2与阻尼系数Cy2,增大从动轴转动惯量J0或者增大轴长l,均可使主共振的不稳定区变大,系统在频率 ω10附近易产生主共振。以固有频率 ω20作为中心频率时,也存在同样的规律。因此,在实际万向铰传动的偏斜轴系中,要抑制系统主共振的产生,应适当选择支撑轴承的安装位置,并尽量选取大刚度且足够光滑的支撑轴承,同时减小从动轴转动惯量J0。
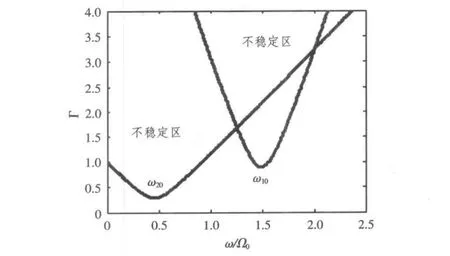
图2 系统主共振稳定图Fig.2 Stability of principal resonance
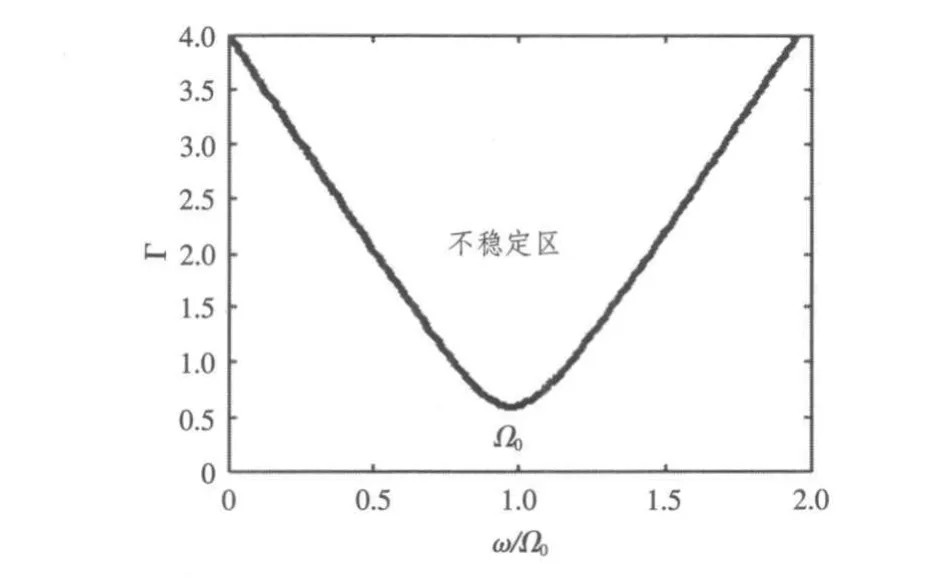
图3 主共振稳定图(Kx2=Ky2)Fig.3 Stability of principal resonance(Kx2=Ky2)
若支撑轴承具有均匀性,则Kx2=Ky2,此时有ω10=ω20=Ω0,同样取C11=C22=0.3,则根据式(11)或式(13)可得到系统产生主共振时的稳定图,如图3所示。此时,由于两固有频率相同,系统主共振时只存在1个不稳定区,其中心频率为 Ω0;注意到(ω10+ω20)/2=Ω0,这说明系统在Kx2=Ky2时产生的主共振即为系统的和型组合共振。
4 结 语
偏斜轴系的振动是机械科学及力学领域的重要研究内容。本文在考虑万向铰结构偏斜,将从动轴当作刚性细长轴,将从动轴端部支撑轴承简化为2对弹簧阻尼器的基础上,建立了万向铰传动偏斜轴系的横向振动微分方程。应用希尔无限行列式方法对方程进行了稳定性分析,得到了系统主共振的稳定图,并分析了系统参数对主共振稳定性边界的影响。结果表明,增大支撑轴承弹簧刚度系数与阻尼系数、增大从动轴转动惯量或者增大轴长,均可使主共振的不稳定区变大,系统在固有频率附近易产生主共振;系统在支撑均匀(Kx2=Ky2)时产生的主共振即为系统的和型组合共振。研究工作对进一步确定万向铰传动的偏斜轴系的动力学行为,抑制偏斜轴系振动具有重要的意义。
[1]冯昌林,王德石,等.变工况条件下万向铰驱动轴的运动特性分析[A].数学力学物理学高新技术交叉研究进展-2010(13)卷[C].北京:科学出版社,2010.479-484.FENG Chang-lin,WANG De-shi,etal.Kinematic characteristic analysis of shaft driven by universal joint in varying operating condition [A]. The Progress of Interdisciplinary Research ForMathematics,Mechanics,Physics and High New Technology,2010(13)[C].Beiing:Science Press,2010.479-484.
[2]ROSENBERG R M,et al.On the dynamical behavior of rotating shafts driven by universal(Hooke)couplings[J].ASME Journal of Applied Mechanics,1958,25(1):47-51.
[3]IWATSUBO T,SAIGO M.Transverse vibration of a rotor system driven by a cardan joint[J].Journal of Sound andVibration,1984,95(1):9-18.
[4]OTA H,KATO M.Lateral vibration of a rotating shaft driven by a universal joint-1 st report,generation of even multiple vibrations by secondary moment[J].Bulletin of JSME,1984,27(231):2002-2007.
[5]OTA H,SUGITA H,KATO M.Lateral vibration of a rotating shaft driven by a universal joint-2nd report[J].Bulletin of JSME,1985,28(242):1749-1755.
[6]KATO M,OTA H.Lateral excitation of a rotating shaft driven by a universal joint with friction[J].Journal of Vibration and Acoustics,1990,112:298-303.
