几何参数对组合式推进器流噪声水平的影响
2011-08-20周友明彭玉成
周友明,张 宁,刘 敏,彭玉成
(1.武汉第二船舶设计研究所,湖北 武汉 430064;2.华中科技大学,湖北 武汉 430074)
0 引言
泵喷是一种新型的组合式推进器,它是由环状复合导管、定子、转子、导管罩住的尾艇体结构以及轴系等共同构成。该系统新技术密集、综合集成度高,涉及到潜艇总体、性能、结构、声学、材料、轴系等众多专业领域。泵喷的工程设计与艇的总体设计呈“强耦合”关系,其设计方案不但直接影响艇的总体设计方案的成立,而且直接决定了艇的总体性能指标的实现。目前,该技术只有中、美、英、法、俄等少数大国掌握。
为了在设计阶段就能对不同泵喷设计方案的噪声特性进行比较和筛选,需要对各方案的噪声水平进行预估或者评价。如果噪声预估能达到合理的精度,还可以在此基础之上进行优化设计。但是,在目前的技术条件下,依据理论计算预估推进器的噪声不仅面临诸多技术困难,而且也是时间和人力开销很大的工作。在工程实践中,如果所有的设计工作都这样进行,代价也是相当昂贵的。因此,如果能总结出推进器几何参数对噪声水平的影响规律,用于指导设计工作,无疑可大大提高效率,降低成本。
目前,国内外学者针对螺旋桨和导管桨水动力噪声的数值预报和理论计算开展了大量的工作[1-5]。但对于泵喷这样复杂结构形式的组合式推进器的水动力噪声研究尚未见有相关文献发表。
1 噪声估算方法
1.1 声场预报面临的困难
流体内的声波,是流体质点的一种周期性运动,也可以用流体运动的基本方程组(包括动量方程、能量方程、连续性方程和物态方程)来描述。声学计算的基本方程组包括波动方程、连续性方程和物态方程,而波动方程不过是动量方程(N-S方程)的简化形式。所以,理论上,求解流体运动基本方程组的数值方法(即流场的数值计算方法,通常称为CFD方法),也可以适用于声场的计算,在采用CFD方法计算流场的同时,也可得到流体内部的声场分布。但实际上,目前的CFD方法与软件还不可能做到这一点(尽管现有的商业CFD软件已经提供了这样的功能模块[6-7])。
用现有的CFD方法计算声场所面临的第1个困难是流场的参数与声场的参数的数值相差很大。以推进器的计算为例,由叶片转动引起的流场中压力变化的数量级为105Pa,而对于水中的声场,声压级即使达到120 dB,其压力脉动幅值也只有1 Pa。显然,流场计算中由于误差所产生的压力脉动,也可能比这个幅值大得多。
鉴于这种情况,目前常用的一种方法是将流场与声场的计算分开进行。将空间划分为近场和远场2个部分。对于近场,进行动态流动计算,得到某一个人为划定的封闭曲面上各点压力的时域波形。根据基尔霍夫-海姆霍茨积分定理,该曲面上声压的面积分,即等效于曲面内的声源。这个过程是流场或称近场的计算,结果得到声源的强度。然后,在远场中假定流体为静止的,求解波动方程,即可得到接收器处声场。
但该方法只部分解决了上述困难,因为,由于流场的压力与声场的压力变化幅度相差过大,现有的流场数值计算所得到的封闭面上压力值的误差,其实已大大超过了声场的实际声压值。也就是说,这样得到的声源的强度值本身是不可靠的,因此也不可能依据此声源强度得到可靠的声场数据。
用现有的CFD方法计算声场所面临的第2个困难是湍流噪声的模拟。在处理实际的工程问题的计算中,由于受计算量的限制,通常是采用雷诺平均的方法处理湍流流场(亦即采用各种湍流模型处理湍流黏性)。显然,由于该方法仅仅计算速度和压力(在一定的尺度下)时间和空间的平均值,所以,即使是瞬态计算得到的压力的时域波动,也不能代表湍流引起的噪声声压。确实有一些文献采用这样的方法计算潜艇的噪声,但是这样的方法在逻辑上是不能成立的。
如果要得到湍流引发的噪声,只能采用湍流的直接模拟或者半直接模拟(例如大涡模拟)方法,并且网格的尺度和时间步长都必须减小到能模拟湍流中大部分漩涡的程度。这样的计算对计算资源的要求非常高,对于实际的工程问题,往往难以应用。
进一步来说,即使计算资源不成问题,考虑到前述流场与声场压力变化的数量级的巨大差别,这样计算的可靠性如何,也是难以定论的。
1.2 推进器噪声水平的评价方法
鉴于目前CFD软件还难以模拟推进器噪声源的强度,本文采用以下方法对不同参数的推进器的噪声水平进行相对比较。根据噪声产生的原因的不同,将推进器的噪声分成2部分分别处理。
1.2.1 宽带噪声
1.2.1.1 人工湍流
宽带噪声是由于湍流的脉动所产生的(在发生空化的时候,也包括空泡溃灭所产生的声波,但本文不涉及空化问题),也可以说宽带噪声源是“微观”的。由于直接模拟湍流计算量过大(而且可靠性也存有疑问),雷诺平均方法又不能模拟湍流脉动,所以本文采用人工湍流[8]的方法来评价湍流噪声的水平。采用人工湍流方法时,只需要用雷诺平均方法(采用κ-ε模型)进行静态计算,然后,用人工的方法借助一些经验或半经验的公式重建湍流的脉动速度场(不同的文献中给出的公式稍有差别)。
将流场中的1个流体微团(在CFD计算中,可以理解为1个流体单元,即1个cell)的湍流脉动动能视为由N个频率分量组成的波动信号,其总能量显然可以用湍流动能κ来表达:
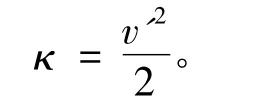
而该能量的频谱,则还与耗散率ε有关。
假定湍流为各向同性的均匀湍流,其脉动动能对于频率的能量密度用波数的函数E(α)表示(α=2πf/c0为波数,单位为 m-1;c0为音速;f为频率),Von Karman给出的密度分布如图1所示。
采用离散化的方法,将横坐标轴分为相邻的N个区间,每个区间的中心频率为αn,频带宽度为Δαn,对应的脉动速度为


图1 湍流动能的频谱Fig.1 Turbulence kinetic energy spectrum
而1个单元的湍流脉动速度为各频率分量的总和:

式中:e为单位向量;φ为初相位;ω为圆频率。φ值和e的方向均为随机的,其分布规律应保证所重建的湍流为各向同性。
关于密度函数E(α)的表达式,不同文献给出的稍有差别。本文采用的计算软件(Star-CD)中,取如下表达式:

式中,ν为流体的运动粘性系数。
1.2.1.2 宽带噪声模型
本文采用以下2种宽带噪声模型来根据湍流强度计算噪声的声源强度:
1)Proudman公式

式中:PA为单元声功率的体积密度,W/m3;ρ0为流体密度;Mt=为湍流马赫数。修正系数αε的值在计算中取为0.1。
2)Lilley模型
在忽略粘性和传热的条件下,从连续性方程和动量方程推导所得的Lilley方程为:

其中,c0为音速,而

上式的右端即为声源项。v为总速度(即包括平均值和脉动值)。进一步将脉动值分离出来并略去较小的项,可将声源简化为:

这样,声源项就仅仅包括脉动速度而不包括平均速度了。而脉动速度可以通过人工湍流方法获得。
Star-CD可以在计算结束后直接给出各单元的式(2)中声源项 S的数值(Aeroacoustic Lilley Source,AALS)。Star-CD并不提供Proudman模型,实际计算中,只能得到各单元的AALS,κ和ε的值,然后采用自编的程序按式(1)计算PA,最后,将各单元的声源功率密度(AALS和PA)乘以单元的体积后求和,即可得到推进器宽带噪声的总强度(总声功率)。
1.2.2 线谱噪声
初看起来,线谱噪声的处理应该比较容易,因为计算所要求的空间和时间分辨率都相对较低,目前的硬件水平可以支持用CFD软件采用瞬态RANS方法对推进器这样的对象进行计算。将计算得到的固壁表面的压力(时域数据)作为边界条件,用声场分析软件就可以得到推进器周围的声场。但实际上,问题远非这样简单。在目前的条件下,上述方法面临以下2个问题:
1)最大的困难仍然是CFD计算的精度难以满足声场计算的要求。
2)对于推进器这样的对象,由于叶片的形状复杂,在流场计算中,要求较高的空间分辨率。而在声场计算中,空间分辨率与时间分辨率是相关的。为满足这样高的空间分辨率,必须要有很高的时间分辨率,这样就导致计算量急剧增加。
为避免上述困难,本文并不直接计算声场,而是以作用于推进器上总作用力的脉动幅值作为评价线谱噪声的指标。这个方法其实在螺旋桨领域早已得到应用。从声学的观点来看,就是将推进器视为一个偶极子声源,其所产生的声场的强度与作用在偶极子上的交变力的幅值成正比。
这样做一方面由于不进行声场的计算,从而避免了空间分辨率和时间分辨率之间的矛盾;另一方面,在将固壁上各单元的作用力累加求和时,各单元上的微元作用力本身所具有的误差在很大程度上相互抵消(因为各单元作用力的误差是随机的,其方向和相位各不相同,故可以相互抵消)。
2 推进器几何参数与噪声水平的关系
正如前面所指出的,目前尚无法用计算的方法得到可靠的噪声数值,但用以上3个指标对不同的设计方案进行相对比较是基本可信的。
为探求推进器几何参数与噪声水平之间的关系,计算了若干泵喷推进器的设计方案,这些方案的水动力性能相同(敞水条件下,进速和推力相同,由于效率稍有差异,故功率亦有少许差别),但具有不同的几何参数。用3个指标来衡量噪声水平的高低,用AALS和PA来衡量宽带噪声水平,用作用于各部件(定子、转子、导管和总力)的径向力的脉动幅值来衡量线谱噪声的水平。这样,就可以研究推进器参数与噪声水平的关系,从而总结出指导设计的准则。
2.1 叶片侧斜与噪声水平的关系
设计了具有不同侧斜程度的3种转子叶片。图2为3种侧斜的示意图,图中3条曲线表示各半径叶切面弦长中点的连线。3种叶片分别被称为直叶片、小侧斜和大侧斜叶片。

图2 转子叶片的侧斜Fig.2 Rotor skew
2.1.1 线谱噪声比较
图3是计算所得作用于推进器各部件径向力在X方向的分量的时域波形图。在Y方向的波形与此相同,但相位相差90°。所以,实际上径向力是1个旋转的矢量,其大小(幅值)是不变的。旋转速度为转子的转速与叶片数的乘积,即脉动频率为叶频。
如果以直叶片的声压为基准(相对值为1),则小侧斜的声压值则为0.695,大侧斜为0.222。也就是说,小侧斜叶片可以降低线谱噪声3.16 dB,大侧斜可以降低13.07 dB。
2.1.2 宽带噪声比较

图3 径向力时域波形图Fig.3 Time-domain waveform of radial forces
表1为3种叶片宽带噪声计算结果的相对比较。由表中数据可见,侧斜程度对宽带噪声的影响与线谱噪声正好相反。2种模型计算所得数据不同,但变化趋势相同,即宽带噪声水平随侧斜程度的增加而升高。但是升高幅度大大低于线谱噪声降低的幅度。至于对总体噪声的影响,因为得不到2种噪声的绝对强度值,因此无法进行比较。

?
2.2 叶片数与噪声水平的关系
第2.1节分别说明了线谱噪声和宽带噪声的比较方法,以下各节将不再重复,直接给出结果。
为研究叶片数对噪声水平的影响,设计了4个对比方案,这4个方案的水动力性能相同,导管也相同,只是转子与定子的叶片数不同。叶片各断面的叶形也基本相同,只是在改变叶片数以后,为保持水动力性能不变,对叶片作了少许调整。表2是不同叶片数方案计算结果的相对比较。
从表2的数据可见,叶片数和侧斜值的影响是一致的,即线谱噪声随叶片数的增加而降低,但宽带噪声随叶片数的增加而升高。不过宽带噪声增加的幅度比线谱噪声降度的幅度要小得多。而且叶片数对线谱噪声的影响非常大,其程度已大大超过了后者。
这里需要说明的是,表2中2~4号方案径向力的计算结果的可靠性不高(表现在时域波形曲线不规则,含有明显的随机成分)。出现这个现象的原因是径向力本身的数值已经很小,所以数值误差所占比重就大大增加了。笔者认为,表2中径向力的数值本身并不可信,但径向力随叶片数增加而大幅度降低则是肯定的。数据还说明,无论是转子还是定子,增加叶片数都可降低线谱噪声水平。
2.3 转速与噪声水平的关系
为探究推进器的转速对噪声的影响,采用第2.2节中的第1个方案,将转速降低25%,直径放大到1.179倍,使得在设计航速下,二者的推力相同。表3是计算结果比较。

?
可见,转速降低以后,线谱噪声水平增加,但宽带噪声水平降低。按照Proudman模型,宽带噪声降低的幅度还不算太小。
2.4 定子与转子之间的距离对噪声水平的影响
仍然以第2.2节中方案1为基准,分别将定子与转子叶片盘面之间的距离增加到1.25和1.5倍,为容纳转子和定子叶片,导管长度也相应增加,但叶片形状与大小保持不变。计算所得的结果如表4所示。

?
由表4的数据可见,距离对线谱噪声水平的影响相当大,随着距离增加,线谱噪声水平降低。不同距离的推进器的宽带噪声的数值差别很小,基本上在误差范围以内,可忽略不计。
2.5 其他因素的影响
除以上4种几何参数外,还对转子叶端间隙以及推进器和尾翼之间的距离进行了比较研究,但结果表明这2个因素影响很小,故本文未予讨论。
3 结语
本文采用作用于推进器的径向力的脉动幅值来衡量线谱噪声水平,采用Proudman提出的声功率和Lilley提出的AALS两个参数来衡量推进器的宽带噪声水平,并从理论上说明了采用这3个参数的根据。
运用上述指标对不同几何参数的推进器设计方案的噪声水平进行了比较,发现推进器几何参数与噪声水平之间存在明确的关系和规律。这些规律可以成为进行低噪声推进器水动力设计的指导方针。
对于线谱噪声水平影响最大的因素是叶片数,其次是叶片的侧斜程度以及定子与转子叶片之间的距离。在一定的总推力条件下,增加转速减小直径也可以降低线谱噪声,但幅度不大。
上述因素对宽带噪声的影响正好相反,除了定子与转子之间的距离对宽带噪声没有影响以外,凡是降低线谱噪声的措施都会增大宽带噪声。不过除了转速以外,其他因素对宽带噪声的影响并不大。
降低宽带噪声的主要手段是降低转速。这虽然使得线谱噪声有所增加,但所增加值与通过其他措施降低的幅度相比,应当是相当小的。
[1]巴温 B.螺旋桨现代计算方法[M].北京:人民交通出版社,1986.
[2]张永坤,熊鹰.螺旋桨无空泡噪声预报[J].噪声与振动控制,2008,(1):44 -47.
[3]赵小龙.螺旋桨辐射噪声预报方法研究[D].武汉:海军工程大学,2005.
[4]孙红星,朱锡清.螺旋桨离散谱频噪声计算研究[J].船舶力学,2003,(8):105 -109.
[5]CARLEY M.The sound field of a rotor in a stationary duct[J].Journal of sound and Vibration,2003,259(5):1067-1079.
[6]Fluent用户手册[M].
[7]Star-CD用户手册[M].
[8]KARWEIT M.et al.Simulation of the propagation of an acoustic wave through a turbulent velocity field:A study of phase variance[J].Journal of the Acoustical Society of America,1991,89(1):52 -62.
