电压稳定和同步稳定的关联性研究
2011-08-18翟小勃蒙小明
翟小勃 蒙小明
(1.青海西部水电有限公司,西宁 810000;2.陕西地方电力(集团)有限公司洋县供电分公司,陕西 洋县 723300)
1 引言
在超高压大电网中最常见的稳定性事故,仍然首推功角稳定性的破坏,鉴于此,同步稳定一直是电网公司首要关注的对象。近些年来,在环境的压力、能源短缺的限制以及经济利益的驱使之下,系统的运行越来越接近极限状态,电压稳定现象不断发生。国际上一些大电网相继发生的多起以电压崩溃为特征的电网瓦解事故在很大程度上促进了国际电工学界对电压稳定的研究兴趣,电压稳定和同步稳定成为电力系统稳定运行的最主要方面。众所周知,单机单负荷系统只有电压稳定问题,单机无穷大系统只有同步稳定问题。但系统不可能运行在这种极限情况,因此电压稳定和同步稳定可能会同时存在。文献[1]简要分析了电压稳定和同步稳定的关系,但是针对的是无损网络。文献[2]基于恒功率负荷,简要分析了负荷位置、负荷功率因数、发电机和网络功率流向对电压稳定和同步稳定关联性的影响。本文采用一个典型的系统,基于小扰动分析方法,分析了不同静态负荷模型下的鞍结分叉点和极限功率点的关系和电压稳定与同步稳定的关系,得出了一些有意义的结论,具有一定的理论意义和实际意义。
2 电压稳定和同步稳定关联性的小干扰分析方法
电力系统本质上是一个高维数非线性系统。从数学的角度看,电力系统的动态行为可以用微分代数方程组的形式来描述:

式中,x为系统微分状态变量;y为系统代数状态变量;μ为系统控制参数。
当系统受到小扰动时,可以用线性化系统的动态稳定性来近似,在平衡点(x0,y0,0μ)处对(1)式进行线性化:
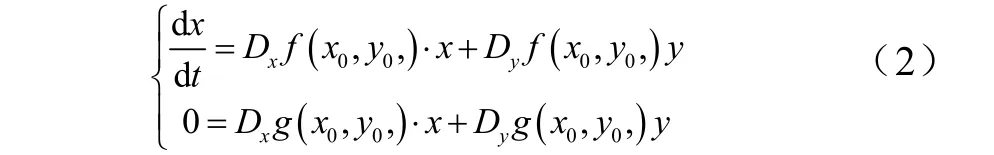
令A11=Dxf( x0, y0,);A12= Dyf( x0, y0,);A21=Dxg( x0, y0,);A22=Dyg( x0,y0,),则系统拓展雅克比矩阵A、发电机矩阵Ag、负荷矩阵 Al分别为
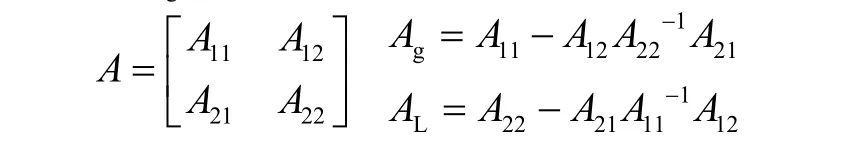
在仅考虑发电机动态时,发电机矩阵Ag常被用来判断同步稳定性[3]。小扰动分析方法通过判断矩阵A、Ag、 Al的奇异性变化来研究电压稳定和同步稳定的关系,即如果 Al比Ag更接近奇异,则认为系统由电压稳定性主导;反之,则认为系统由同步稳定性占主导。
3 系统模型及其参数
等值电力系统如图1所示,负荷由无穷大系统和一等值发电机供电[3]。系统参数如表1所示。
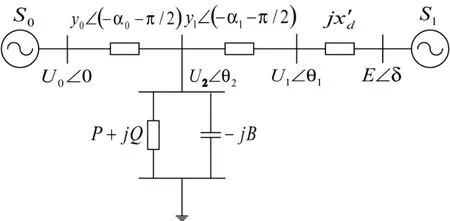
图1 等值电力系统
图中,y0、y1为输电线路导纳;B为负荷无功补偿电纳;P、Q为负荷吸收的有功、无功功率;E为发电机电势。
发电机采用经典二阶模型,由下列方程描述

式中,M为发电机惯量;D为发电机阻尼系数;Tm为发电机机械功率。
静态负荷模型反映了负荷有功和无功功率随电压缓慢变化的规律,经典指数负荷模型的代数方程式描述为
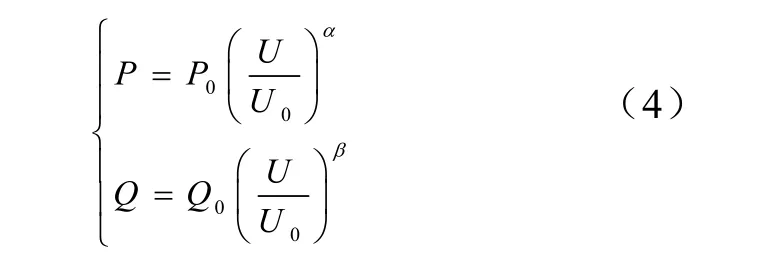
式中,P0、Q0、U0为稳态时负荷吸收的有功、无功功率以及母线电压幅值;α、β为负荷有功、无功功率电压特性指数。
上述方程加上网络代数方程便组成了可用于小干扰分析的微分代数方程组。系统的具体参数如表1所示。
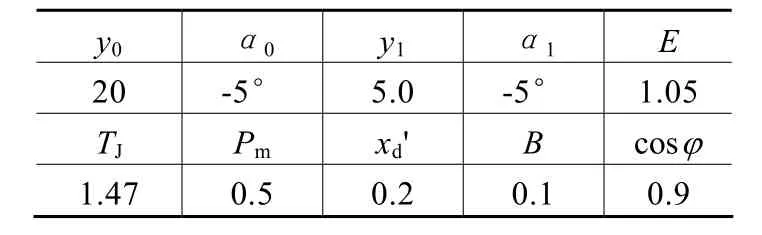
表1 系统参数表
4 仿真分析
采用上面的模型及其参数,分析恒定功率(α=β=0)、恒电流(α=β=1)以及恒阻抗(α=β=2)负荷模型下电压稳定与同步稳定的关联性。
4.1 不同负荷模型下的P-V曲线分析
不同负荷模型下对应的P-V曲线以及搜索到的鞍结分叉点分别如图2、表2所示。可以看出,不同负荷模型对应的P-V曲线完全相同。采用恒功率负荷模型时,P-V曲线上存在三个鞍结分叉点(NB1、NB2、NB3),且极限功率点是其中一个鞍结分叉点;在恒电流和恒阻抗负荷模型下,P-V曲线上都只有一个鞍结分叉点(分别为NB5、NB4),且与极限功率点不重合。
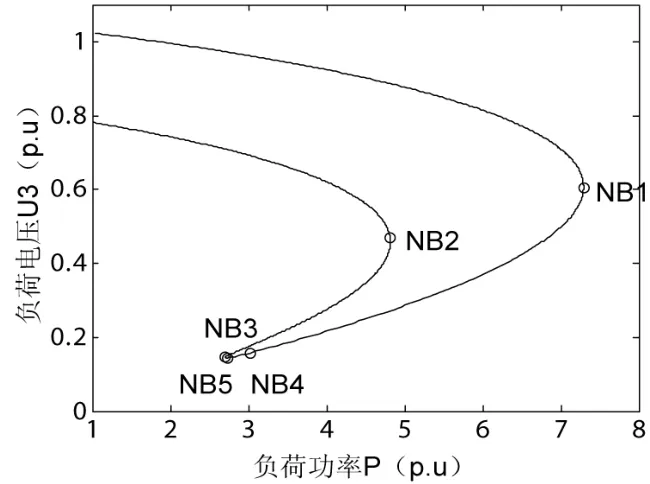
图2 不同负荷模型下的P-V曲线与分叉点

表2 P-V曲线上的分叉点
4.2 不同负荷模型下的平衡点及最小模特征值分析
(1)在恒功率负荷模型下,可变参数就是负荷功率,因此系统的平衡解流形就是上面的P-V曲线。鞍结分叉点NB1之前、NB2-NB3区段的系统矩阵、发电机矩阵以及负荷矩阵最小模特征值变化如图3、图4所示。
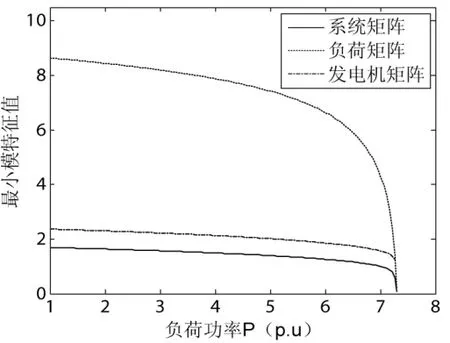
图3 NB1之前最小模特征值变化曲线
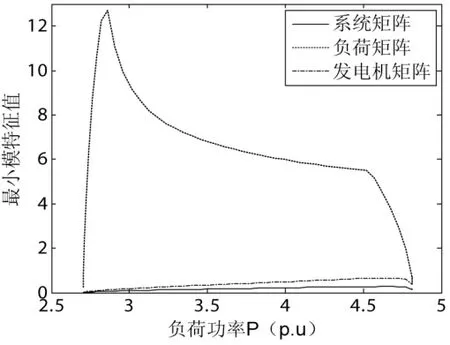
图4 NB2-NB3段特征值变化曲线
从图中可以清楚的看出,系统最开始只有两个平衡点,在NB3点系统分叉出两个个平衡点,此时系统有四个平衡点;随着功率的增加,其中的两个平衡点不断接近,最终在 NB2点因为鞍结分叉的发生而消失;随后,剩余的两个平衡点也不断相向运动,当功率达到一定程度时,发生鞍结分叉,平衡点融合消失。从图3、图4可以看出,在NB1附近,负荷矩阵比发电机矩阵更接近奇异,因此NB1点是电压主导鞍结分叉点;在NB2、NB3附近,发电机矩阵比负荷矩阵更接近奇异,也就是说NB2、NB3点为功角主导鞍结分叉点。可见,当负荷为恒功率模型时,系统完全可能同时存在电压稳定和同步稳定问题。
(2)恒电流负荷时,可变参数为负荷电流。系统的平衡解流形以及鞍结分叉点 NB4之前发电机矩阵以及负荷矩阵最小模特征值变化如图5、图6所示。
可以看出,系统一直有两个平衡点。随着可变参数的增加,这两个平衡点最终在鞍结分叉点NB5处融合消失。在NB4点,系统矩阵、发电机矩阵以及负荷矩阵同时趋向奇异,即系统同时存在电压稳定和同步稳定问题。
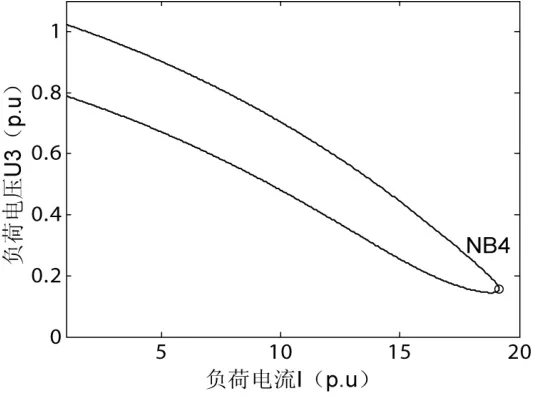
图5 负荷I-U曲线
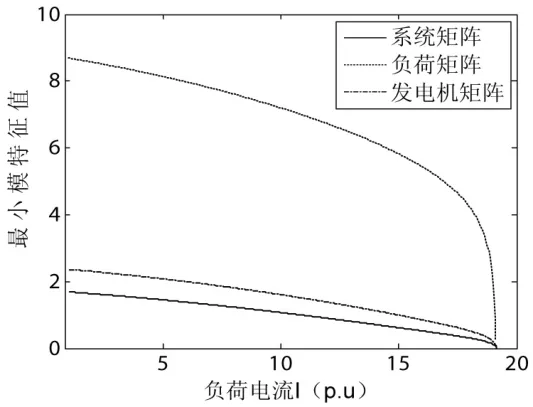
图6 NB4之前最小模特征值变化曲线
(3)在横阻抗负荷模型下,可变参数为负荷导纳。系统的平衡解流形以及鞍结分叉点NB4之前发电机矩阵以及负荷矩阵最小模特征值变化如图 7、图8所示。
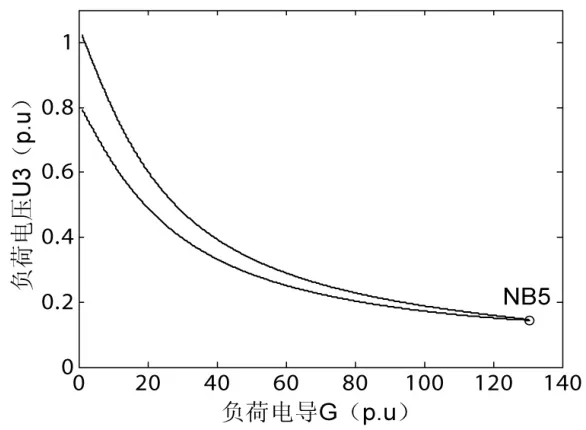
图7 负荷G-U曲线

图8 NB4之前最小模特征值变化曲线
从图可以推知,类似于恒电流负荷模型情况,系统一直存在两个平衡点。由于恒阻抗负荷不存在电压稳定性问题,因此该鞍结分叉点由同步稳定问题导致,从图8也可以看出这一点。
5 结论
从上面的数值计算结果可以看出,在恒功率、恒电流以及恒阻抗三种负荷模型下,系统具有相同的P-V曲线形状。所不同的是,在恒功率负荷模型下,有三个鞍结分叉点存在并且极限功率与其中一个分叉点处的计算值相同;而在恒电流以及恒阻抗负荷模型下,只有一个分叉点存在,且极限功率不等于分叉点的计算值。
从系统稳定角度来看,恒功率负荷模型下的平衡解流形比较复杂,系统的平衡点个数因为分叉的发生变化复杂,电压稳定和同步稳定可能会同时存在。而恒电流和恒阻抗负荷模型下的平衡解流形相对简单,在鞍结分叉发生之前,系统都只有两个平衡点存在。
[1]吴浩.电力系统电压稳定研究.浙江大学博士论文.
[2]彭志伟,胡国根,韩帧祥.基于分叉理论的电力系统电压稳定研究[M].北京:中国电力出版社,2005.
[3]P.W.Sauer, M.A.Pai. Power system steady-state stability and the load-flow Jacobeans [J].IEEE Trans on Power System,1990,5(4):1374-1383
[4]Thierry Van Cutsem, Costas Vournas.Voltage stability of Power systems[M].北京:中国电力出版社,2008.3
[5]V.Venkatasubramanian, H.Schaettler, J.Zaborszky.Voltage Dynamics: Study of a Generator with Voltage Control,Transmission, And Matched MW Load [J].IEEE Transaction on Automatic Control, Vol.37, No.11,November 1992:1717-1733.
[6]C.Guoyun, D.J.Hill, R.Hui. Continuation of Local bifurcations for Power System Differential Algebraic Equation Stability Model [J].IEE Proc.-Gener. Transm.Distrib.Vol.152, No.4, July 2005
[7]IEEE Committee Report. Excitation System Model for Power System Stability Studies.IEEE Trans on Power Apparatus System.Vol.PAS-100,No.2,Feb.1981: 494-509.
[8]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
[9]IEEE Committee Report. Excitation System Model for Power System Stability Studies.IEEE Trans on Power Apparatus System. Vol.PAS-100, No.2, Feb.1981:P494-509.
[10]Carson W. Taylor. Power System Voltage Stability.McGraw-Hill, Inc.1994.
