基于复杂网络理论的典型电力电子电路复杂性研究
2011-08-13魏民,王莉,张强
魏 民,王 莉,张 强
(空军工程大学 导弹学院,陕西 三原 713800)
电力电子电路系统具有严重的非线性,其元件过载能力小,易于损坏。为了减少损失,预防和诊断电力电子电路就显得尤为重要。因此,需要对电力电子电路的结构特性进行研究,以保证电力电子电路的安全稳定运行。应用复杂网络系统理论的成果研究系统的复杂性问题正越来越受到学术界的关注[1-3]。
从20世纪70、80年代开始,复杂性问题的研究与非线性科学及其混沌动力学的复杂研究交错在一起,在国际上形成了非线性科学与复杂性问题的研究热潮[4]。而利用复杂网络理论来研究非线性复杂网络的方法已渗透到众多学科之中。将电力电子电路系统看成一个网络,可以用复杂网络特性的统计指标描述电力电子电路系统整体的状态,从而研究电力电子电路系统复杂网络的特性。复杂网络为其提供了一个全新的视角和研究方法[5],从复杂网络的角度来分析和研究电力电子电路系统,有助于从整体上把握它的复杂性。
三相全控整流电路的整流负载容量较大,输出电流电压脉动较小,是目前应用最为广泛的整流电路,逆变电路在电力电子电路中占有十分突出的位置,其应用非常广泛,在三相逆变电路中,应用最广泛的应是三相电压型桥式逆变电路。本文以三相桥式全控整流电路及三相电压型桥式逆变电路为例将复杂网络应用到电力电子电路系统,用复杂网络的原理对电力电子电路的复杂性进行了分析[6-7]。
1 复杂网络的几何量
用图的顶点(或称为节点)代表所研究的事物,用图的边表达事物之间的联系,这样能较好地刻画出所研究的系统。在复杂网络中,人们最先考虑的是其统计特征:平均路径长度、聚类系数和度的分布律。具有较短的平均路径长度、较高的聚类系数是小世界网络[8]的典型特征,网络的度分布服从幂律分布时被称为无标度网络[9]。
如果把电力电子电路系统看作许多元件和各个电路的集合,把元件称为 “节点”,并且把电路都称为“边”,则电力电子电路系统就被抽象、简化为一张普通意义上的“复杂网络”。复杂网络的基本几何量有:最短路径、平均距离、聚类系数、节点平均度数及节点度数分布、节点的介数及节点的介数分布等特征参数的规律。其定义分别如下:
(1)最短路径Lij。两点的最短路径Lij定义为所有连通i,j的通路中,所经过的其他顶点最少的一条或几条路径。
(2)平均距离L。网络中两个节点i,j之间的距离dij定义为连接这两个节点的最短路径上的边数。对任意两个节点之间的距离求平均值,就得到了该网络的平均距离:

其中N为网络节点数,平均距离反映了网络中节点之间信息传播的平均长度。
(3)聚类系数C。网络的聚类系数C是专门用来衡量网络节点集聚程度的一个重要参数。每个节点的聚类系数可表示为:

式中,ai为连接到顶点i的三角形的个数;bi为连接到顶点i的三元组的个数。整个网络的聚类系数定义为:

(4)网络平均度数K。节点的度数是指连接这个节点的边数。对所有节点的度数求平均值,即得到网络的平均度数K。对于一个边数为E、节点数为n的网络,其平均度数可表示为:

(5)节点度数分布 Pcum(k)。 用 p(k′)表示度数为 k′的节点个数占节点总数的百分比,则节点度数的积累概率为:

(6)节点介数分布Pcum(s)。节点介数是指所有最短路径中必须经过此节点的次数。用p(s′)表示介数为s′的节点个数占节点总数的百分比,则节点介数的累计概率为:

2 典型电力电子电路网络特性分析
2.1 三相桥式全控整流电路特性分析
三相桥式全控整流电路原理图如图1所示。如果把该图系统看作许多元件和电路的集合,把元件称为“节点”,并且把电路称为“边”,该整流电路系统就被简化为一张“复杂网络”,如图2所示。
本文将上一节的算法编制成MATLAB程序,通过式(1)~式(6)计算上述基本参数,并对三相桥式全控整流电路的网络特性以及其他相关的重要拓扑特性进行分析。其中将三相桥式全控整流电路网络简称为A网络。其拓扑参数如表1所示。其中,K表示网络平均度;L表示网络平均路径长度;C表示网络聚类系数。
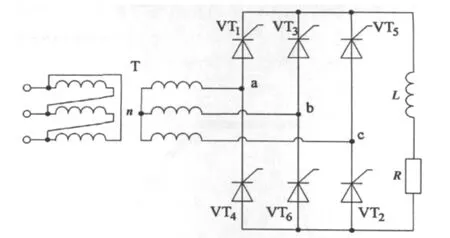
图1 三相桥式全控整流电路原理图
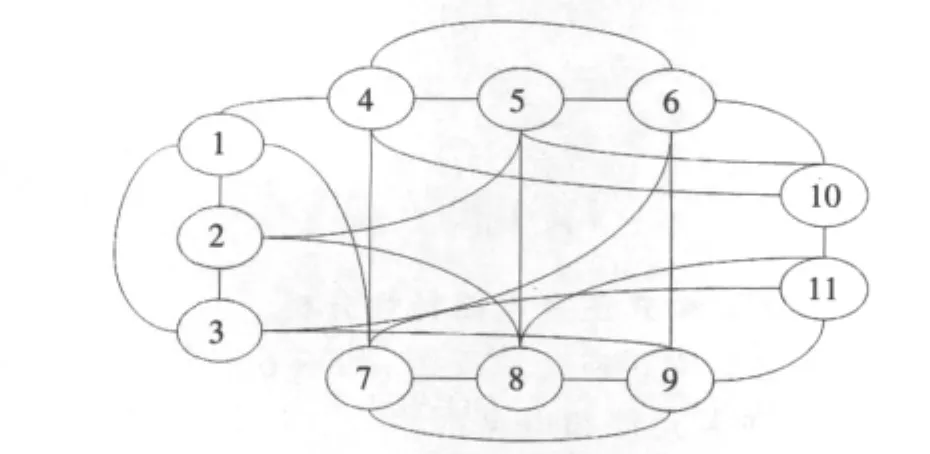
图2 三相桥式全控整流电路网络示意图
由表1及图3可知,从网络拓扑参数方面考虑,A网络由于网络规模较小,平均路径较短,所以故障传播速度比较快,且对照图1、图2可以看出度数较大的元件为与三相电源相接的晶闸管。图4说明A网络的度分布在对数坐标系中对应于一条直线,符合幂律分布。

图3 A网络各节点度大小分布图

表1 A网络拓扑参数
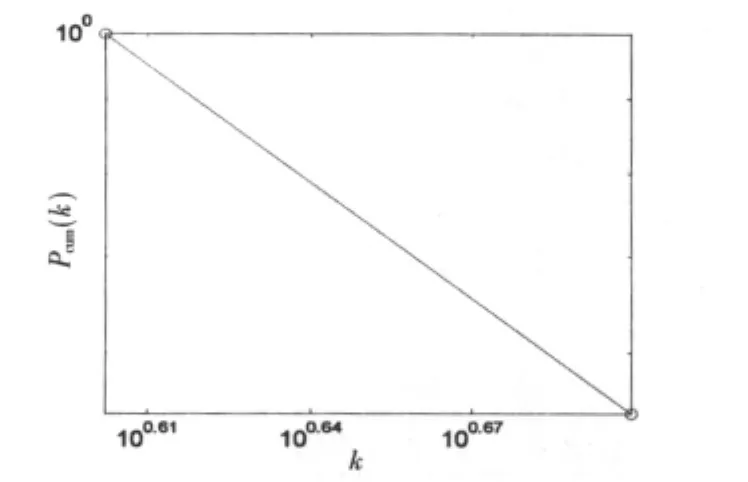
图4 A网络节点度数分布
图5的曲线表明,A网络的介数分布曲线在对数坐标下呈线性,符合幂律分布,而具有幂律度分布的网络也称为无标度分布,所以A网络为无标度网络,具有无标度网络的特性。
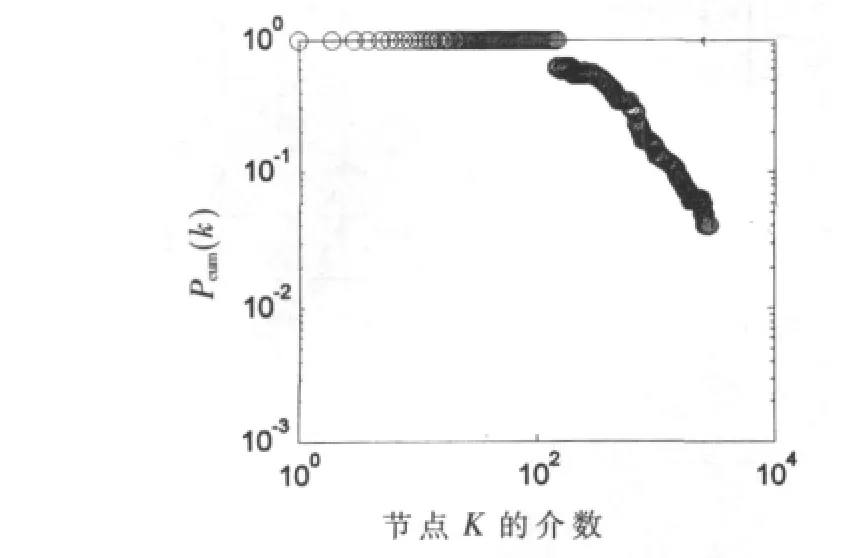
图5 A网络节点介数分布
2.2 三相电压型桥式逆变电路特性分析
三相电压型桥式逆变原理图,如图6所示。如把该图系统看作许多元件和电路的集合,同样把元件称为“节点”,并且把电路称为“边”,该逆变电路系统就被简化为一张“复杂网络”。如图7所示,将三相电压型桥式逆变电路网络简称为B网络。其拓扑参数如表2所示。其中,K表示网络平均度;L表示网络平就路径长度;C表示网络聚类系数。
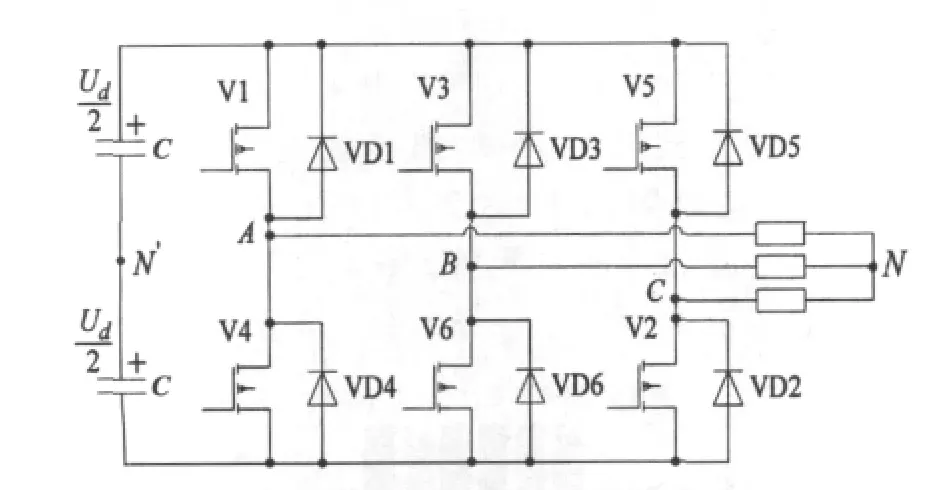
图6 三相电压型桥式逆变电路原理图
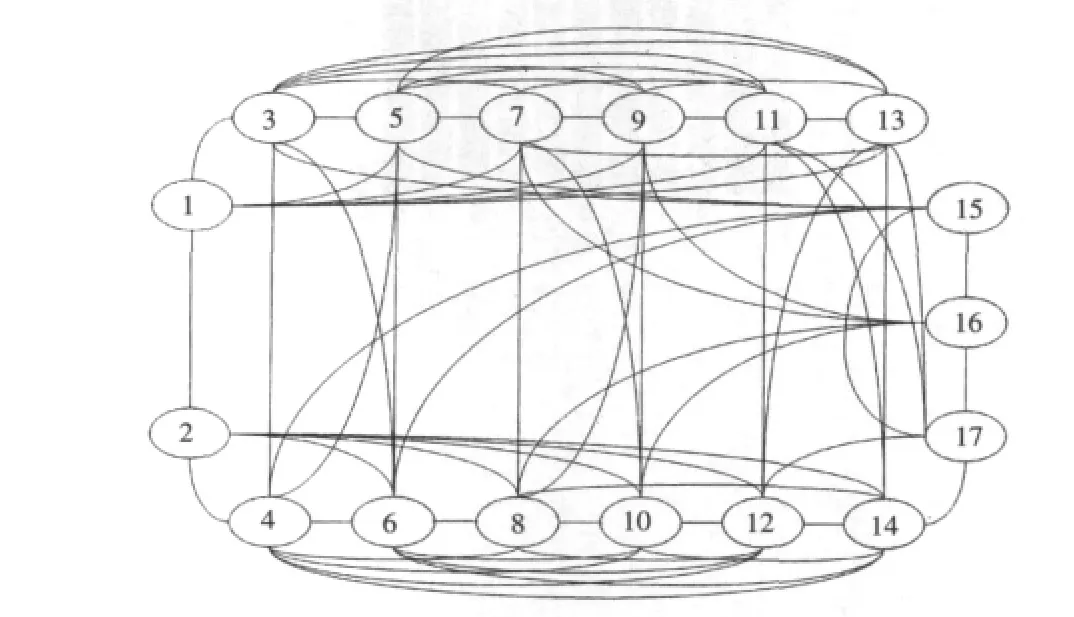
图7 三相电压型桥式逆变电路网络示意图

表2 B网络拓扑参数
由表2及图8可以看出B网络在网络拓扑参数方面平均度比较高,高度数节点相对集中,所以故障传播速度也比较快。对照图6、图7可知其度数较大元件为功率开关器件。图9说明B网络的度分布在对数坐标系中对应于一条直线,符合幂律分布。
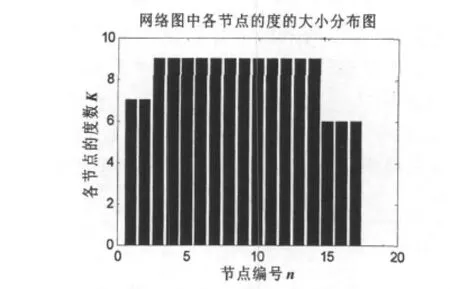
图8 B网络各节点度大小分布图
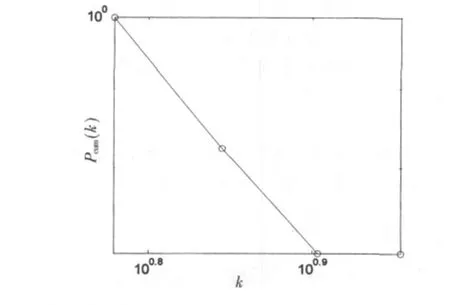
图9 B网络节点度数分布
如图10所示,B网络的介数分布曲线在对数坐标下呈线性,所以B网络同样为无标度网络。

图10 B网络节点介数分布
由上面所述的2个典型电力电子电路系统网络可以看出,电力电子电路系统网络多为无标度网络,其中存在部分度数和介数很高的节点,成为网络的重要支撑点。下面将对这2个网络进行鲁棒性、脆弱性的仿真研究,通过仿真来验证这部分节点对系统产生的重要影响。
3 典型电力电子电路的网络鲁棒性与脆弱性研究
目前,普遍使用的衡量网络特性的指标是效能函数。整个网络G的功效性指标定义如下:
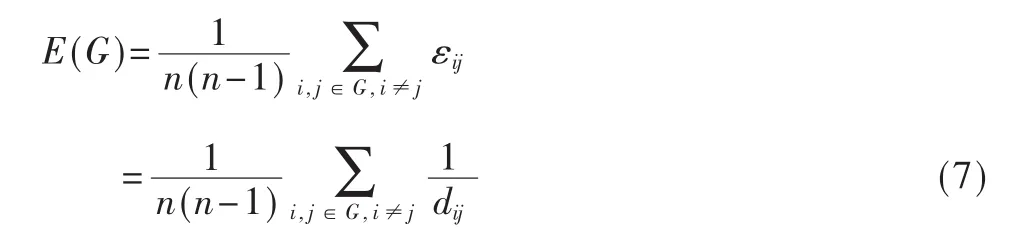
假设εij表示两节点之间的通信效率,与这两节点之间的最短距离成反比,而当dij=∞,即两节点之间没有路径时 εij=0。
攻击脆弱性是复杂网络研究的一个热点分支,其基本定义是从网络中有选择地或有针对性地移去网络元件,以网络性能下降的程度来衡量此元件的脆弱度。而通过随机移除网络元件来考察网络性能的分析过程被称为网络的鲁棒性分析,研究目的在于识别出对系统功能影响严重的故障,从而采取正确的预防、校正措施,实施保护。
经过以上的参数计算,得到节点度数排序和节点介数排序,针对这两种情况,对网络进行攻击仿真,观察网络效能的变化情况,并与随机攻击相对比。攻击联络节点的方式可分为:随机攻击某个节点,并逐步增加被攻击节点的个数;有选择地蓄意攻击度数最大的节点,并依次攻击度数次大的节点;有选择地蓄意攻击介数最大的节点,并依次攻击介数次大的节点。
从仿真结果可以得出,节点的失效使得网络的特性曲线下降。蓄意攻击所引起的网络效能下降比随机攻击造成的影响要大,效能曲线的变化更快。A、B两个网络均为无标度网络,在蓄意攻击的模式下,失去很少的节点就能使得效能下降很快,这说明A、B网络对随机元件故障具有高度的鲁棒性,对蓄意攻击具有高度的脆弱性。网络结构的不平衡性使少数高介数和高度数节点能对网络产生很大的影响,对于这种小型电力电子网络来说,连接度比较高的节点和传输次数比较多的路径的点造成了这种结构上的不平衡,成为了网络上的脆弱点。综上所述,可以将介数和度数指标作为衡量网络脆弱点的标准,对小型电力电子网络来说,故障是不可避免的。通过上述分析可知,三相桥式全控整流电路的晶闸管和三相电压型桥式逆变电路的功率开关器件为上述的脆弱点,且实际运行表明其元件损坏确实为绝大多数故障的原因。因此,必须加强与网络结构相关联的节点的保护,保证结构更加平衡来提升性能。
可以看出,电力电子电路中多为无标度网络,其网络的非均匀性使得对蓄意攻击具有高度的脆弱性。
通过对典型电力电子电路鲁棒性与脆弱性的研究,发现了电力电子电路系统潜在的脆弱点,分析了影响网络脆弱性的因素。今后的研究将围绕系统元件的承受能力限制来进行研究,使这种分析方法更加完善。
[1]DOBSON I,CARRERS B A,LYNCH V E,et al.Complex systems analysis of series of blackouts,cascading failure,criticality,and self-organization[C].//9thBulk Power System Dynamics and Control-VI Cortina d’Ampezzo,Italy,2004:438-451.
[2]CARRERAS B A,NEWMAN D E,DOBSON L,et al.Evidence for self-organized criticality in a time series of electric power system blackouts[J].IEEE Trans Circuits and System,2004,54(9):1733-1740.
[3]DOBSON I,CARRERAS B A,LYNCH V E,et al.An initial model for complex dynamics in electric power system blackouts[C].//proceedings of 34th Hawaii International conference on system sciences.Maui,Hawaii January,2001,710-718.
[4]方娜清,汪小帆,刘增荣.略论复杂性问题和非线性复杂网络系统的研究[J].科技导报,2004,22(2):9-12,64.
[5]孙可,韩祯祥,曹一家.复杂电网连锁故障模型评述[J].电网技术,2005,29(13):1-9.
[6]欧阳敏,费奇,余明辉.复杂网络的功效性与脆弱性研究综述[J]. 计算机科学,2008,32(7):1-4.
[7]丁明,韩平平.加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报,2008,28(10):20-25.
[8]WATTS D J,STROGATZ S H.Collective dynamics of‘small worlds’ networks.Nature,1998,393(6884):4404-42.
[9]JEONG,TOMBER H B,ALBERT R,et al.The large scale-organization of metabolic networks.London Nature,407(2000):6516-54.
