基于PTPR排名的基因随机选择算法
2011-08-13解瑞飞厉力华
解瑞飞 韩 斌 厉力华 祝 磊
(杭州电子科技大学生命信息与仪器工程学院,杭州 310018)
引言
高维、小样本数据是生物医学信息处理中经常遇到的数据类型,如何剔除其冗余特征、提高数据质量,成为研究识别和分类问题的关键[1-2]。
近年来,Draminski等结合随机搜索策略[3]和决策树[4],提出 Monte Carlo(MC)特征选择算法[5]。它是一种随机搜索的特征选择算法,降低了结果陷入局部最优的风险,对高维数据具有较强的适应性。同时,最终变量排名综合考虑了分类率及变量的重要性,与经典方法相比,克服了缠绕法(如SVMRFE)依赖分类器的缺点,以及单纯依靠分类率所引起的弊 端[6-7];与 过滤法 ( 如 T-test[8])相 比,MC不需要样本呈正态分布的假设,比T-test更加适合真实的基因微阵列数据;和 SVMRFE[9]相比,MC可以更加快速高效地提取出高维数据中的显著变量。
虽然MC方法比传统方法有更多的优点,但是其在搜索过程中没有规划,在不同的迭代间相互独立并且不相关,没有合理利用历史成绩和当前排名,搜索效率低,结果稳定性差。本研究在MC算法基础上,提出基于职业网球选手排名(professional tennis player ranking,PTPR)的基因随机选择算法。实际上,选手排名和基因选择面临相似的问题,例如,注册的职业选手有几十万人,其中参与PTPR官方网站排名的就有近1500人,但每年认可的赛事大约70场,因此从特征选择角度来看是典型的“维灾”问题,目的是通过大量选手(基因)随机参加赛事(基因比较)来对选手进行排名。此外,两者还有许多类似的地方,见图1。更重要的是,作为权威排名,职业网球选手的排名方法在解决排名问题上有很多可以借鉴的地方:一是通过不同赛事对选手进行综合滚动排名,体现了选手的整体平均水平,而非由一场赛事决定最终的结果;二是考虑保留种子选手(根据以前比赛成绩所选出的高水平选手),把种子选手刻意划分在不同的小组,可以最大限度地避免种子选手过早相遇而被淘汰,同时提高了每场赛事的水平;三是因不同赛事对选手排名的贡献不同,PTPR选手的排名同样也考虑了赛事本身的质量对选手排名的影响。因此,借鉴PTPR的权威排名,笔者提出了基于PTPR排名的随机选择算法(称为“PTPR算法”),该算法保留了 MC算法的精髓,即随机选择,同时借鉴PTPR排名机制,引入了种子变量排名、排名滚动更新,优化了搜索过程,提高了搜索效率,保持了结果稳定。
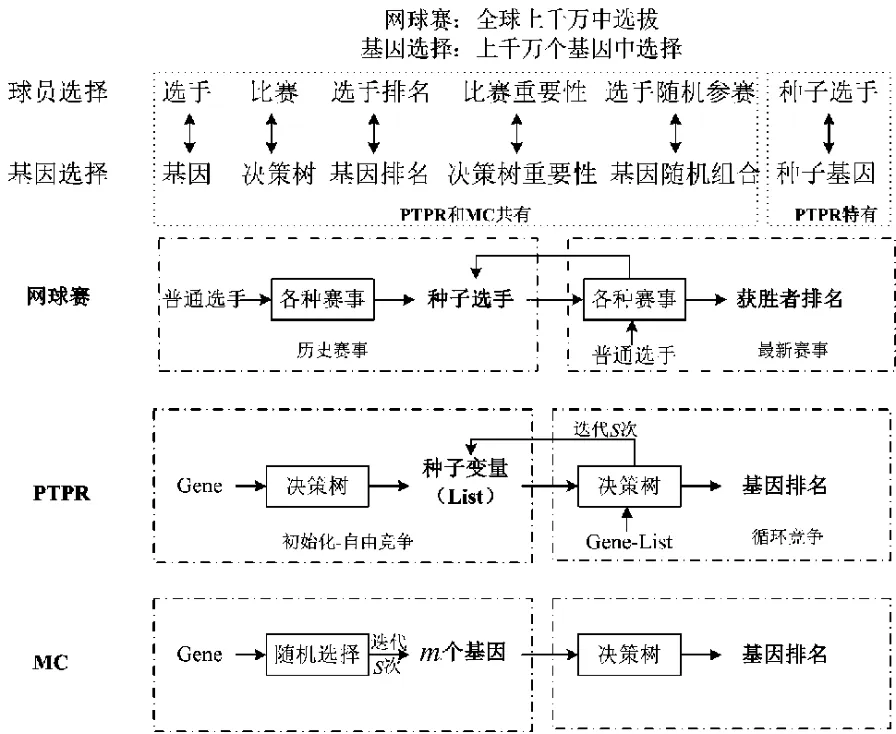
图1 网球比赛和特征选择类比Fig.1 The analogy between tennis competition and feature selection
1 方法
1.1 数据来源
采用的测试数据包括Leukemia[10]、Colon[11]、Glioma[12]、Prostate[13]及 Ovarian 共 5 个基因微阵列数据集。Leukemia、Colon、Prostate和 Glioma基因表达谱数据来自于公共数据库,已被许多研究者进行了分析和研究,Ovarian来自于美国 Duke大学医学中心和美国Moffitt肿瘤研究中心,具体样本见表1。
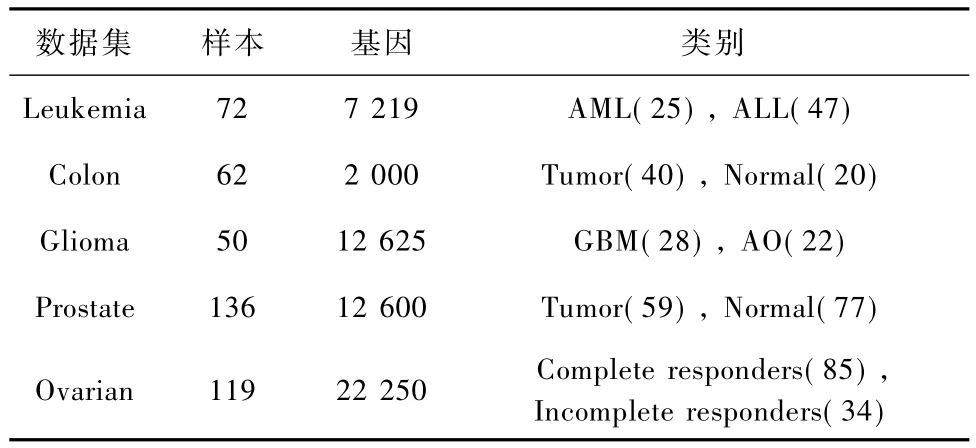
表1 数据集描述Tab.1 The description of data sets
1.2 特征选择方法
基于职业网球选手排名的特征提取方法(PTPR),根据对职业网球选手排名和基因选择问题的分析,笔者把PTPR的思想引入到特征提取方法中,在MC算法的基础上,形成一种新颖的特征选择算法——基于PTPR的特征选择算法,简称PTPR。
1.2.1 特征随机选择方法
特征随机选择(MC)算法通过建立成千上万个决策树,然后计算所有决策树各节点(特征基因)的重要性,以此作为最终衡量基因排名的指标,有
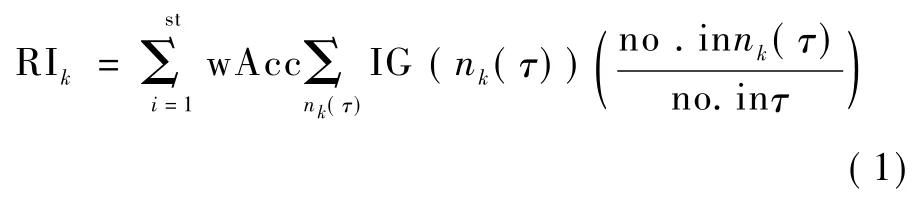
式中,k为决策的结点(特征基因),wAcc为特征基因k所在决策树的分类率,IG(nk(τ))为特征基因k在第树中所在结点 nk(τ)处的信息增益,no.in nk(τ)为结点 nk(τ)处的样本数,no.in τ 为第棵树的根结点的样本数。nk(τ)的信息增益为
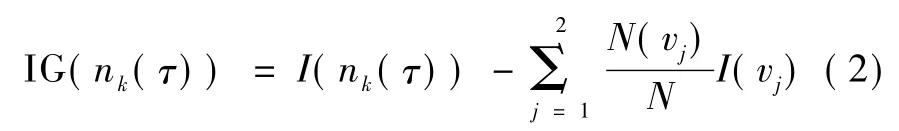
式中,N为结点nk(τ)处的样本数,N(vj)为子结点处的样本数,为子结点出现的概率,I(n(τ))k为结点nk(τ)处的信息熵,可表示为
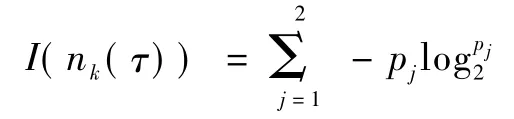
式中,pj为该结点中属于某类的分类概率,I(vj)为子结点处的信息熵。
MC算法在每一次迭代过程中,先随机选择含m个基因的候选集,然后通过决策树比较,累加各变量所对应的 RI值(见式(1))。RI计算基于两点:一是此次决策树的分类率,二是基因在此次比赛中(决策树中)的信息增益和正确分类样本占总样本的比率。待迭代截止后,对所有变量对应的RI进行排名,最终排名是基因随机参加的所有决策树中两项组合(RI)的累计。
1.2.2 基于MC的PTPR算法
在整个迭代过程中,MC算法存在两个问题:第一,基因在不同的比赛间相互独立不相关,中间过程的成绩没有得到合理的利用,搜索效率低;第二,MC算法中的排名是基于选手相对其他所有选手的重要水平(RI),由于选手参与赛事(决策树)的基因完全随机选择。在迭代次数较少时,不同基因参加赛事的次数受随机影响,多少不等,RI受赛事次数影响大,造成结果不公平;在迭代次数足够多时,不同基因参加赛事的次数大致相同,所得到的RI也大致相同,利用RI区分基因不敏感,算法收敛慢。针对MC的问题,PTPR算法模拟了职业网球选手的排名方式,让种子选手和普通选手参加不同等级、水平的赛事,然后根据严格的积分、排名机制,从成千上万个选手中快速高效地筛选出优秀的选手。本研究把网球赛中的“种子选手”思想、滚动排名机制同随机搜索思想结合起来,实现基因的快速提取。网球选手排名和基因排序的类比如图1所示,基因变量相当于选手,种子变量相当于种子选手,决策树相当于各种赛事,而每次参与决策树的基因相当于每次参与赛事的选手。
本研究从搜索策略和排名机制两方面做了改进:首先引入了种子变量,在迭代中,普通变量以固定概率进入赛事(决策树建立),而种子变量以较高的概率进入赛事(因为种子变量的长度远远小于普通变量的长度),保证种子变量参与每一场赛事,提高了赛事的水准,从而提高了比赛的筛选效率。变量排名是List内的种子选手到目前为止的历史成绩比较,同时算法逐次滚动更新当前种子变量排名,保证目前最优秀的选手(基因)参与下一次的比较,进一步提高比赛的筛选效率,有

式中:第一部分是分子RIk,表示基因k到目前为止参与所有赛事成绩的累积,见式(1);第二部分是分母sum(RI.List)/length(List),是当前种子变量的平均历史成绩,其中List用来存放当前的种子变量,length(List)为当前种子变量的个数,RI.List为存放List中种子变量所对应的重要性(每个种子变量的重要性用其 RI来衡量),sum(RI.List)为当前 List中种子变量的重要性总和。
式(3)表示基因k到目前为止其历史成绩与种子变量平均历史成绩的一个比较。需要特别说明的是,相对于MC算法是基于所有选手的获胜记录(RI累计)来排名,PTPR算法的排名则是基于普通选手和种子选手的比较;wRIk是基因参与众多赛事后,相对到目前为止“最优种子选手”平均水平的一个衡量,对基因更具有甄别能力。同时注意的是,分母逐次递增更新,意味着随着迭代逐渐有真正的种子选手进入种子名单,种子名单趋近最优,保证对后面基因的筛选更加公平和高效。通过上面的分析可以看出,PTPR算法最重要的思想是:运用种子变量(滚动更新)及历史信息,标记并保留已搜索到的当前最优变量,并在下一步的迭代搜索中吸纳更优变量,避免因初解不同、盲目搜索对结果造成的动荡不稳定,从而快速高效地筛选出重要基因,其流程图和步骤如图2所示。其中,d为变量候选集,m为变量子集(每次参与决策树比较的变量个数),wRI判决为通过wRI公式计算每个变量的重要性,Seed为存放当前的种子变量,List为存放满足一定条件后的种子变量,d-List为集合d与集合List的差集(即种子变量之外的普通变量),p为概率值,m为变量中来自普通变量的比例。
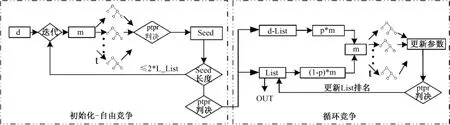
图2 PTPR算法流程Fig.2 The scheme of the PTPR algorithm
PTPR算法由两部分组成,一是自由竞争(或初始化),获得初始的种子变量;二是循环竞争,滚动更新种子变量,得到最终变量排名。两种算法分别包括以下步骤。
1.2.2.1 自由竞争:
步骤1:从d个基因候选集中,随机选择m个基因,构成子集。
步骤2:对于此子集,按照一定比例随机 t次划分训练集和测试集,训练集建立决策树,测试集用来测试所构建的决策树。
步骤3:对步骤2中参与决策树建立的基因,利用wRI公式计算后进行排名,取前X%存入List。
步骤4:判断 List长度。如果小于 n×L_List,重复步骤1;否则,初始化终止。利用 wRI,对 Seed中的基因进行排名。
1.2.2.2 循环竞争
步骤1:判断 List长度,删除 List中 L_List之后的基因变量,得到List补集d-List。
步骤2:从集合d-List中随机选择 p×m个基因(0<p<1),从集合 List中随机选择(1-p)×m个基因,组合为含有m个变量的子集;因d-List长度远远大于List长度,故List中的种子变量以高概率进入决策树,d-List中的普通变量以低概率进入决策树。
步骤3:对于此子集,按照一定比例随机 t次划分训练集和测试集,训练集建立决策树,测试集用来测试所构建的决策树。
步骤4:将步骤3中参与决策树建立的基因加入到 List,在利用 wRI公式计算后,更新List排名。
步骤5:重复步骤1~步骤4至 s次,最后得到List排名。
1.3 PTPR算法验证实验设计原则
衡量一个特征提取算法是否能够提取出有效的特征基因,可以从基因分类率和稳定性两个方面对算法做比较和评估。
1.3.1 基因稳定性及显著差异分析
MC算法和PTPR算法最终得到的都是基因重要性的相对排名,通过观察基因排名随迭代次数的变化规律,可以反映算法的收敛速度,显示最终是否收敛达到稳定性的结果。基因排名变化为
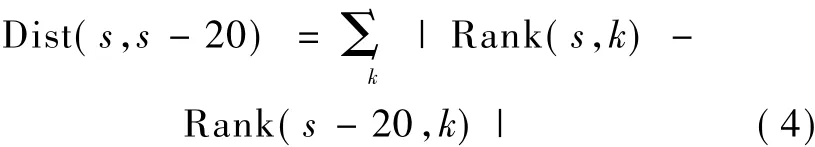
式中,s为迭代次数,k为第 k个基因,Rank(s,k)为基因k的排名位置,(s,s-20)为当迭代次数由 s-20变化到s时基因的相对排名变化量。随着迭代次数s的连续增大,基因排名的变化越来越小,最终趋于稳定。
在特征提取的过程中,从训练集中提取特征,测试集进行分类率的计算,一般需重复多次。即使在其他条件完全相同的情况下(比如特征提取算法、参数及样本比例分配等),训练集具体样本不同造成了所提取的特征基因不同。因此,在不同的训练集上,提取稳定的特征基因成为特征提取算法的一项重要指标。为了验证PTPR算法所提取基因的稳定性,实验包括下列步骤。
步骤1:特征基因获取。随机生成M组训练集,利用MC算法和 PTPR算法,分别提取 M组特征基因。
步骤2:基因重复率定义。对于 PTPR(或 MC)算法所得到的M组特征基因,两两比较,得到前N(N=10,20)个基因的基因重复率,共组,分别为PPTPRN和 PMCN。其中,PPTPRN=[p1,p2,…,pC2M],PMCN=[q1,q2,…,qC2M]。
步骤3:平均基因重复率。计算前N个基因的平均重复率PPTPRN和PMCN(N=10,20),有
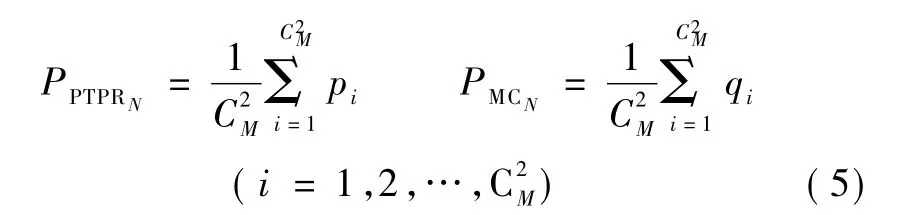
步骤4:基因重复率的显著性分析。在生物信息学研究中,由于所用数据含有较少样本,往往无法满足经典的参数检验条件,可以考虑采用Permutation test进行统计推断。为了验证PTPR算法在基因重复率上是否显著优于MC算法,笔者利用PPTPRN和PMCN数据,根据Permutation原理(由于篇幅限制,原理见附录),计算 P-value,分析基因重复率的显著性差异。
1.3.2 分类率比较
为了验证MC算法和PTPR算法所提取出的特征基因有效性,可以通过比较来挑出基因的分类能力。为了方便比较,数据划分采用通用的划分原则,即Leukemia数据集随机选择38个样本作为训练集,其余34个样本作为测试集[10];Colon数据集,随机选择33%的样本作为测试集,其余样本作为训练集[14];Glioma和 Prostate数据按照 9∶1随机划分训练集和测试集[15];Ovarian数据按照 7∶3,随机划分训练集和测试集。5个数据分别迭代10次,利用常用分类器支持向量机(support vector machine,SVM)、k 最近邻(k-Nearest Neighbor,KNN,K=1)、Naäve Bayes(NB)和 Random Forests(RF),对测试集进行分类比较。
2 结果和讨论
2.1 基因稳定性分析
图3~图7表示不同数据库基因排名 Dist(s,s-20)和基因平均重复率(见式(5))随迭代次数s的变化。PTPR和MC都是随机搜索算法,靠多次的迭代而获得最终相对稳定的最优解。随着迭代次数的增加,基因排名变化幅度的大小体现了算法搜索的稳定性。前后两次迭代所引起基因排名变化越小,说明搜索过程越稳定,从而体现出随机算法稳定性越强。从图3~图7中的(a)可以看出,在5个数据库上,随着迭代次数增加,PTPR算法所得到的基因排名变化幅度小于MC算法所得到的基因排名变化幅度,并快速收敛到比MC更加稳定的水平;而且,PTPR算法在迭代次数较少的时候,基因排名的变化量远远小于 MC算法,体现了PTPR算法相对于MC算法,基因更早地进入到收敛过程中。此外,MC和PTPR算法的计算量基本上是由迭代次数决定的,当特征基因的排名趋于稳定水平时,迭代终止。从图3~图7中可以看出,PTPR以较小的迭代次数,得到了和MC一样的稳定水平,说明PTPR算法比MC计算速度更快、计算量更小。
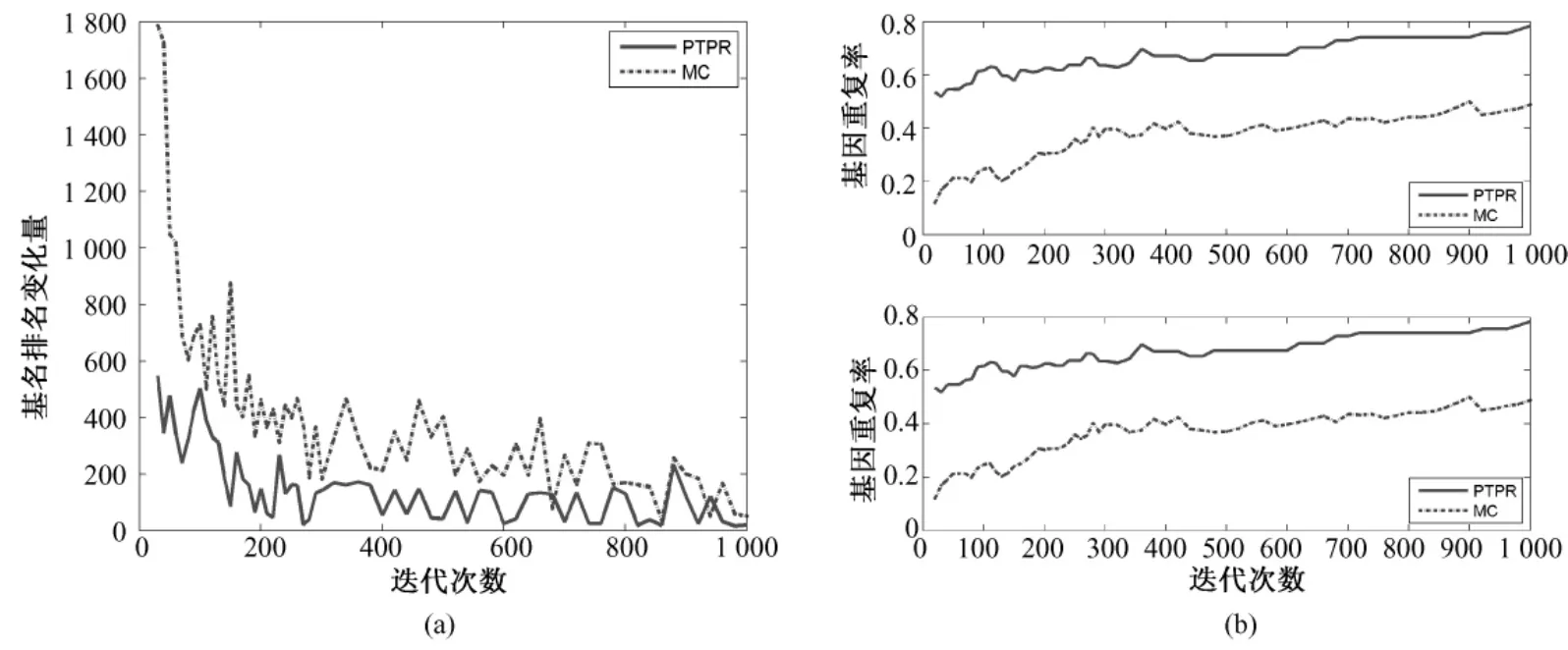
图3 Leukemia—基因稳定性。(a)基因排名的收敛性;(b)前10和前20个基因的重复率(从上至下)Fig.3 Gene stability for Leukemia.(a)convergence of gene ranking;(b)top 10 and 20 genes overlapping rate(from upper to bottom)
对于PTPR和MC等随机算法,因随机因素的存在,即使在其他条件完全相同的情况下,不同时刻的使用所得到的结果也不尽相同。因此,提取稳定的特征基因成为衡量随机算法的一项重要指标。在图3~图7的(b)中,都是由两幅子图组成,分别表示基因个数为10和20的基因重复率,是两种算法分别重复10次所得。在不同的数据集上,PTPR所得到的基因重复率大致介于60% ~80%之间,而MC最高只达到40%左右,即PTPR的基因重复率远远高于MC的结果。具体来说,对于含有w个变量的数据集,利用PTPR所提取出的10组特征基因中,每两组的前10或20等(w≫100)个基因,60%~80%是相同,而MC最高只有40%相同的基因。因此,PTPR能够从成千上万个基因中多次提取出60%~80%相同的基因,在稳定性上比MC算法有显著性的提高。除此之外,从图3~图7中也可以看出,随着迭代次数的增加,虽然两种方法的基因重复率都呈上升趋势,但是MC算法仍然没有超越PTPR算法。

图4 Colon—基因稳定性。(a)基因排名的收敛性;(b)前10和前20个基因的重复率(从上至下)Fig.4 Gene stability for Colon.(a)convergence of gene ranking;(b)top 10 and 20 genes overlapping rate(from upper to bottom)
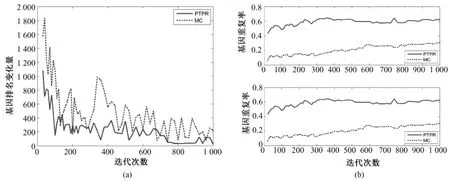
图5 Glioma—基因稳定性。(a)基因排名的收敛性;(b)前10和前20个基因的重复率(从上至下)Fig.5 Gene stability for Glioma.(a)convergence of gene ranking;(b)top 10 and 20 genes overlapping rate(from upper to bottom)
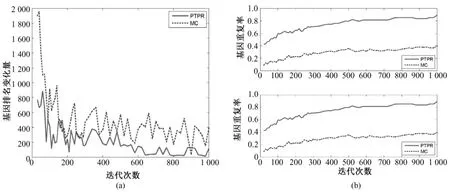
图6 Prostate—基因稳定性。(a)基因排名的收敛性;(b)前10和前20个基因的重复率(从上至下)Fig.6 Gene stability for Prostate.(a)convergence of gene ranking;(b)top 10 and 20 genes overlapping rate(from upper to bottom)
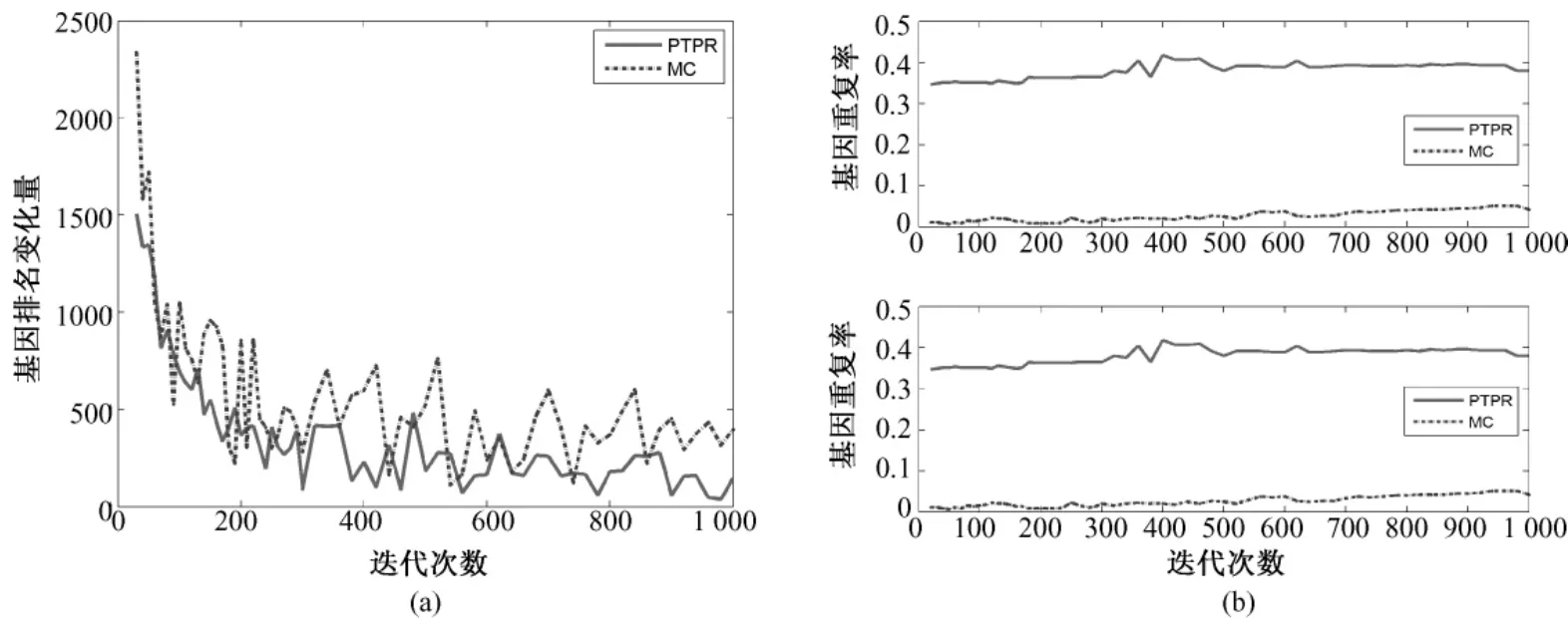
图7 Ovarian—基因稳定性。(a)基因排名的收敛性;(b)前10和前20个基因的重复率(从上至下)Fig.7 Gene stability for Ovarian.(a)convergence of gene ranking;(b)top 10 and 20 genes overlapping rate(from upper to bottom)
对于图3~图7中的(b),为了进一步验证PTPR的基因重复率在统计学角度是否显著高于MC算法,笔者进行了相应的permutation实验,具体的原理见附录。从基因重复率的permutation实验的结果看,在5个数据集上,在迭代次数 s从20变化到1000的过程中,P-value的最高值达到0.0055左右,远远小于 0.05,而大多数的 P-value值为 0。因此,从统计学角度上证明了PTPR算法的基因重复率显著高于MC算法。
2.2 分类率比较
图8~图12中的横坐标都是迭代次数s,纵坐标表示分类率,是5个数据集在不同分类器上的结果;各图中的(a)和(b)分别表示在基因个数为10和20上所得到的分类率,而每幅图又由4幅子图组成,表示在不同分类器 NB、SVM、KNN和 RF(从左至右,从上到下)上所得到的分类率。
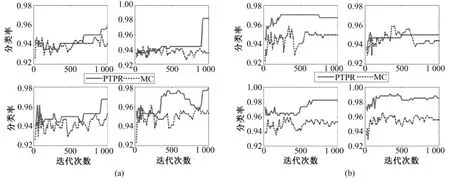
图8 不同基因在NB、SVM、KNN和RF上(从左至右,从上到下)的Leukemia分类率。(a)10个基因;(b)20个基因Fig.8 The classification rate of different gene number in NB,SVM,KNN and RF(from left to right,from upper to bottom)for Leukemia.(a)10 genes,(b)top 20 genes
从图 8~图 12中可以看出,对于 Colon和Glioma数据集,在分类器KNN上,PTPR和MC算法所得的分类率不相上下。但是,在其他数据集和分类器上,PTPR算法所得分类率明显高于MC算法。在Leukemia数据集上,PTPR最高分类率达到98%左右,并且随着迭代次数s的增加,一直保持较高的分类率;而MC算法的分类率在整体上低于 PTPR算法,且动荡不稳定。在Colon数据集中,对于个别分类器,PTPR和MC得到了同一水平的分类率;但是,从整体来看,PTPR比 MC仍具有一定的提高,PTPR最高达到了 90.0%左右的分类率。对于Glioma数据集,它和Colon数据集类似,所含样本较少,在分类率上和 Colon也具有同样的现象,但PTPR的部分结果仍高于 MC,且 PTPR比 MC更加快速地收敛到较高的分类率并保持稳定,如图10中的NB和SVM所示。在Prostate和Ovarian数据集上,除个别外,PTPR的分类率大多数超过了 MC,尤其是在 Ovarian数据集上,MC只得到65%的分类率,而PTPR却达到了75%。
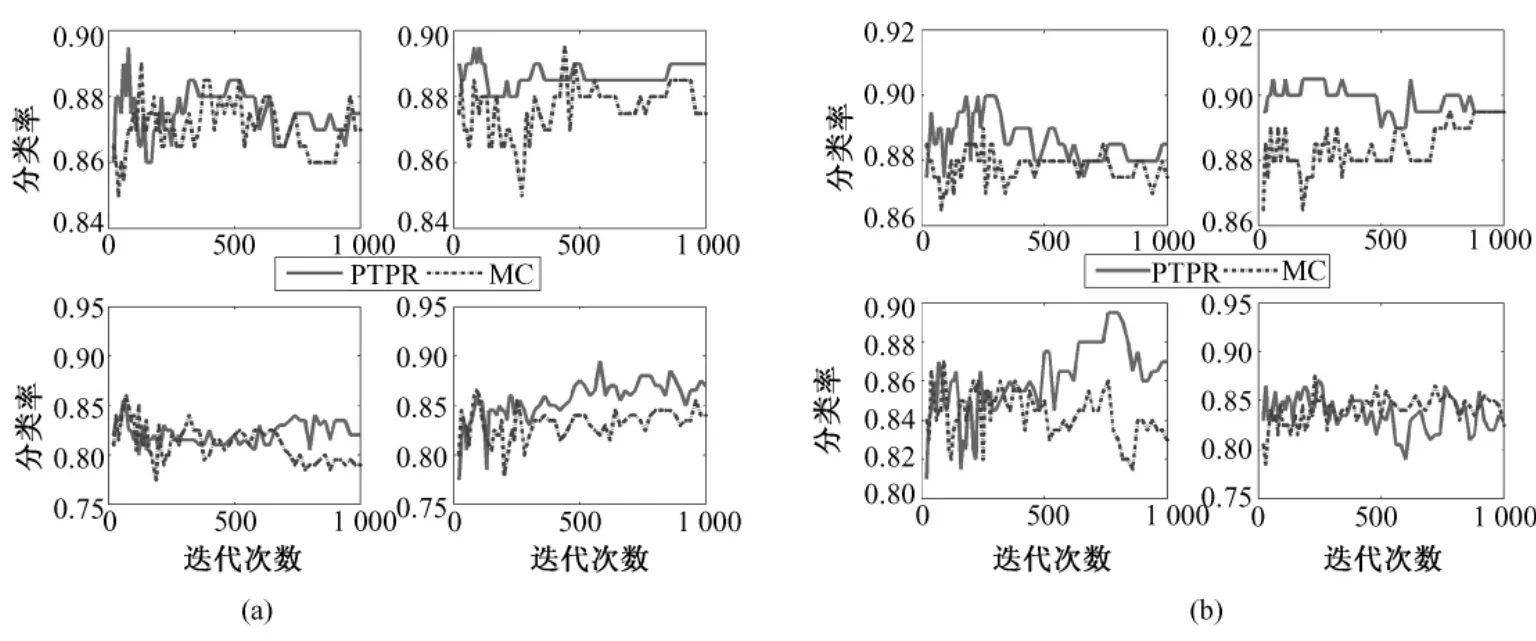
图9 不同基因在NB、SVM、KNN和RF上(从左至右,从上到下)的Colon分类率。(a)10个基因;(b)20个基因;Fig.9 The classification rate of different gene number in NB,SVM,KNN and RF(from left to right,from upper to bottom)for Colon.(a)10 genes,(b)top 20 genes
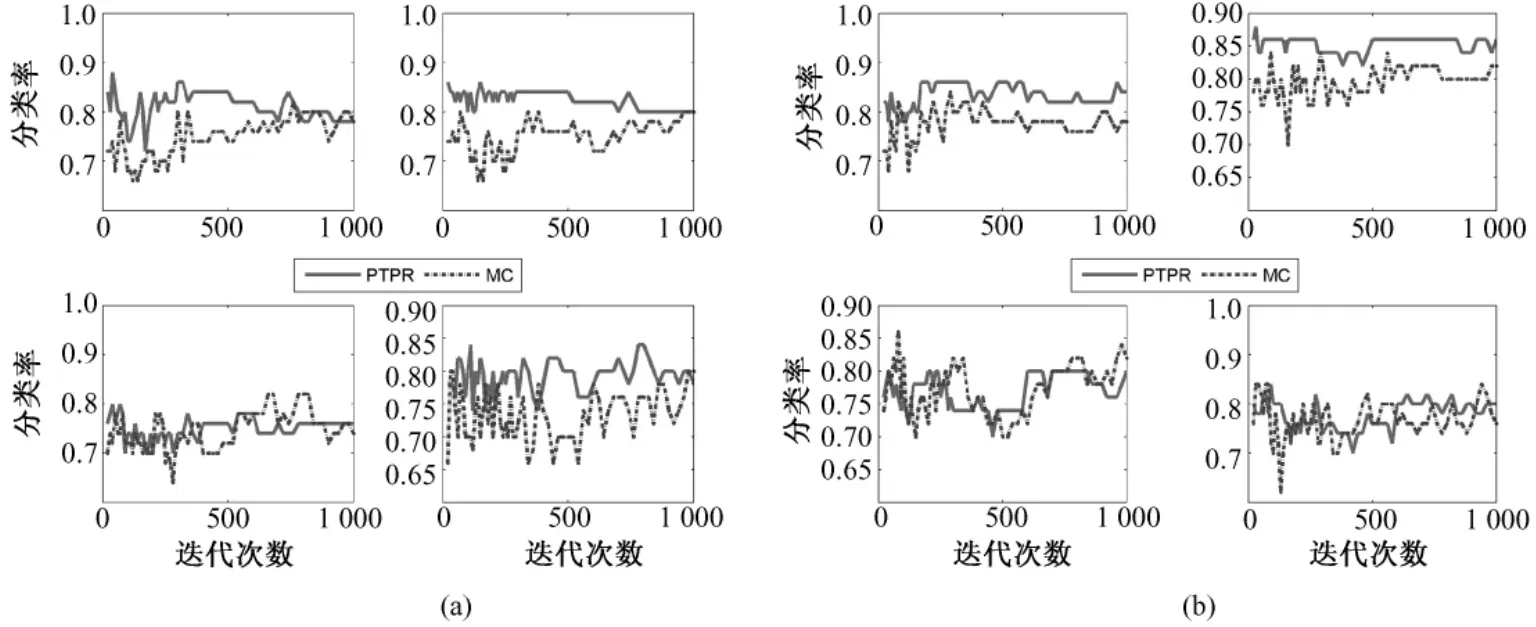
图10 不同基因在NB、SVM、KNN和RF上(从左至右,从上到下)的Glioma分类率。(a)10个基因;(b)20个基因;Fig.10 The classification rate of different gene number in NB,SVM,KNN and RF(from left to right,from upper to bottom)for Glioma.(a)10 genes,(b)top 20 genes
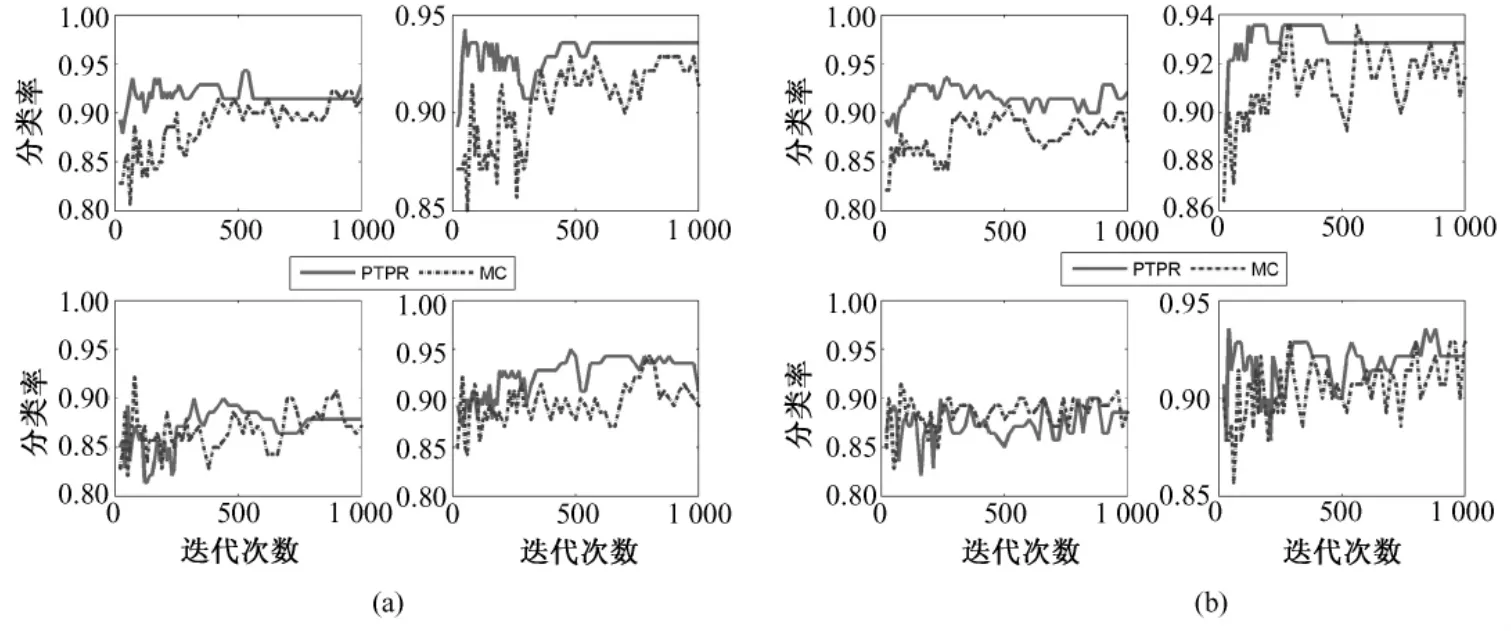
图11 不同基因在NB、SVM、KNN和RF上(从左至右,从上到下)的Prostate分类率。(a)10个基因;(b)20个基因;Fig.11 The classification rate of different gene number in NB,SVM,KNN and RF(from left to right,from upper to bottom)for Prostate.(a)10 genes,(b)top 20 genes
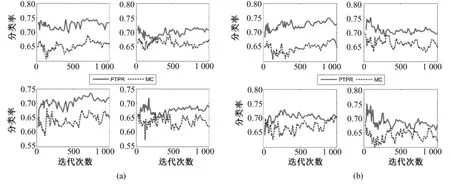
图12 不同基因在NB、SVM、KNN和RF上(从左至右,从上到下)的Ovarian分类率。(a)10个基因;(b)20个基因;Fig.12 The classification rate of different gene number in NB,SVM,KNN and RF(from left to right,from upper to bottom)for Ovarian.(a)10 genes,(b)top 20 genes
因此,从数据集Leukemia、Colon、Glioma、Prostate和Ovarian在不同分类器(NB、SVM、KNN和RF)上的分类率来看,PTPR整体的结果优于MC,不依赖于某一固定的分类器,而且随着迭代次数s的增加,它的分类率保持不变或者增长,动荡幅度小于MC算法。
2.3 其他方法的分类率比较
Leukemia、Colon、Glioma和 Prostate作为公共数据集,已经被广大研究者用来进行研究和分析,并取得了一定的成果。在与其他研究者所用数据和样本比例划分完全一致的条件下,利用PTPR算法提取特征基因,在独立的测试集上进行分类率测试,结果如表2~表5所示。
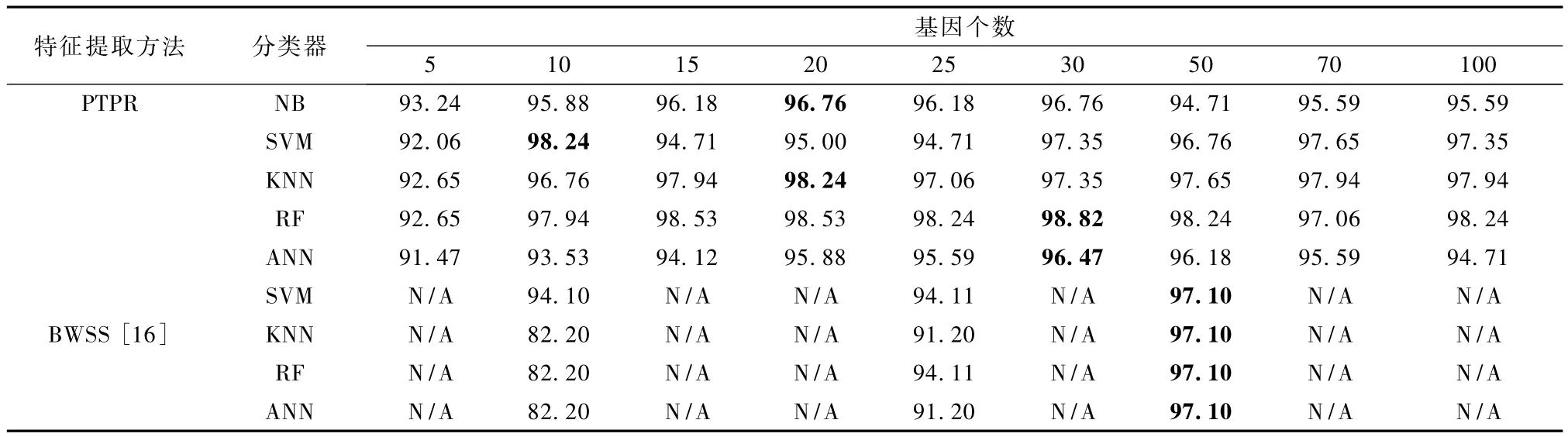
表2 Leukemia-PTPR和其他方法的分类率Tab.2 Classification accuracies for PTPR and other methods on Leukemia %
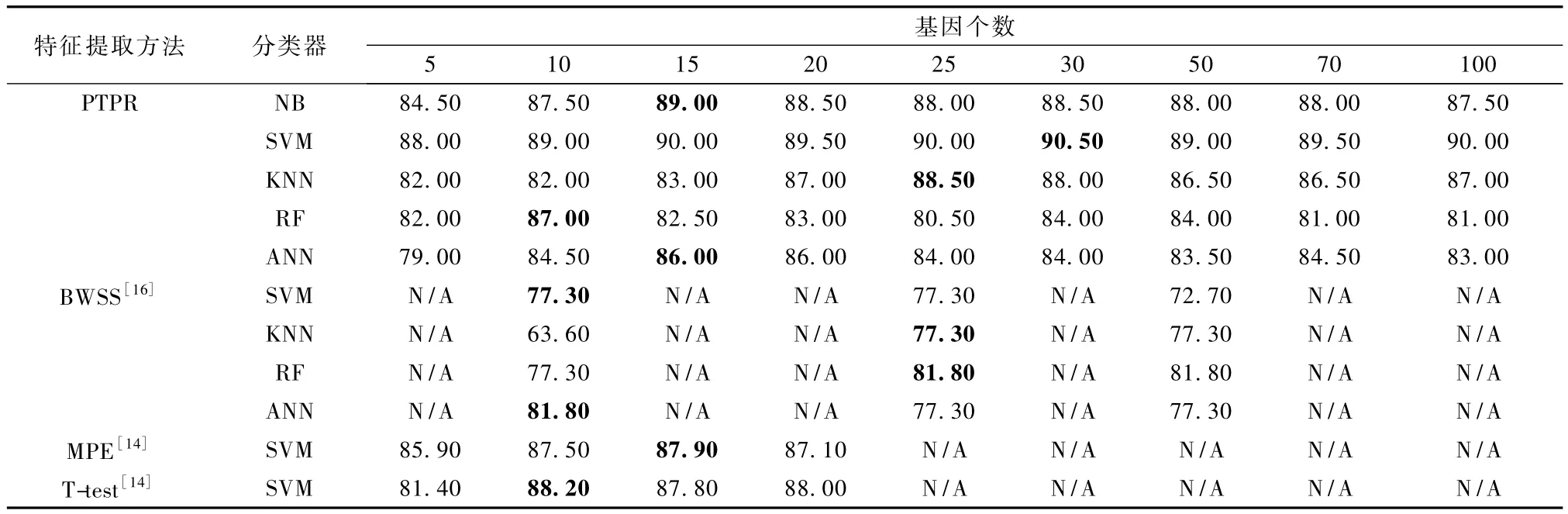
表3 Colon-PTPR和其他方法的分类率Tab.3 Classification accuracies for PTPR and other methods on Colon %
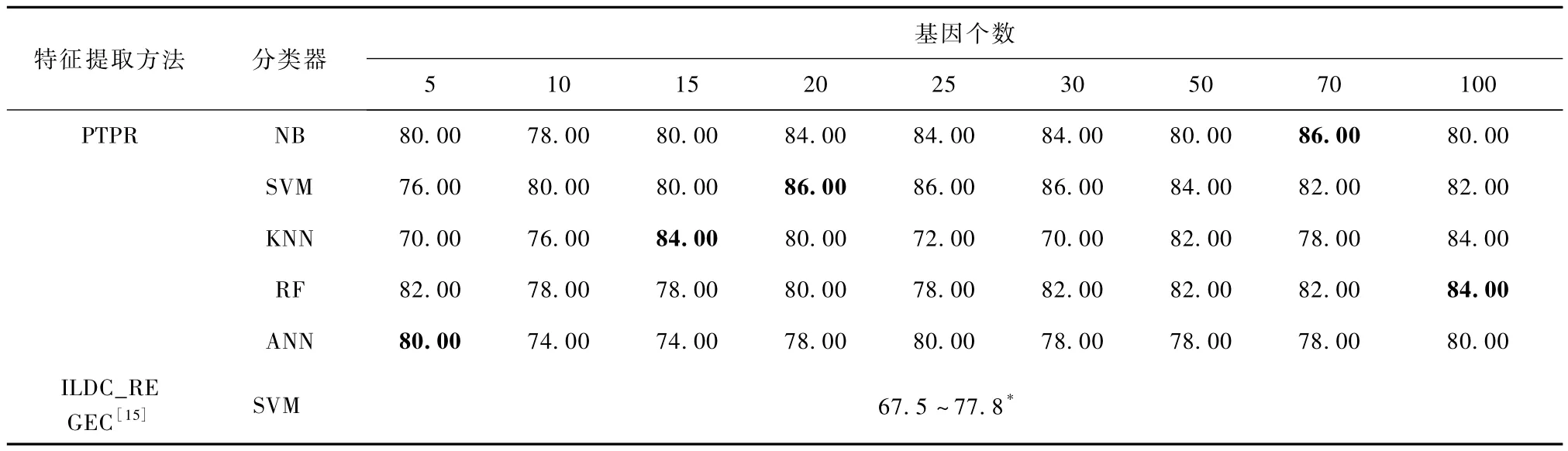
表4 Glioma-PTPR和其他方法的分类率Tab.4 Classification accuracies for PTPR and other methods on Glioma %

表5 Prostate-PTPR和其他方法的分类率Tab.5 Classification accuracies for PTPR and other methods on Prostate %
由表2可以看出,用 BWSS方法提取特征基因[16],在50个基因个数时,4个分类器都取得最高分类率97.10%;而用 PTPR算法所提取的特征基因,在SVM、KNN、RF和 ANN上的分类率最高值分别为在 10、20、30、30个基因处所对应的 98.24%、98.24% 、98.82% 、96.47% 。也就是说,除 ANN 上PTPR所得分类率最高值略低于BWSS方法外,在其他分类器上,PTPR方法在较少基因时得到的分类率都超过 BWSS的最高值97.10%。从整体上来看,PTPR算法在 10个基因时得到 98.24%、97.94%,超过 BWSS方法在 50个基因处的97.10%,而PTPR算法在30个基因上得到了高达98.82%的分类率。因此,从不同基因个数和不同分类器角度来看,所得分类率PTPR算法整体高于BWSS方法,在不同分类器上都保持较高的分类率。
由表 3 可以看出,MPE[14],T-test[14]和 BWSS[16]方法所得到的最高分类率88.20%是在10个基因处SVM分类器上得到,而PTPR算法同样的在10个基因、SVM分类器上得到分类率89.00%,在30个基因上得到最高值90.50%,其他基因个数上的分类率也都在88.00%以上,整体高于88.20%。换句话而言,PTPR算法所得分类率明显高于 T-Test方法。虽然PTPR方法在其他分类器上的结果不如在SVM上高得显著,但是同 BWSS、MPE相比仍处于较优水平。
由表4可以看出,ILDC_REGEC[15]的方法所得到的分类率在不同基因个数上的分类率介于67.5% ~77.8%之间,而 PTPR算法得到的分类率最高达到86.0%,明显高于77.8%。在NB、SVM和KNN上,PTPR所得分类率基本稳定在80.0%以上,明显高于ILDC_REGEC方法,而 ANN上分类率的结果虽然不及其他分类器,但整体仍然较优;在5个分类器上,PTPR方法的分类率最高值全部高于ILDC_REGEC最高值。
在表 5中,ILDC_REGEC[15]方法的分类率位于78.0% ~91.2% 之间,而 PTPR 算法在 NB、SVM、KNN、RF和 ANN上的分类率最高值分别为92.86% 、94.29% 、92.14% 、97.14% 、94.29% ,全部高于ILDC_REGEC方法的91.2%。在5个不同的分类器上,PTPR的分类率整体优于 ILDC_REGEC算法的分类率。
3 结论
PTPR算法在随机搜索算法的基础上,借鉴职业网球选手的排名规则,引入了种子变量、滚动的排名机制,保留了MC算法的优点,即选择基因时,综合利用决策树本身的优点,不是单纯地依靠分类率的高低,而是从基因所含信息量的角度进行选择。除此之外,PTPR算法克服了MC算法搜索效率低、收敛慢的缺点,合理利用了当前最优的变量,提高了筛选效率,使得PTPR算法能够有效地从成千上万个变量中提取出具有显著性差异的基因。通过在不同数据集、不同分类器上的验证,可知 PTPR保持了较强的鲁棒性,所得到的结果不依赖于固定分类器,适用于高维、高噪声、小样本的数据类型特征选择问题,同时能够快速地收敛到稳定的最优解,而且最终得到的分类率明显优于MC以及其他特征提取算法。
附录 Permutation原理及实验设计
为了比较MC和PTPR算法方法所挑选出的基因是否稳定,设计了Permutation实验,计算P-value步骤如下:
· 根据实验目的,得出两组真实数据集如下:
P= [p1,p2,…,pn]和 Q= [q1,q2,…,qn]
·计算真实平均值的差值Δ0=,其中
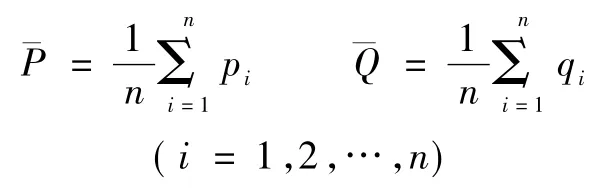
· 混合数据集 P和 Q,随机分成数据集 k次,即
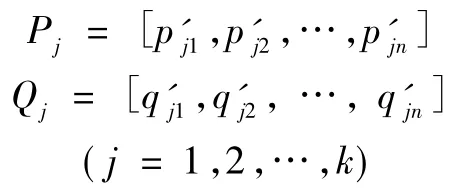
· 计算Permutation数据集平均值的差值,有
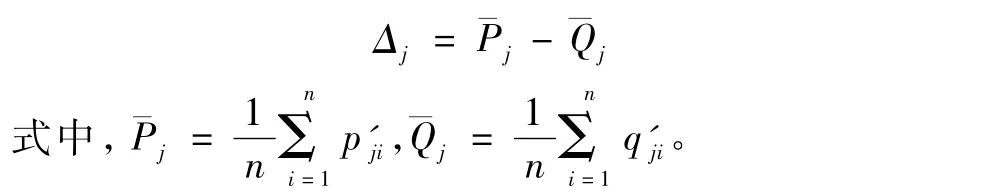
[1]Inza I,Larranaga P,Blanco R,et al.Filter versus wrapper gene selection approaches in DNA microarray domains[J].Artificial Intelligence in Medicine,2004,31:91-103.
[2]Jirapech Umpai T,Aitken S.Feature selection and classification for microarray data analysis:evolutionary methods for identifying predictive genes[J].Bmc Bioinformatics,2005,6:1-11.
[3]Yang Wenzhu,Li Dongling,Zhu Liang.An improved genetic algorithm for optimal feature subset selection from multi-character feature set[J].Expert Systems with Applications,2011,38:2733-2740.
[4]Li Xiongmin,Chan CW.Application of an enhanced decision tree learning approach for prediction of petroleum production[J].Engineering Applications of Artificial Intelligence,2010,23:102-109.
[5]Draminski M,Rada-Iglesias A,Enroth S,et al.Monte Carlo feature selection for supervised classification [J].Bioinformatics,2008,24(1):110-117.
[6]Hamdani TM,Wob JM,Alimi AM,et al.Hierarchical genetic algorithm with new evaluation function and bi-coded representation for the selection of features considering their confidence rate[J].Applied Soft Computing,2011,11:2501-2509.
[7]Mohammadi A,Saraee MH,Salehi M.Identification of diseasecausing genes using microarray data mining and Gene Ontology[J].BMC Medical Genomics,2011,4(12):1-9.
[8]Li Lihua,Chen Li,Goldgof D,et al.Integration of clinical information and gene expression profiles for prediction of chemoresponse for ovarian cancer[C]//Proceedings of Annual International Conference of the IEEE Engineering in Medicine and Biology Society.Shanghai:IEEE,2005:4818-4821.
[9]Guyon I,Weston J,Barnhill S,et al.Gene selection for cancer classification using support vector machines[J].Machine Learning,2002,46:389-422.
[10]Golub TR, Slonim DK, Tamayo P, et al. Molecular classification of cancer:class discovery and class prediction by gene expression monitoring[J].Science,1999,286(5439):531-537.
[11]Alon U,Barkai N,Notterman DA,et al.Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays[J].Proc Natl Acad Sci USA,1999,96(12):6745-6750.
[12]Nutt CL,Mani DR,Betensky RA,et al.Gene expression-based classification of malignant gliomas correlates better with survival than histological classification[J].Cancer Research,2003,63(7):1602-1607.
[13]Singh D,Febbo PG,Ross K,et al.Gene expression correlates of clinical prostate cancer behavior[J].Cancer Cell,2002,1(2):203-209.
[14]Mahata P,Mahata K.Selecting differentially expressed genes using minimum probability of classification error[J].Journal of Biomedical Informatics,2007,40(6):775-786.
[15]Guarracino MR,Cuciniello S,Pardalos PM.Classification and Characterization of Gene Expression Data with Generalized Eigenvalues[J]. Journal of Optimization Theory and Applications,2009,141(3):533-545.
[16]Chakraborty S. Simultaneous cancer classification and gene selection with Bayesian nearest neighbor method:An integrated approach[J].Computational Statistics& Data Analysis,2009,53(4):1462-1474.
