基于Shapley-Value的梯级水库联合调度效益分配方法探讨

杨春花，杜康华

（1.长江科学院水资源综合利用研究所，武汉 430010；2.三峡水力发电厂，湖北宜昌 443009）

基于Shapley-Value的梯级水库联合调度效益分配方法探讨

杨春花1，杜康华2

（1.长江科学院水资源综合利用研究所，武汉 430010；2.三峡水力发电厂，湖北宜昌 443009）

目前梯级水库在联合调度时由于补偿效益分配制度上的不合理，致使一些调节性能较好的电站在联合调度过程中得不到公正的对待，从而影响了这些电站对联合调度的积极性。针对上述问题，以三峡梯级和清江梯级五库联合调度为例，引入博弈论中的Shapley-Value法对联合调度所产生效益分配方法问题进行了探讨。结果表明：该方法不仅具有很强的操作性，并且在分配过程中充分考虑了调节性能好的清江梯级在系统参与调峰过程中的效益补偿，其分配结果对各参与方都是公平合理的，从而使各梯级都有参与合作的积极性，有利于实现梯级水库群总效益最优的目标。

梯级水库；联合调度；Shapley-Value；效益分配

1 概 述

水电是清洁能源的、可再生的能源，具有巨大的市场前景。国家电力十二五规划中强调，要优先开发水电，将其放在第一位。单一水电站参与电网供电，则缺乏竞争力，特别是调节性能弱的水电站，只有将流域的水电站群以整体的形式统筹调度才能体现水电的优势［1］。目前我国诸多河流都进行了梯级水能开发，但是由于还没有形成一套完全合理适用的梯级电站联合调度补偿效益分配办法，致使一些坝高、库大及调节性能较好的电站效益得不到公正的评价和肯定，从而制约了调节性能好的电站对梯级水库联合调度的积极性，在一定程度上也影响了我国水电事业的发展。因此，科学合理的效益分配方法是我国梯级水电开发急需考虑的问题。

本文采用博弈论中的Shapley-Value来解决梯级水库联合调度后效益分配问题，此方法可实现公平和有效的分配共同效益，从而促进梯级水库联合调度的顺利开展。

2 博弈模型的均衡启示

2.1 博弈模型

假设有2家厂商生产有差异的同类产品供应同一市场，现在它们正面临是否合作的问题。为了模型建立的方便，假设a，b分别为各自单干的利益，并假设只要厂商选择单干，他的利益就保持不变；Δ为参加联盟所增加的利益，Δ＞0且不一定相等，这些假设并不影响博弈的结果。根据Nash均衡定义，该博弈过程存在2个结果：（合作，合作）和（不合作，不合作），对应的盈利分别为（a＋Δ，b＋Δ）和（a，b）。

2.2 分析及启示

由博弈的定义可知，一个博弈需要设定4个方面，其中之一就是博弈方的得益。博弈中每个局中人作出的理性决策的重要依据之一就是他可能的收益有多少，盈利函数的结构与取值无疑将会影响到局中人的行为，因而影响到博弈的最终结局。从Nash均衡结果知道，当局中人在“集体理性”的假设前提下，必然会选择第一种均衡：（合作，合作），因为合作带来的收益大于单干所获得的收益。但是，在“个体理性”的假设前提下，并不排除第二种情况的可能。如何消除“个体理性”，关键之一就是在联盟博弈利益分配中，使局中人感觉到利益分配的公正性。只有当各局中人将自己的收入-付出与其他人的收入-付出比率相比较后，得出的比率值相同时，各局中人才会感到公平，才会加入联盟，并促使联盟的稳定，否则他们将会离开联盟。

3 Shapley-Value法

Shapley-Value是N人联盟博弈理论中一种解的概念，它实现了联盟总体利益在各成员之间的公平和有效的分配。在2个或2个以上的决策者参与合作时的合作收益大于其各自独立行动所得的收益总和时，每个参与者都希望从合作收益中获得自己满意的比例。假设有N个参与人（水库）参与合作，S是N的子集，v（S）是｛S｝联合体（联盟）的特征函数，表示联合体S通过协调其成员的策略所能获得的最大利益；可以把总收益v（N）按这样一种方式分配给各参与人，使之不仅满足个体合理性和群体合理性，而且还满足联盟合理性，即任何联合体中的成员在这种分配方式下的所得都不小于他独立出来时的所得，因此也就没有意愿拒绝这样的分配，这样的分配方式是公平合理的，该分配方式即Shapley-Value方法［2－4］。

Shapley-Value方法是一种公理化方法，它可以得到合作对策唯一解。假设Φi（v）为局中人i在对策（N，v）中应该得到的期望收益，若T是（N，v）的一个联盟，如果对于任意的联盟S，均有v（S∩T）＝v（S），则称T为这个对策的一个载体。假设π是N的一个排列，定义对策（N，πv）为这样一个新对策（N，u），对于任意联盟S＝｛i1，i2，…，is｝，有u（π（i1），…，π（is））＝v（S）。

1953年，Shapley提出合作博弈中合理分配的Shapley-Value 3个公理，其基本思想如下：

公理1（有效性）：如果成员i对他所参加的任一合作都无贡献则给他的分配应为0，如果T是对策v的一个载体，则

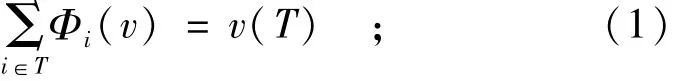
公理2（对称性）：参与人因合作而分配到的利益与他被赋予的记号i无关，各参与人的收益之和等于全体的合作获利。对于N的任一排列π，有

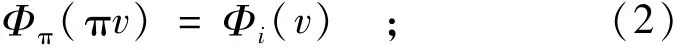
公理3（线性性）：即如果N人同时进行2项合作时，每人的总分配分别是2项合作的分配之和。如果u，v∈G，0≤p≤1，则

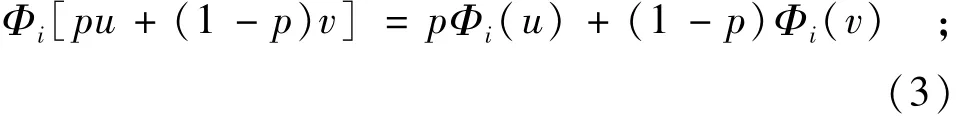
若满足以上3个公理，则Shapley-Value存在唯一解为

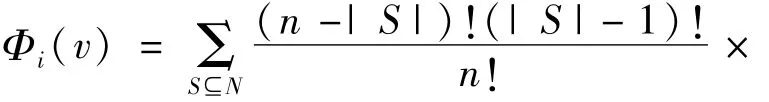
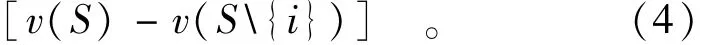
其中｜S｜表示联盟中所含局中人个数，（S＼｛i｝）集合表示S中除了i之外其他成员组成的联盟。

Shapley-Value是根据局中人对联盟｛S｝所做的边际贡献的大小来分配支付的，体现了某种程度上的公平性和合理性。对于2个参与人时的Shapley-Value效益分配按下式计算：

式中，Φ1（v），Φ2（v）分别表示第1个和第2个参与人按照Shapley-Value法从最大的合作效益中分得的份额。v（a），v（b）分别表示第1个和第2个参与人单独运行时获得的效益，v（ab）表示2个参与人合作时获得的总效益。

在参与联合调度双方获得大于其单独调度的效益，并且在分配机制公平合理的情况下，各梯级才有积极性参与合作。Shapley-Value分配方法不仅衡量了各局中人的平均贡献，而且提供的分配具有联盟稳定性，或者说任何一个局中人都不愿意单方面离开该联盟体。该方法可使各参与者都能够从合作中得到与自身贡献相应效益，从而使合作各方均乐于参与。

4 实例研究

本文以清江-三峡梯级联合调度为例，针对分属2个不同发电集团的梯级水电站联合调度效益分配问题，应用Shapley-Value法进行探讨，试图寻求一种相对公平、合理的分配方式，以实现联盟的稳定及整个梯级水库群系统总效益最优的目标。

4.1 系统概况

本系统包括三峡梯级和清江梯级共5座水电站，其中三峡梯级包括三峡和葛洲坝2座水电站；清江梯级有水布垭、隔河岩和高坝洲3座水电站。三峡梯级紧邻清江梯级，清江梯级河口在三峡梯级中葛洲坝电站下游约40 km处，2梯级水库位置概化图如图1所示。

三峡梯级是我国目前最大的梯级水电站群，三峡水库只具有不完全年调节能力，葛洲坝是三峡水库的反调节水库，具有日调节能力，两者总装机容量为2 091.5万kW，梯级保证出力为499万kW，多年平均发电量为986亿kW·h（设计值）。清江梯级总装机330.4万kW·h，梯级保证出力61.8万kW，多年平均发电量75.88亿kW·h（设计值），其中水布垭为多年调节，隔河岩为年调节，高坝洲水库为日调节。清江梯级电站调节性能好，特别是龙头电站水布垭，是华中电网中不可多得的具有多年调节性能的水库，同时也是距三峡梯级最近的调峰、调频和保证安全的大型水电站。目前三峡梯级和清江梯级分属于2个电力公司。三峡梯级的管理单位是中国长江三峡工程开发总公司，清江梯级的管理单位为湖北清江水电开发有限责任公司，2公司单独进行运行管理。

一些专家学者曾对三峡-清江梯级联合调度进行了研究。陈洋波等对隔河岩和高坝洲梯级水电站水库联合调度方案进行了研究［5］；高仕春等以发电量最大和保证出力最大为目标，建立了梯级单独调度和系统联合调度数学模型，计算了系统联合调度后的补偿效益［6］；张文选等采用常规调度方法初步分析了三峡梯级与清江梯级水库联合调度补偿效益［7］；刘宁以三峡梯级与清江梯级所组成的混联式水电站群进行联合调度研究，寻求出了梯级水库群最佳组合调度方式［8］。

4.2 清江-三峡梯级模式

由于清江-梯级3个电站由清江公司统一管理，三峡电站、葛洲坝电站由三峡公司统一调度。因此本文不对5座电站的单独调度情况进行分析，仅对清江梯级和三峡梯级2个子系统的单独调度和联合调度2种模式进行探讨。在清江-三峡梯级大系统中，由于清江上游水布垭电站具有多年调节能力，可根据预报的来水情况优化自身的放水策略，中游隔河岩电站有年调节能力，按照水布垭出库和区间来流情况进行优化，下游高坝洲为径流式电站，在中长期优化调度模型中只考虑利用其水头发电；三峡电站按上游预报来水情况调度，葛洲坝为三峡的反调节电站，无调节能力，按水头发电。

（1）模式一为清江-三峡2个子系统单独优化。水布垭电站根据预报的来水情况，与隔河岩、高坝洲作为一个统一的利益集团，各水库在满足综合利用要求的前提下，使清江集团效益最大；三峡电站也根据上游来水与葛洲坝电站一起归属三峡集团统一优化调度，使三峡集团的效益最大。

（2）模式二为清江-三峡2个子系统联合调度。由于2个子系统为并联系统，所以在满足2个子系统优化模型的约束条件的前提下，下游综合利用用水约束中要求下游宜都流量为2个梯级系统时段平均出力对应流量之和，使三峡-清江这个统一的大系统效益最大。

具有独立决策的水库，其采用何种模式进行调度主要取决于在该模式中能够获得更大的实际收益，且各合作方都认为收益分配是公平、合理的，否则有些参与人宁愿不合作。在梯级调度模式的选择上，最上游水库和具有较大调节能力的水库有更大的主动权，日调节或无调节水库处于从属地位。

4.3 各模式效益及结果分析

本文提出的2种调度模式的计算效益采用刘宁在《三峡-清江梯级电站联合优化调度研究》一文中的研究成果，如表1所示。

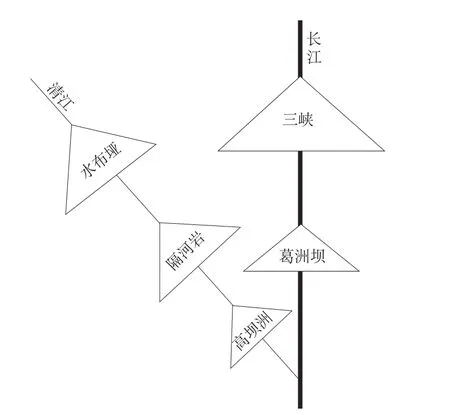
图1 三峡梯级与清江梯级概化图Fig.1 Generalized diagram of Three Gorges cascade and Qingjiang cascade reservoirs

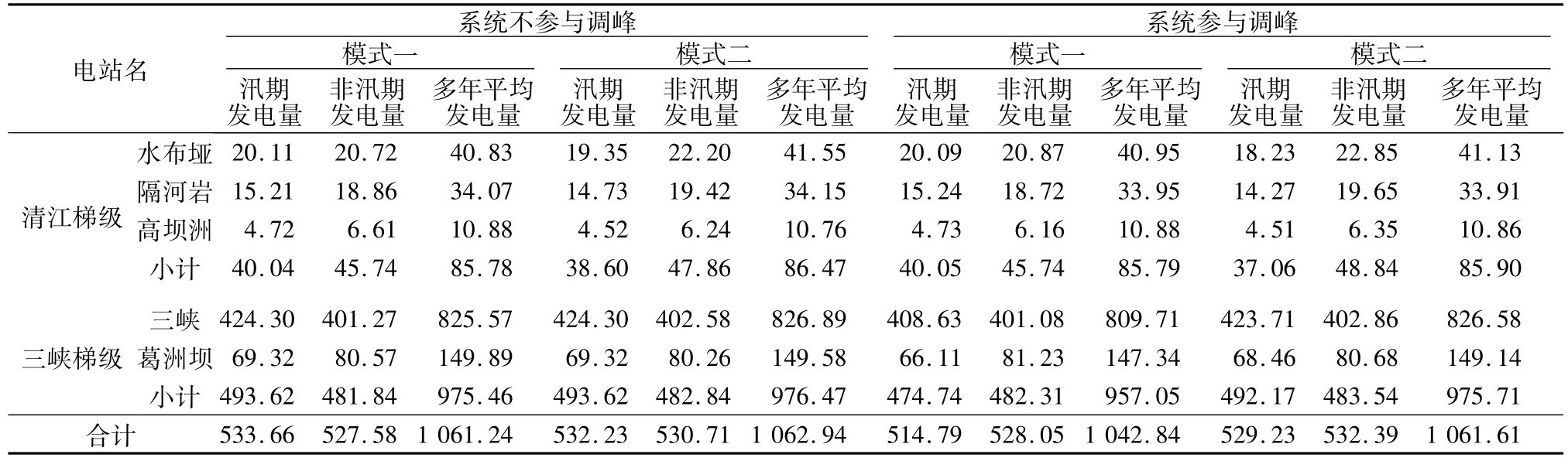
表1 三峡梯级、清江梯级各模式下发电量计算结果Table 1 Calculated results of electricity generation by Three Gorges and Qingjiang cascade reservoirs in each mode 108kW·h

从清江梯级和三峡梯级在2种调度模式下的发电效益来看，模式二较模式一的效益更好。但仅仅是系统联合运行下的效益大于单独运行，并不足以作为双方进行联盟的理由。联合调度产生的收入如何在各水库间进行公平、合理的分配，才是各参与双方是否愿意合作的核心问题，如果某个参与者认为其获得的实际收益与它所创造的价值不匹配，所得的份额过小时，它将对合作也会产生抵触情绪，甚至退出合作，因此，选择合理的分配方式使联盟得以持续进行至关重要。

4.4 清江-三峡梯级联合调度利益分配

4.4.1 利益分配

水库群联合优化调度可以得到比他们单独调度更好的经济效益，因此联合优化调度的分配问题可以用合作博弈进行分析和求解。根据清江梯级和三峡梯级在2种模式下的效益情况，应用Shapley-Value法，计算出2梯级在合作运行时的利益分配方案，计算结果如表2。

表2 三峡梯级、清江梯级各模式下所得效益及Shapley值分配Table 2 Electricity distribution for Three Gorges and Qingjiang cascade reservoirs in each mode calculated by Shap ley valuemethod 108kW·h

4.4.2 结果分析

由表2中三峡梯级、清江梯级在各模式下的效益及Shapley值分配结果，可以得出如下结论：

（1）在系统不参与调峰时，清江梯级在单独调度时所得到的效益是85.78亿kW·h，在联合调度并按Shapley-Value分配得的效益是86.63亿kW·h；三峡梯级在单独运行时的效益为975.46亿kW·h，在联合调度按Shapley-Value分配的效益为976.31亿kW·h；在系统参与调峰时，清江梯级在单独调度时所得到的利益是85.79亿kW·h，在联合调度并按Shapley-Value分配得的效益是97.175亿kW·h；三峡梯级在单独运行时的效益为957.05亿kW·h，联合调度按Shapley-Value分配的效益为966.435亿kW·h。由此可以看出，无论系统是否参与调峰，清江梯级和三峡梯级在联合调度中的发电效益均比单独调度效益大。

（2）清江梯级在系统不参与调峰时按Shapley-Value的分配比为8.15%，在参与调峰后其分配比增加到8.97%；三峡梯级在系统不参与调峰时的分配比为91.85%，而其在调峰后的分配比减少为91.03%。其主要原因是按Shapley-Value分配方法考虑到系统在汛期调峰时，三峡梯级主要承担电网中的基荷部分，调频、调峰任务由清江梯级完成，而清江梯级由于在汛期调峰，产生大量弃水，所以其发电效益要小于不调峰时产生的效益，所以按Shapley-Value分配结果可看作为是对清江调峰效益损失的一种补偿。因此Shapley-Value分配方式无论对清江梯级还是三峡梯级都是可以接受的，该分配方式能充分考虑了清江系统中水布垭和隔河岩这2个电站在电网中的调峰贡献，较之与其他的补偿分配方式［9］要合理得多。

（3）Shapley-Value法为合作所带来的效益提供了较为公平、合理、可操作的分配方法，使合作者都能够从合作中得到与自身贡献相应的效益，而且该方法无论哪一参与人制定都得到相同的结果，使合作者之间不会出现由于算法原因出现合作不愉快的现象，合作的各方均有合作的积极性，使合作能够形成并可以持续进行。

5 小 结

由于电网系统的复杂性，分期电价的差异性及水文现象的变异性，使得不同发电集团的梯级电站联盟效益分配问题也比较复杂。本文没有考虑电价等诸多因素影响，只是从多年平均发电量这个角度，以清江-三峡梯级水库群为例，应用Shapley-Value法对2种模式下清江三峡梯级的联合调度效益分配问题进行了探讨。

在该分配策略下，既能使联合梯级的总效益增加，特别是参与系统调峰时总效益增加1.8%，又能兼顾公平合理的原则，调动各方参与的积极性，促进梯级水库群集中联合调度，进一步增强了流域中各水库的水能补偿作用，提高梯级水电群的整体经济效益、优化人力资源管理，使我国的水利事业得到可持续发展。

［1］ 《湖北水力发电》编辑部.湖北省院士、专家建言献策——倡议进行三峡梯级和清江梯级五库联合调度研究［J］湖北水力发电，2007，（5）：1－2.（Editorial Office of Hubei Water Power.Suggestions of Academicians in Hubei Province——Suggest on the Integrated Operation of Hydropower Station Groups of Three Gorges Cascade and Qingjiang Cascade［J］.HubeiWater Power，2007，（5）：1－2.（in Chinese））

［2］ 占辉斌，郭锦墉，詹海斌，等.Shapley-value法在战略联盟利益分配中的应用［J］.商业研究，2005，（19）：35－37.（ZHAN Hui-bin，GUO Jin-yong，ZHAN Haibin，et al.The Application of Shapley-value in Gains Distribution of Strategic Alliance［J］.Commercial Research，2005，（19）：35－37.（in Chinese））

［3］ YOUNGSUB CHUN.A New Axiomatization of the Shapley Value［J］.Games and Economic Behavior，1989，1（2）：119－130.

［4］ GENJIU XU，DRIESSEN THEO SH，MATRIX H S.A-nalysis for Associated Consistency in Cooperative Game Theory［J］.Linear Algebra and Its Applications，2008，428（7）：1571－1586.

［5］ 陈洋波，胡嘉琪.隔河岩和高坝洲梯级水电站水库联合调度方案研究［J］.水利学报，2004，35（3）：47－52.（CHEN Yang-bo，HU Jia-qi.Study on Integrated Operation of Cascade Hydropower Stations［J］.Journal of Hydraulic Engineering，2004，35（3）：47－52.（in Chinese））

［6］ 高仕春，万 飚，梅亚东，等.三峡梯级和清江梯级水电站群联合调度研究［J］.水利学报，2006，37（4）：504－507.（GAO Shi-chun，WAN Biao，MEI Ya-dong，et al.Cooperating Dispatch of Hydropower Station Groups of Three Gorges Cascade and Qingjiang Cascade［J］.Journal of Hydraulic Engineering，2006，37（4）：504－507.（in Chinese））

［7］ 张文选，张雪桂.三峡梯级与清江梯级联合调度补偿效益初探［J］.湖北水力发电，2007，（2）：31－34.（ZHANG Wen-xuan，ZHANG Xue-gui.Complementary Benefit Study of United Operation in Three-Gorges and Qingjiang Cascade Hydropower Stations［J］.Hubei Hydropower，2007，（2）：31－34.（in Chinese））

［8］ 刘 宁.三峡－清江梯级电站联合优化调度研究［J］.水利学报，2008，38（3）：264－271.（LIU Ning.Unified Optimal Operation of Three Gorges and Qingjiang Cascade Hydropower System［J］.Journal of Hydraulic Engineering，2008，38（3）：264－271.（in Chinese））

［9］ 傅 春，胡振鹏.一种综合利用水利工程费用分摊的对策方法［J］.水利学报.2000，（4）：57－63.（FU Chun，HU Zhen-peng.A Game Analysis Approach of Cost Allocation for Multipurpose Water Projects［J］.Journal of Hydraulic Engineering，2000，（4）：57－63.（in Chinese） ）

（编辑：王 慰）

An Approach of Benefit Distribution for Joint Operation of Cascade Reservoirs Based on Shap ley-Value M ethod

YANG Chun-hua1，DU Kang-hua2
（1.Yangtze River Scientific Research Institute，Wuhan 430010，China 2.Three Gorges Hydropower Plant，Yichang 443009，China）

Hydropower plantswith good regulating performanceweremade reluctant to be engaged in the jointoperation of cascade reservoirs because of institutional irrationality in the distribution of compensation benefits for the reservoirs.Shapley-Value method of game theory was used to explore the approach of benefit distribution.The Three Gorges and Qingjiang cascade reservoirswere selected as case study.The resultmanifested that thismethod was practicable.The compensation for Qingjiang cascade reservoir which has good regulating performance was fully considered in the system of compensation.Fair and reasonable distribution could be achieved so that the reservoirs could take active cooperation to boost an optimal benefit for all the reservoirs.

cascade reservoir；joint operation；Shapley-Value；benefit distribution

TV697

A

1001－5485（2011）12－0053－05

2011-10-20

中央级公益性科研基金资助项目（CKSF2010004，CKSF2011001）

杨春花（1985-），女，江西九江人，助理工程师，主要从事水文学及水资源开发利用研究，（电话）027-82828051（电子信箱）ychh1985＠126.com。