基于穷尽熵优化的混沌图像加密

宁 磊， 王振永， 杨明川

(哈尔滨工业大学 通信技术研究所，哈尔滨 黑龙江 150001)

0 引言

随着世界范围的数字图像传输的迅速发展，安全问题成为了人们关注的重要问题。许多诸如电缆电视，军用图像数据库，生物测量鉴定系统以及在线个人照片相册要求具有鲁棒安全性的系统来存储和传输数字图像。

传统的密码学算法诸如DES、IDEA和RSA算法不能很好的适用于快速通信应用。而混沌的显著特点是对初始值的敏感依赖性，这使得混沌系统成为密码学方案的一个有前景的另一种选择。基于混沌的加密处理在 1989年[1]被首次提出，从那时开始，许多基于混沌系统的其他方案相继被提出。

许多密码学系统的安全性都是基于随机数发生器。产生随机序列的发生器能够归纳为2大类：真实随机数发生器和伪随机数发生器。真实随机数发生器具有非确定信源的优势，比如随着放射性延迟时间殆尽的热射噪声源，混沌电路以及半导体容量管理数量等。伪随机数发生器通过系统模型产生随机数，产生的随机数随机性较弱，容易攻克。近年来，数字电路的广泛发展使得后者实现的成本变得低廉。这就需要找到一种增强伪随机数发生器伪随机性能的方法。

图像加密的思想可归结为3大类：象素置乱法[2]、位置置乱法[3]和前2类方法的结合[4]。其中象素置乱就是将某个序列与象素值进行某种相关运算，如异或运算。解密过程也很简单，只要用原始序列与加密图像的象素值进行相关逆运算即可。

我们知道作为加密序列，不仅穷尽步长要大，而且穷尽过程的每个组成部分中的序列长度要尽量相等。为此，提出用穷尽熵来衡量序列的类随机性强弱，选择经过熵选择即优化后的混沌序列采用象素置乱法对图像进行加密。最后，安全分析表明此加密方案具有对抗已知统计性攻击的鲁棒性。

1 序列的穷尽熵

序列穷尽熵的概念是建立在序列的生成和再生的基础上提出的。序列的生成和再生是不同的。再生是序列自我的简单复制过程，而序列的生成中复制序列的最后一个序列值是可以变化的。具有强伪随机性的序列，不仅穷尽步长要大，而且穷尽过程的每个组成部分中的序列长度要尽量相等。文献[5]提出了一种利用穷尽熵衡量序列随机性强弱的方法。将序列的各个穷尽部分(包括最后一个不是穷尽的组成部分)在整个序列中占的比率近似地看作其出现的概率 ，然后用式(1)：

来计算整个序列的类随机性强弱。由序列穷尽的概念和最大熵定理可知，序列穷尽步长越长，各穷尽组成部分的概率越是近似相等，则整个序列的穷尽熵越大，序列的类随机性也就越强。

例如：

根据表达式（1），序列S1,S2,S3的穷尽熵分别为 0.0243哈特、0.0486哈特和0.1826哈特。穷尽熵越大，序列携带的信息越多，进而序列的随机性就越强。

2 混沌序列的产生

混沌系统模型有很多种，我们选择比较典型的 Lorenz混沌系统作为混沌序列发生器，它的数学表达式如下：

在表达式（2）中，a、b和c是系统参数，当a=10、b=8 3和c=28时, 保证 Lyapunov 指数λn＞0。系统处于混沌状态。

Lorenz系统可以产生三维混沌实序列，我们只取其中一维。由于其产生的是随机实数，作为加密序列，还需要对混沌序列进行二值量化。文献[6]提出了很多种量化方法，为了方便，将利用表达式（3）将实数序列映射到[- 0.5,0.5]之间，然后通过表达式（4）获取二值序列。

在上述表达式中，bn是由Lorenz系统产生的混沌序列，int(bn)是对序列bn取整运算，Bn是量化后的二值序列。

3 熵优化的混沌序列及图像加密

3.1 序列性能测试

候选的加密序列必须具有较强的伪随机性。首先通过Lorenz系统产生原始的混沌序列，二值量化后，分成N组，通过计算穷尽熵，选择熵最大的一组作为测试序列。该序列的自相关和互相关特性如图1所示。

我们可以看出，其自相关函数接近δ函数，互相关函数接近零函数，这种良好的相关性，是对图像进行加密的前提。

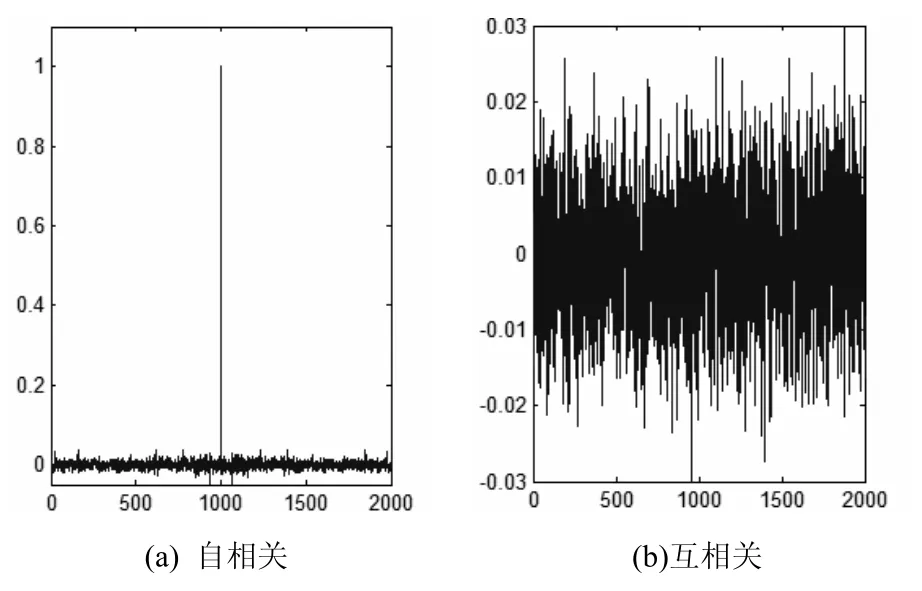
图1 混沌序列的相关性分析

3.2 加密和解密方案

所提出的基于异或函数的图像加密和解密方案在MATLAB中予以实现。该方案包括以下步骤：

①该方案首先找到明文图像的大小为M×N，此处M表示图像的行数，N表示图像的列数，这些像素点被按照从左到右从上到下的顺序排列，由此得到一个该图像的数据集，其中的每项都是像素点的一个十进制灰度值（从0到255），然后将每个十进制数值转换成等价的二进制数，最终得到一个一维矩阵B。

②矩阵A_candidate(n)是基于Lorenz混沌系统产生的二值序列，n代表候选序列的组数，利用穷尽熵的定义选择熵最大的一组作为优选混沌序列A。

③将A和图像矩阵B经过异或运算得到了第三个矩阵C，即C=A⊕B。

④这样得到的矩阵 C通过第一步的相反过程转换为一个加密编码后的图像，作为密文进行传输；

对于图像的解密我们再次采用异或函数进行运算，即C⊕B=A。在图2中我们可以看到大小为131× 131的Lena明文图像，以及采用以上方案得到的加密后的密文图像和解密后的明文图像。

图2 图像加密恢复过程

4 安全性分析

一个好的加密方案应该具有鲁棒性抵抗所有的密码分析，统计性和穷举攻击。文章完成了所提出的图像加密方案的一些安全性分析—柱形统计图分析和2个相邻像素的相关分析。

4.1 柱形统计图分析

香农提出扩散和混淆的两种方法用来防止统计性攻击[7]。明文Lena图像和所提出方案获得的加密图像的柱形统计图如图 3所示。比较柱形统计图我们可以看出加密图像的灰度值呈现均匀分布，其和明文图像的柱形统计图具有明显不同。所以，加密后的图像对于任何的统计性攻击都具有安全性。

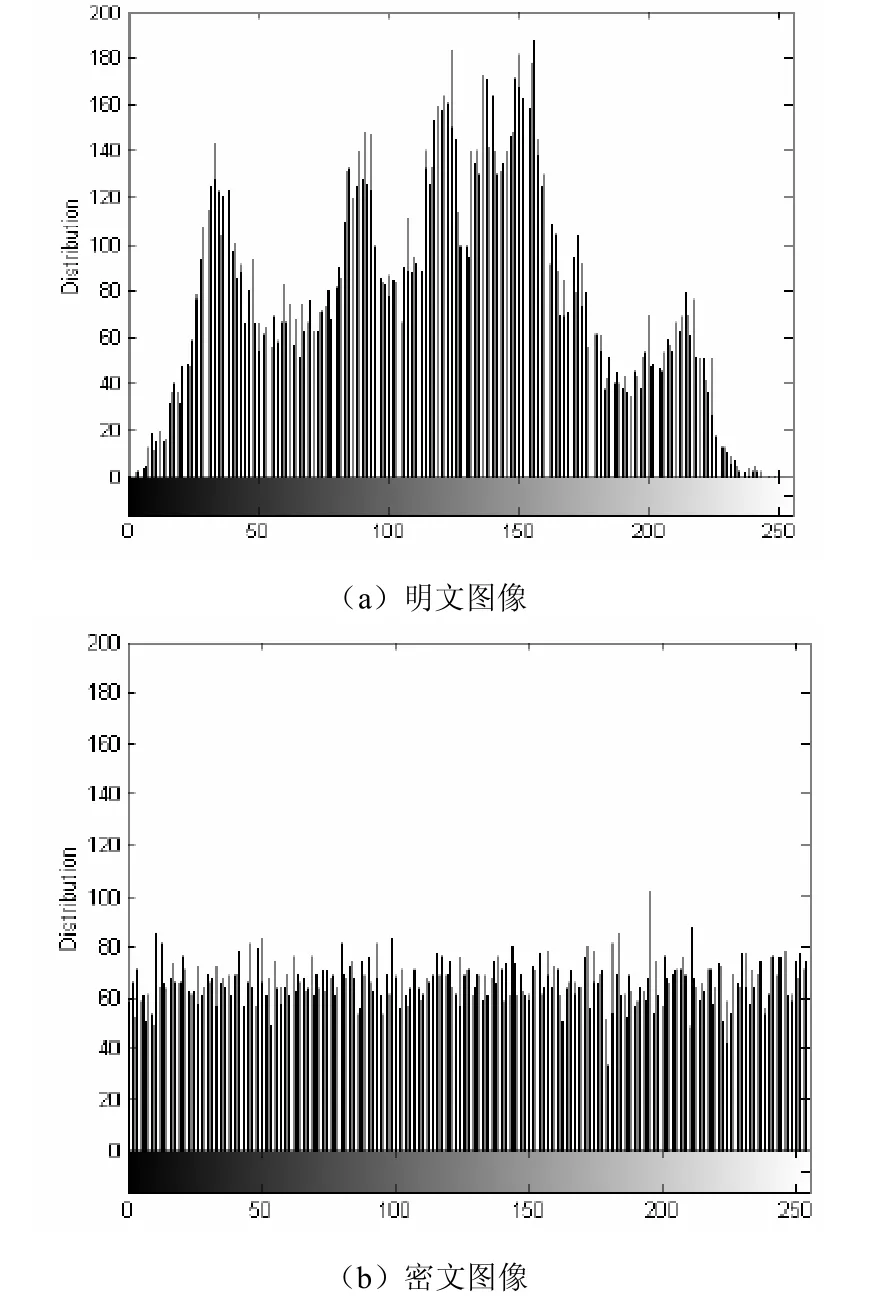
图3 图像柱状统计

4.2 2个相邻像素的相关分析

对于任意一个图像，每个像素点无论在水平方向，垂直方向或者对角方向都与其相邻的像素点高度相关。为了测试在明文图像中像素点的相关性，以及在加密图像中像素点的相关性，我们利用以下公式计算了每个像素对的相关系数γ[8]。

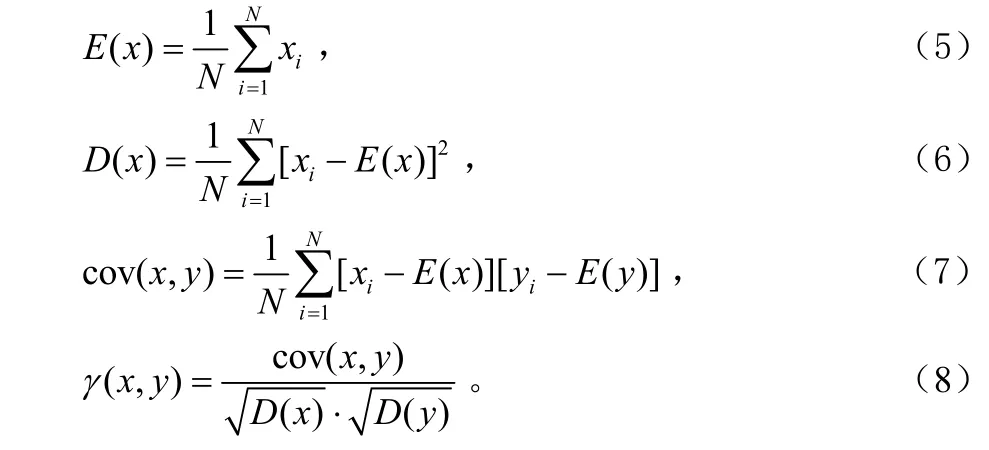
这里x和y是图像中2个相邻像素点的灰度值，N是像素点相邻像素对的总个数。在明文图像和密文图像中的2个水平相邻像素点的相关性如图4所示。

在表1中我们发现密文图像的在任意方向的相关系数都近似等于零，所以密文图像具有很小的关联性。

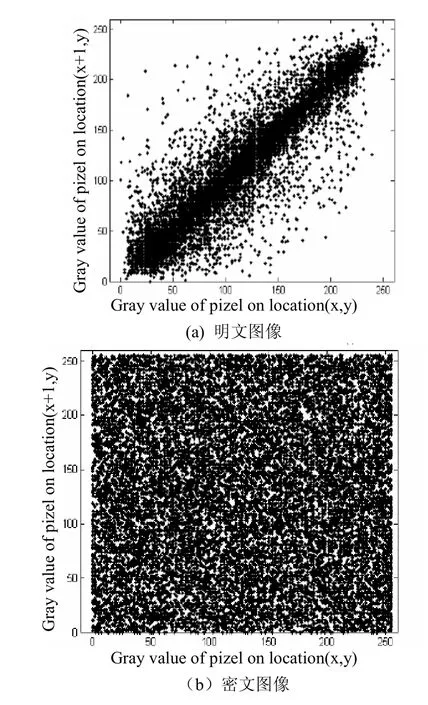
图4 图像中相邻两像素的相关

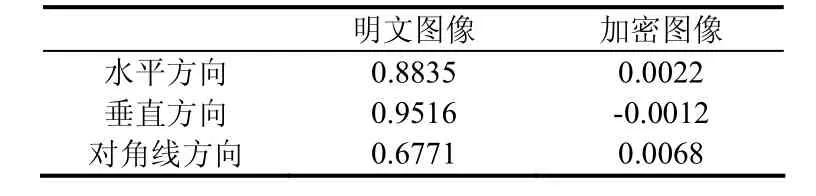
表1 两种图像中两相邻像素的相关系数

5 结语

文章提出了一种基于穷尽熵优化的混沌图像加密方案。通过利用穷尽熵来度量序列的类随机性强弱，选择熵最大的一组混沌序列对图像进行加密。最后，安全分析表明此加密方案具有对抗已知统计性攻击的鲁棒性。

[1]MATTHEWS R. One the Derivation of a Chaotic Encryption Algorithm[J]. Cryptologia, 1989(08):29-42.

[2]陈永红，黄席樾. 一种混沌系统的设计及其在图像保密变换中的应用[J].计算机应用, 2004,10（26）:52-55.

[3]唐林山，江成顺. 一种结合混沌的热流密码图像加密算法[J].计算机工程与应用,2007,43（03）:37-39.

[4]闵连权. 基于双置乱的图像加密算法[J].测绘科学, 2006,31（03）:71-73.

[5]FENG M. Analysis on Random-like Property of Chaotic Motions with Exhaustive Entropy[C]. Automation and Logistics, 2007 IEEE International Conference on, 2007: 2420-2425.

[6]KOHDA T, TSUNEDA A. Statistics of Chaotic Binary Sequences[J].IEEE Transactions on information theory,1997,43(11):104-112.

[7]SHANNON E. Communication Theory of Secrecy System[J]. J. Bell Syst. Tech., 1949(28):656-715.

[8]CHEN G R, MAO Y B, CHARLES K. A Symmetric Image Encryption Scheme based on 3D Chaotic Cat Maps[J]. Chaos, Solitons and Fractals, 2004(21):749-761.