粒子群优化的神经网络在齿轮故障诊断中的应用

2011-08-07张胜召齐金平陶海龙

铁路计算机应用 2011年12期

张胜召，齐金平，陶海龙

(兰州交通大学机电技术研究所，兰州730070)

随着铁路运输发展，为充分保证机车车辆安全运行，必须提高列车行走部件安全可靠性。齿轮作为机车传动的重要部件，其功能对安全运输起着举足轻重的作用，及时准确地发现齿轮的故障是保证生产安全运行的重要措施。因此, 对齿轮故障诊断理论和技术的研究具有重要的现实意义。

现代人工智能方法在故障诊断领域中已得到广泛的应用。其中人工神经网络具有非线性模式分类性能和很强的自组织、自学习能力，在齿轮故障诊断中得到了广泛应用。由于BP神经网络是沿梯度下降（平方误差函数）来进行搜索，存在收敛速度慢和容易陷入极小问题，因此需要对BP神经网络进行优化[1]。

粒子群优化算法是Kennedy和Eberhart[2]受鸟群觅食行为的启发而提出的一种基于群体智能原理的优化算法,它不仅避免了BP 算法陷入局部最优解, 而且没有遗传算法的交叉和变异等复杂操作过程, 可以搜索到最优结果, 避免了在局部最优处停留[3]。本文将粒子群化算法（PSO）和BP神经网络相结合，利用粒子群优化算法代替BP算法中的梯度下降法来训练神经网络的权重和阈值，改善了神经网络诊断性能。这不仅弥补了BP 神经网络的不足，而且删除了冗余连接，提高了故障的模式识别能力。

1 BP神经网络及PSO算法原理

1.1 BP神经网络原理

BP（Back progation）网络是目前应用最为广泛的一种前馈网络，应用最广泛的神经网络模型之一。BP算法基本原理是梯度最速下降法，其中心思想是反复的调整权值，使其网络总误差最小，即采用梯度下降法来指导搜索，使其网络的实际输出值与期望输出值的误差均方值为最小。其拓扑结构由输入层、隐含层和输出层组成。在本文中神经网络优化模型采用3层BP网络，输入层，中间层（隐含层）和输出层，其网络结构如图1。

1.2 PSO算法原理 [4]

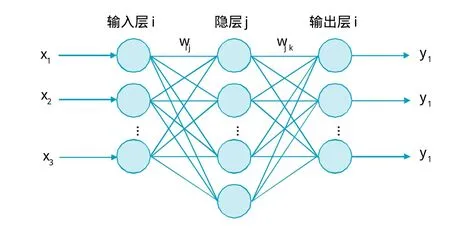
图1 BP网络结构

PSO初始化为一群随机粒子（即随机解），每个优化问题的潜在解都是搜索空间的粒子，每个粒子还有一个速度向量决定他们飞行的方向和距离，所有的粒子都有一个被优化的函数决定的适应值，然后粒子们就追随当前的最优粒子在解空间中搜索，通过迭代找到最优解。

假设在一个D维的搜索空间中第i个粒子位置和速度分别为Xi=（xi1xi2… xid）和Vi=（vi1vi2… vid），在每一次迭代中，每个粒子通过跟踪两个“最好位置”来更新自己，一个是粒子本身目前所找到的最好位置，即个体极值pbi=（pbi1pbi2…pbiD），另一个是目前整个群体中所有粒子发现的最好位置，即全局极值gb=(gb1gb2… gbD)，gb是在pb中的最好值。对于第k次迭代，每个粒子是按照式(1)和式(2)进行变化的。

公式中：i=1,2…m,m是该群体中粒子总数；d=1,2…，D；为第k次迭代粒子i飞行速度矢量的第d维分量;为第k次迭代粒子i位置矢量的第d 维分量；pid为粒子i个体最好位置pbest 的第d维分量; pgd为粒子群体最好位置gbest 的第d维分量; 学习因子c1和c2是非负常数； rand( )是介于[0,1] 之间的随机数；惯性权重w为非负数，文献[5] 提出了式（1）中惯性权重w的自适应改变惯性权重的线性变化公式：

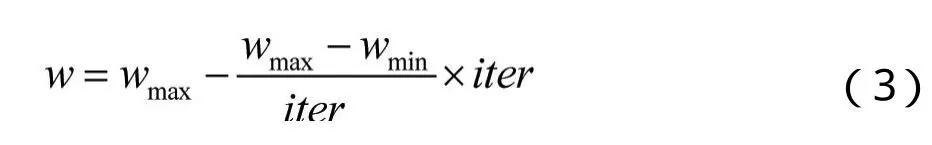
式(3)中：wmax、wmin为惯性权重的最大值和最小值；itermax、iter为当前迭代次数和最大迭代次数。

2 基于PSO 神经网络的故障诊断方法

粒子群优化BP神经网络是在网络反向传播过程中，通过各个粒子在其搜索空间内搜索各层间连接权值和阈值, 粒子群在各个粒子搜索时, 迭代公式简单计算速度比梯度下降法快得多, 通过惯性权重函数w的调整很好的跳出局部极小值。设置粒子的适应值函数，在本文中选用均方差作为BP神经网络的适应值函数。

式（4）中N是训练集的样本数；ydj,i是第i个样本的第j个网络输出节点的理想输出值；yj,i是第i个样本的第j个网络输出节点的实际输出值；C是网络输出神经元的个数。

基于PSO -BP网络故障诊断流程如下[6]：

（1）初始化BP网络结构，设定网络的输入层、隐含层、输出层的神经元个数；按照式（1）和（2）初始化粒子的初始位置x0id及其速度v0id，确定粒子的个数m、惯性权重w的初值、最大迭代次数itermax、学习因子c1和c2。

（2）根据BP 网络算法计算出每个粒子相应个体极值的适应度值，而全局极值就是个体极值中最好的, 再将gbd(整个粒子群在第d 维的全局极值点的位置)设置为该最好粒子的当前位置。

（3）评价和计算出每一个粒子的适应度值J,若好于该粒子当前的个体极值, 则将pbd（当前最优位置）设置为该粒子的位置, 并更新个体极值。若所有粒子的个体极值中最好的好于当前的全局极值,则将gb设置为该粒子的位置。并更新全局极值。

（4）按式（1）～式（4）对每一个粒子的位置和速度进行更新，并考虑更新后的位置和速度是否在有限的范围内。

（5）检验是否符合结束条件。若最大迭代次数或当前位置达到预定的误差要求, 则停止迭代，输出最后一次迭代的结果即为所求的全局最优的权值和阈值, 否则就转到（2），继续迭代直到算法收敛。

3 齿轮故障诊断实验

选取某机车发动机齿轮箱的齿轮故障的15个特征参数，这15个参数组成输入样本，实测数据经归一化处理后如表1。

（1）以表1中13组数据中选取10组(序号1-10)作为BP神经网络输入样本；

表1 齿轮箱状态样本数据

（2）对输出状态进行编码，输出为三维向量，定义期望输出向量如表2。

表2 齿轮箱状态编码对照表

（3）构建BP神经网络，网络参数如下表3。

应用输入样本和输出样本向量对网络进行训练，分别用带动量的BP和PSO-BP网络对所有10个样本进行检验，网络误差曲线分别如图2和图3。

表3 网络参数

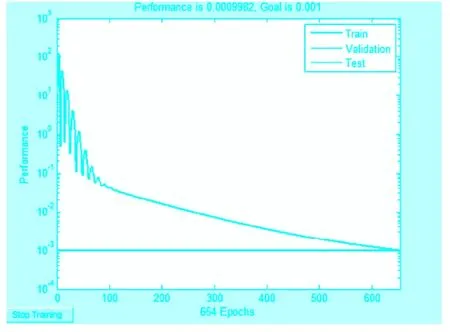
图2 带动量的BP网络

图3 PSO-BP网络

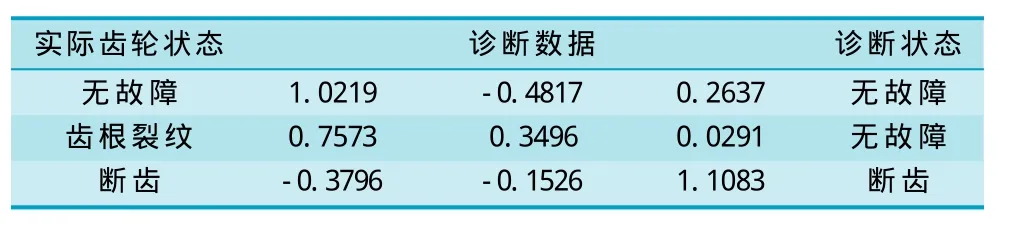
表4 带动量的BP网络诊断结果

表5 PSO-BP网络诊断结果

表4为带动量BP网络诊断结果，表5为基于PSO算法BP网络诊断结果，说明相对于带动量BP网络（精度为66.7%），基于PSO算法BP网络具有更高的诊断精度（精度为100%）。从图2中可知网络需迭代654次收敛到误差精度，从图3中可知网络只需迭代128次收敛到误差精度。故相对于带动量的BP网络，基于改进PSO算法的BP网络不但具有更好的故障诊断精度，并且提高了网络的收敛速度。