刷密封刷丝力学行为与密封性能

王之栎 郭苗苗 李理科

(北京航空航天大学 机械工程及自动化学院，北京100191)

刷密封中刷丝的变形能消除或减小由转子径向跳动等引起的密封间隙，因此被应用于发动机旋转件间的动密封，相对迷宫密封，其泄漏率可下降至后者的1/2～1/5，使推力/油耗比上升.刷丝尖端在转子表面滑动，刷丝的力学行为以及接触过程中产生的摩擦等是影响密封性能的主要因素.文献［1］对刷密封中转子与密封刷接触扭矩进行了实验测试;文献［2］建立了刷丝变形的力学模型以及针对刷密封的磨损建模分析;文献［3］就刷丝间摩擦力分布对滞后的影响以及转子与刷丝间接触力进行了研究分析;文献［4］建立了基于CFD多孔介质刷密封模型，在此基础上对刷丝轴向和周向两个方向的变形进行了研究.本文将对刷密封压场和流场作用下的刷丝力学系统建立有限元模型，进而分析刷丝力学行为对密封性能的影响.

1 刷密封模型及实验装置

刷密封由紧密排列的金属刷丝和用于固定刷丝束的前板和背板组成，刷丝在周向平面内与转子径向呈一定倾角轴对称排列，如图1a和图1b所示.图1c为设计有长前板结构与背板低滞后结构的密封形式［5－6］.刷丝区域前的长前板，可以减小高压气体对前排刷丝的扰动，保持了其径向压紧“blow down”状态，密封能力得以维持.当刷丝被压紧时，将导致刷丝束间摩擦增大，柔性降低，跟随性下降，尤其当转子偏心运转或瞬时侵入刷丝束并回复初始状态时，刷丝不能立即随之恢复与轴的贴紧状态，而发生“hang up”，称为滞后效应.图1c所示背板低滞后结构可以有效减缓滞后效应的发生.根据密封刷环的特性，创建刷密封实验台如图2所示.

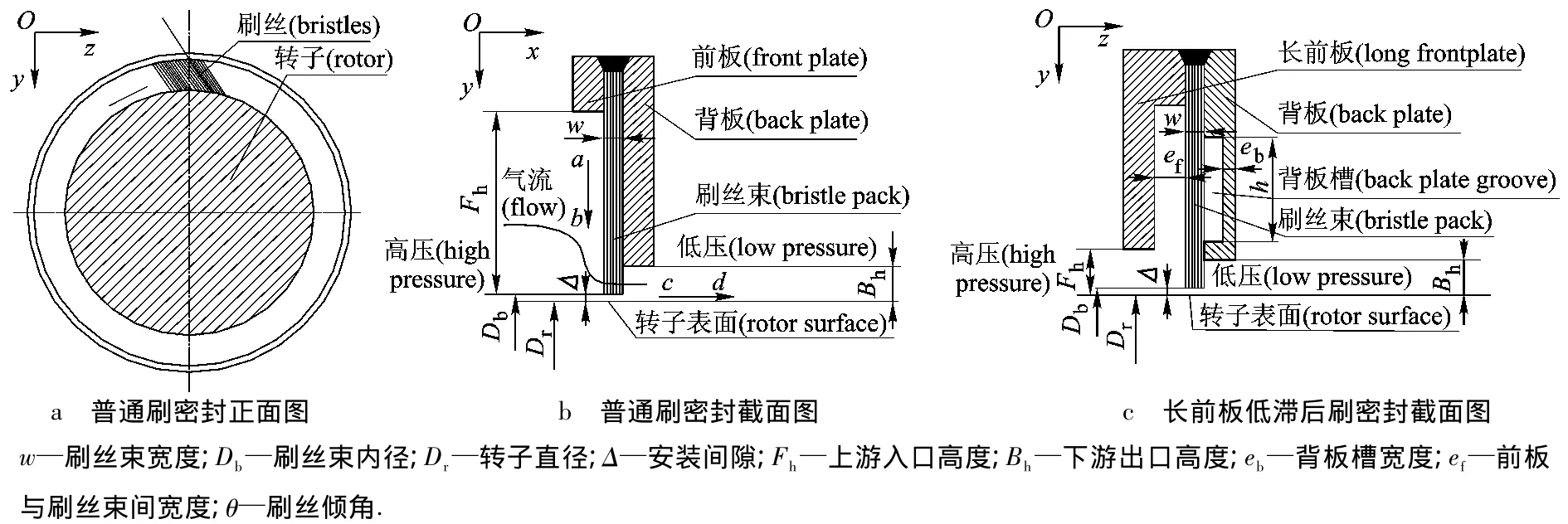
图1 刷密封几何结构图

图2 刷密封实验台

2 刷密封设计分析计算模型

2.1 流场计算模型与算法

刷密封压力场的研究是研究刷丝力学行为的基础.由于密封具有轴对称结构，截取二维计算区域如图3所示，采用自主开发的刷密封软件Field CAL(以下简称Field CAL)借助多孔介质模型，引入各向异性的阻抗力来表示刷丝区域对流体的阻抗作用，将流体的控制方程组在流场区域离散，应用“修正的解压力耦合方程的半隐式算法”——SIMPLER算法迭代求解［7］.计算流场的控制方程组为

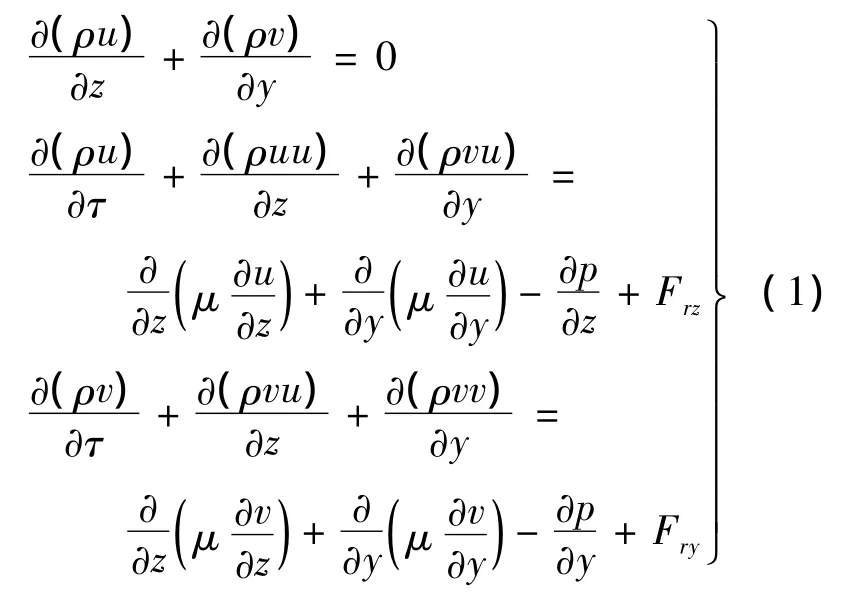
式(1)由质量守恒方程和动量守恒方程构成.其中，ρ为气体密度;u，v分别为x轴和y轴方向气流速度;τ为时间;μ为气体粘度;p为气体压力;单位体积内刷丝对流体的阻抗力［8］为

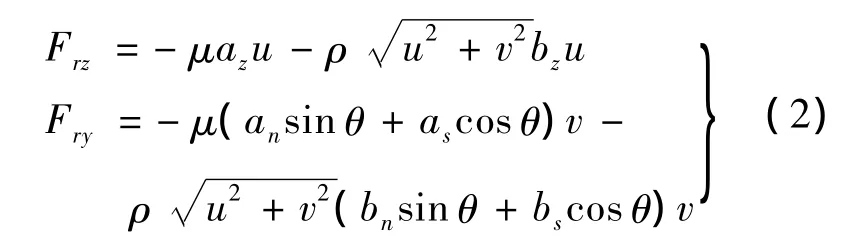
其中，az，an和 as分别为沿 z轴方向、x-y平面内垂直刷丝方向和沿刷丝方向的粘性阻抗系数;bz，bn，bs分别为相应方向上的惯性阻抗系数.无刷丝区域流场的阻抗系数为0.

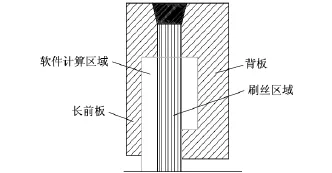
图3 刷密封计算区域

计算密封区域压力值后，根据刷丝在流场中的初始位置，可分别得到x-y平面和y-z平面内单根刷丝各节点x向和y向压差及流场对刷丝的作用力.

2.2 刷丝有限元模型

考虑压力对刷丝作用、刷丝和转子之间接触力、刷丝之间以及刷丝与背板之间作用力，采用悬臂梁理论对系统进行有限元求解，计算出刷丝受力和变形及转子所受摩擦扭矩.

2.2.1 刷丝受力分析

在周向-径向平面内以刷丝固定端为原点建立y轴、z轴;转子轴线方向为x轴.刷丝与y轴呈一定倾角θ在圆周内对称安装.x-y平面内气体从高压侧流向低压侧.

x-y平面和y-z平面内刷丝受力如图4a、图4b所示.为便于刷丝受力与变形分析，在图4a中刷丝局部以其固定端为坐标原点、刷丝轴向为s轴、垂直刷丝轴向为t轴建立辅助直角坐标系.平面内刷丝端部与转子表面接触力F=f(Ff，Fn)，刷丝在流场中所受的气体压力Δqp由流场确定，刷丝之间存在相互作用力fi，图4b中最后一排刷丝还受到背板作用力fb.

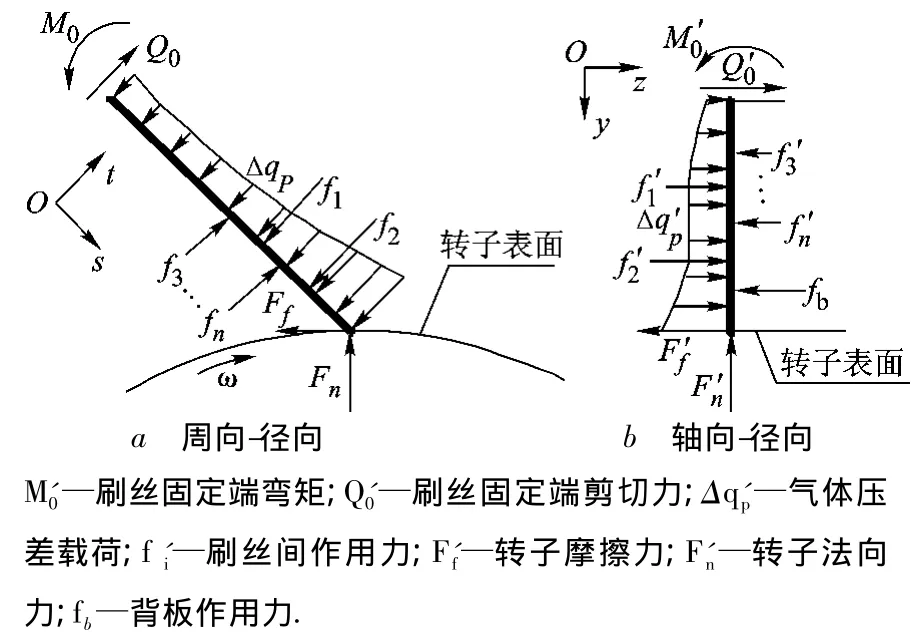
图4 刷丝受力模型

2.2.2 刷丝有限元模型建立

根据刷丝受力和变形特点，将单根刷丝视为悬臂梁采用有限元法进行计算.

在图4a中弯曲梁单元变形遵守伯努利-欧拉法则，有

其中，E为刷丝弹性模量;I为惯性矩;M为单元所受弯矩.

由悬臂梁弯曲理论可得未加载流场时由过盈安装导致的刷丝端部法向力:

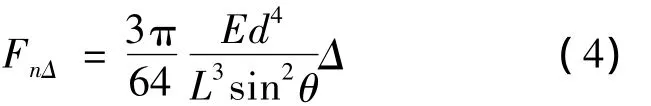
其中，d为刷丝直径;L为刷丝自由长;Δ为过盈量;E为刷丝弹性模量.

在有限元模型中，每一根刷丝被分成k个小单元，因而在单元le内，可将流场压差视为均布载荷qe，得到流场中空气动力产生的单元载荷矩阵:

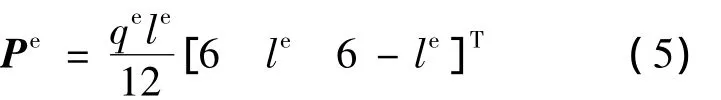
刷丝单元刚度矩阵:

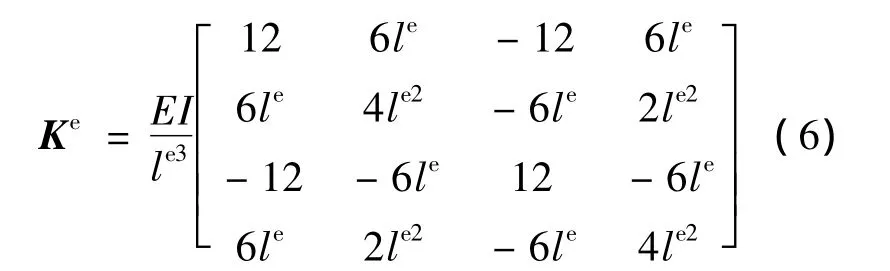
综合考虑刷丝与转子接触力和压力，根据表征单元应变和位移关系的几何方程、应力应变关系对应的物理方程可列出平衡方程，加载位移和力边界条件，得到平衡方程的解，从而计算出节点受力和变形值.

刷丝变形位移边界条件设定如下:

1)刷丝固定端节点横向变形量.

2)刷丝端部节点横向变形量.

由于刷丝变形为小变形，可认为刷丝端部平衡位置即为初始接触位置，因此，刷丝与转子间隙安装条件下:

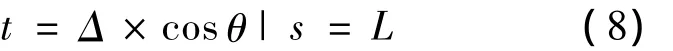
过盈安装条件下:

t0为初装时(未加载流场)刷丝端部变形量.

另外，在y-z平面内计算刷丝变形时，位移边界条件包括:刷丝固定端边界;各排刷丝之间以及最后一排刷丝与背板之间存在最大允许位移.

3 计算结果及其分析

3.1 参数设置

刷密封设计分析软件及实验的刷密封结构参数和主要工况参数设置如表1所示.

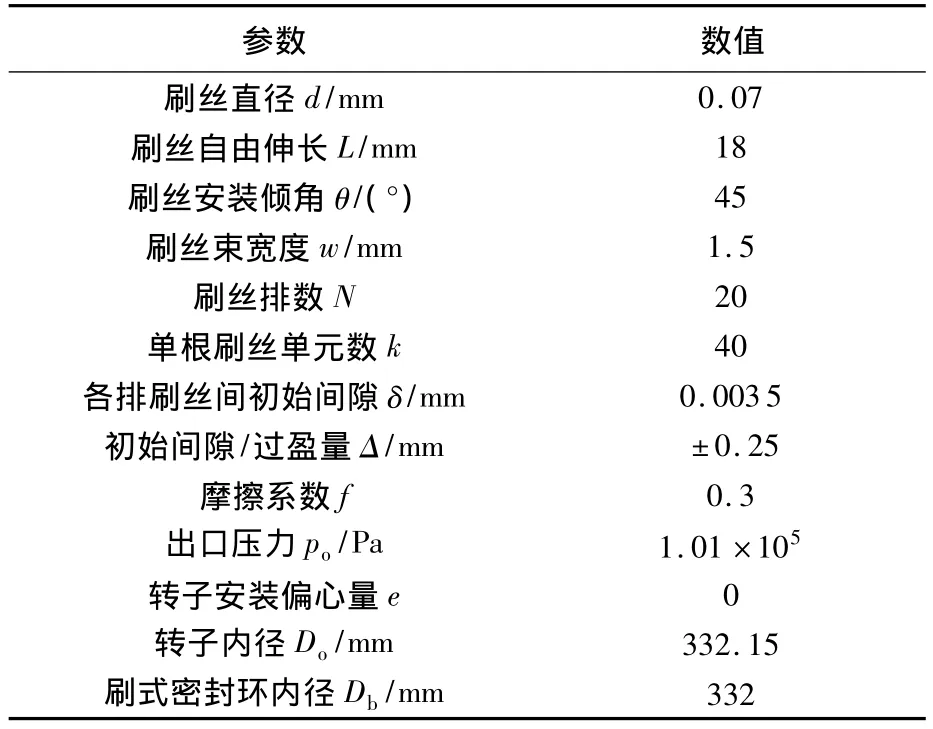
表1 刷密封主要计算参数

3.2 压力场分布

刷密封中压力场，y-z平面即轴向-径向平面内密封区域压力分布见图5，该区域内y轴和z轴方向分别存在径向和轴向压力梯度，下游出口处压力梯度最大.背板槽中产生均布的压力，避免高压下的刷丝束紧密贴紧背板而导致跟随性下降.由于x-y平面压力分布视为轴对称，因而根据图5可得压比1.5时x-y平面内压力分布.

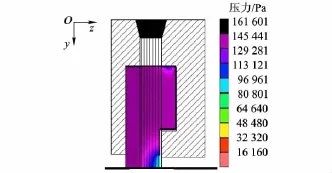
图5 压力场分布

3.3 刷丝变形

在得到压力分布之后，就可以计算出压力场中刷丝的变形情况.刷丝从高压入口端到低压出口端依次排列为第1排～第20排.

3.3.1 刷丝轴向-径向变形

图6为进出口压比为1.5，安装过盈量为0.075 mm的轴向-径向变形图.

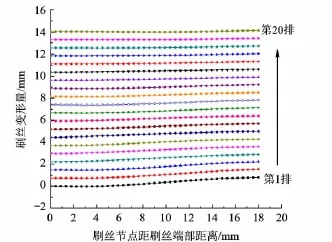
图6 刷丝轴向-径向变形

刷丝自由端在压力梯度作用下变形较大，而最后一排受到背板的限制变形量相对较小.在轴向压力的作用下，刷丝束整体向背板贴近.

3.3.2 刷丝周向-径向的变形

安装过盈量0.075 mm，进出口压比1.5时的周向-径向变形如图7所示，由于初装径向弹力的作用下，刷丝束将沿径向向外弯曲变形.在转子旋转时，刷丝受到转子表面摩擦力Ff和法向弹力Fn与流体压力共同作用，从而使刷丝端部贴近转子，达到平衡状态.间隙安装的周向-径向刷丝变形如图8所示，进出口压比 1.5，安装间隙为0.25 mm.

因压场中靠近出口处的径向压降相对较大，后排刷丝变形大于前排，即较大的压力降使得刷丝更贴近转子以减小或闭合密封刷环初始安装的间隙并减小泄漏量.

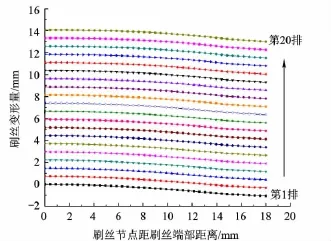
图7 刷丝周向-径向变形(过盈安装)

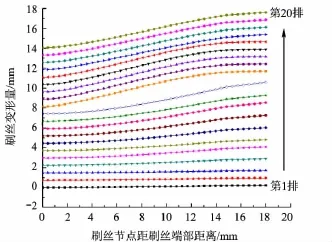
图8 刷丝周向-径向变形(间隙安装)

比较图7和图8周向-径向变形可知，间隙和过盈2种不同安装形式下受刷丝与转子间弹力与压场径向压降共同作用下的刷丝变形达到平衡;受轴向流场的影响，间隙安装时下游刷丝变形比上游的明显偏大，上游可能形成缝隙;而过盈安装时上下游各排刷丝变形接近，端部节点位移即为初装位移量，此时刷丝端部均与转子表面接触.

3.4 性能分析

3.4.1 泄 漏 量

保持稳定的低泄漏量是密封性能的重要评判标准之一.基于Field CAL的计算结果与实验结果比较如图9所示.

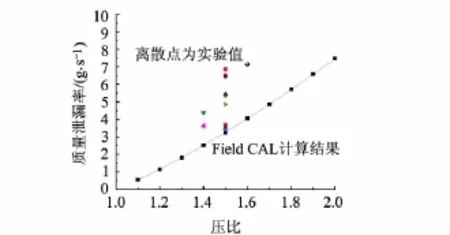
图9 小压比情况下的泄漏率对比

其中压比范围是1.1～2.0.相同压比情况下的实验值比程序值相对较大.Field CAL中使用阻抗力来代替真实刷丝对气体的阻碍作用，阻抗系数取自文献［4］.实际上密封刷中的刷丝束排列有的地方紧密有的地方稀疏，需综合考虑阻抗系数的取值.

3.4.2 摩擦扭矩

摩擦扭矩是刷密封数值计算和实验测量的关键参数.基于流场中刷丝受力的计算，使用Field CAL可以计算出不同安装状态与不同工况下的摩擦扭矩.

图10为Field CAL计算得出不同压差，不同安装过盈量下的刷丝端部与转子之间摩擦扭矩值.摩擦扭矩随着安装过盈量的增大和压差的增大而增大.表明压力增大，压力降使得刷丝更加紧密地贴近转子，因而摩擦扭矩会随之增大.

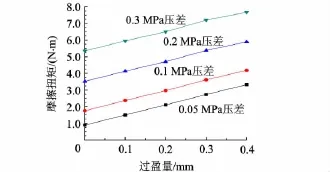
图10 摩擦扭矩与过盈量关系曲线

图11为实验测试与Field CAL计算，没有加压力情况下不同转速对应的摩擦扭矩曲线对比，表明转子低转速变化时与摩擦扭矩关系不大.

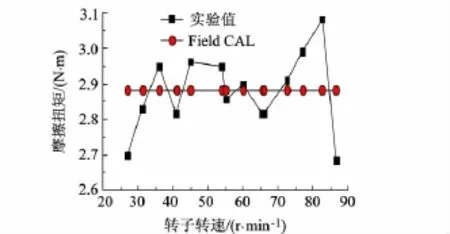
图11 摩擦扭矩与转子转速关系曲线

4 结论

刷密封中流场分布和刷环与转子安装过盈量是影响刷丝系统力学响应的关键因素.基于Field CAL计算的压力场对刷丝受力与变形的计算，得到轴向-径向和周向-径向2个方向的刷丝变形量，并在此基础上得到安装过盈量和密封压差与摩擦扭矩的关系.主要结论如下:

1)影响刷丝轴向-径向平面内受力和变形的主要因素是流场的作用，且由于靠近转子压力梯度较大，刷丝变形量较大;而背板的支撑作用使前排刷丝的变形量大于后排;

2)周向-径向平面内刷丝行为与安装形式有关.过盈安装时，刷丝端部与转子之间接触力的作用使得刷丝弯曲变形;间隙安装时，压力梯度会使得刷丝贴近转子使间隙闭合或减小;

3)作为刷密封实验测量的主要参数之一，刷丝端部摩擦扭矩与安装过盈量及密封两侧压差均基本呈递增关系，在刷密封设计中对于这些参量应予控制，低转速时，摩擦扭矩与转子转速关系不大;

4)Field CAL中阻抗系数的选取是能否准确模拟刷密封压场与流场并计算其性能参数的关键因素之一.小压比情况下的泄漏量的实验测试值与Field CAL计算值的比较分析，为该工况下的阻抗系数选取和程序的修正提供了可靠的依据.

References)

［1］Wood P E，Jones T V.A test facility for the measurement of torques at the shaft to seal interface in brush seals［J］.Journal of Engineering for Gas Turbines and Power，1999，121(1):160 －166

［2］Aksit M F，Tichy J A.Wear of brush seals:background and new modeling approach［J］.Tribol.Trans.，1998，41(3):368 － 374

［3］Zhao H，Stango R J.Role of distributed interbristle friction force on brush seal hysteresis［J］.ASME Journal of Tribology，2007，129:199－204

［4］Chew J W，Lapworth B L，Millener P J.Mathematical modeling of brush seals［J］.Int.J.Heat Fluid Flow，1995，16(6):493 －500

［5］Yahya Dogu，Aksit M F.Effects of geometry on brush seal pressure and flow fields—part I:front plate configurations［J］.Journal of Turbomachinery，2006，128:367 －378

［6］Yahya Dogu，Aksit M F.Effects of geometry on brush seal pressure and flow flieds—part II:backing plate configurations［J］.Journal of Turbomachinery，2006，128:379 －389

［7］王之栎，梁小峰，宋飞，等.低滞后刷式密封数值分析［J］.北京航空航天大学学报，2008，34(9):1080－1083 Wang Zhili，Liang Xiaofeng，Song Fei，et al.Low hysteresis brush seal numerical situmulations［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(9):1080 － 1083(in Chinese)

［8］王之栎，梁小峰，黄其武.刷式密封二维模型数值计算［J］.航空动力学报，2008，23(8):1461 －1465 Wang Zhili，Liang Xiaofeng，Huang Qiwu.Two-dimensional model mathematical stimulation of brush seals［J］.Journal of Aerospace Power，2008，23(8):1461 －145(in Chinese)