层次分析法在物流中心选址过程中的应用
2011-08-03吕叶
吕 叶
(西南交通大学交通运输与物流学院,成都 611756)
物流中心(logistics center)又称为流通中心,是组织、衔接、管理物流活动的据点。物流中心主要面向社会服务,拥有健全的物流功能,完善的信息网络,辐射范围大,储存、吞吐能力强。因此,在一个具有若干需求网点和与之相配套的经济区域内,选一个地理位置设置物流中心,便是我们关注的话题。较成功的物流中心选址方案能够使商品的流通全过程的效益达到最优。物流中心集中了流通领域的多种物流功能,是组织物流作业和调节物流供需的基地,如果选址不佳,将产生极大的负面影响。
1 物流中心地址的选择
1.1 物流中心选址的原则
物流中心位置的选择有多种方法,包括定性分析和定量计算两类。无论采用何种理论方法进行物流中心的选址,首先要遵守适应性、协调性、经济性和战略性四项原则。
具体来说,物流中心的选址须与国家、省市的经济发展方针、政策相适应,与我国的物流资源供给和需求分布相适应,以符合适应性原则;物流中心的选址应将国家的物流网络作为一个大系统来考虑,使物流中心的设施设备在地域分布、物流作业生产力和技术水平等方面互相协调,以符合协调性原则;物流中心的选址应满足费用(包括建设费用和经营费用)最低,以符合经济性原则;物流中心的选址应具有战略眼光,既要考虑日前需要,又要考虑长远发展,以符合战略性原则。
1.2 物流中心选址的影响因素
随着现代物流学的发展和成熟,人们已取得共识,物流中心的选址应考虑以下因素。
(1)自然环境因素,包括气象条件、地质条件、水文条件和地形条件。
(2)经营环境因素,包括物流中心所在地的优惠物流产业政策,劳动力保障能力,对商品特性的要求,物流费用情况以及服务水平。
(3)基础设施状况,包括物流中心所在地的交通条件以及公共设施状况。
(4)其他因素,包括物流中心所在地的国土资源利用情况,环境保护要求和周边工业生产状况。
1.3 物流中心选址的方法概述
物流中心的选址在综合考虑基本原则和影响因素的前提下,可以用以下方法选择位置。
(1)坐标分析法[3]。在一个地域范围,如果若干用户位置已确定,同时可以掌握用户平均需求量,则可选择用总费用最低的地方为流通中心最优位置,可先将用户位置置于坐标图上,各用户坐标为xiyi(i=1,2,3…n,设有n个用户),各用户的需要量为wi(i=1,2,3…n)。最优的配送中心地理位置x0y0应当是xiyi(i=1,2,3…n)这n个用户与x0y0直线距离li乘以相应用户的需要量wi,再乘以配送费用率k,求和值为最小,即的地点。(2)求解运输模型法。该方法是指采取数学模型并求解的方法确定物流中心位置。例如,利用线性规划方法,在多种条件约束下,建立数学模型,使物流中心的投资额、运营成本、货物运输总费用达到最小。(3)方案比较法。在已建满了多种建筑物的城市中可能只有有限的几处地址可供修建物流中心,在这种情况下,可采用方案比较法。方案比较法以每一个可能建立物流中心的选址处所为一种方案,方案过多时,可以先用直观判断方法进行一次筛选,将明显不利的方案除去,保留少数有价值的方案。接下来再对各保留方案进行评估,确定最优方案。在方案评估的具体过程中,有多种操作方法,现应用层次分析法对物流中心的选址方案进行评估。
2 层次分析法在物流中心选址中的应用
2.1 层次分析法概述
许多评价问题的评价对象属性多样,结构复杂,难以完全采用定量方法评价,也难以做到评价项目具有单一层次结构。这时需要首先建立多要素、多层次的评价系统,并采用定性与定量相结合的方法,使复杂的评价问题明朗化。在这样的情况下,美国运筹学家,匹兹堡大学教授 T.L.萨迪(T.L.Satty)于20世纪70年代提出了著名的AHP方法(Analytic Hierarchy Process,解析递阶过程,通常译为“层次分析”法)。
2.2 层次分析法的基本思想和实施步骤
层次分析法(AHP)把复杂的问题分解成各个组成因素,对这些因素按支配关系分组形成递阶层次结构。通过两两比较的方式确定层次中各因素的相对重要性,然后综合有关人员的判断,确定备选方案的相对重要性的总排序。
在应用层次分析法进行方案评估时,大体可分为4个步骤。
(1)分析评价系统中各基本要素之间的关系,建立系统的递阶层次结构。递阶层次结构一般分为3层,最高层为目标层,这一层次中只有一个要素,一般是分析问题的预定目标;第二层为准则层,这一层次包括了为实现目标所涉及的中间环节,可以由若干个层次组成,即可以存在与准则层产生关联,受准则层各要素支配的子准则层;第三层为方案层,表示为实现目标可供选择的各种方案、措施等。各层次结构示意如图1所示。

图1 层次分析法结构模型
(2)对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较判断矩阵,并进行一致性检验。
(3)由判断矩阵计算被比较要素对于该准则的相对权重。
(4)计算各层要素相对系统总目标的合成权重,并对各备选方案排序。
2.3 以物流中心选址方案为模型的层次分析法应用
(1)构建系统的递阶层次结构模型
物流中心选址方案的层次分析法评估的递阶层次模型中,目标层为“选择最优的物流中心地址”,准则层为“决定物流中心选址的影响因素”,如前文所述,包括自然环境因素、经营环境因素、基础设施状况以及其他因素,在影响因素的限定下,选择物流中心的建造地址,还应考虑以下因素:物流中心吞吐量、物流中心占地面积、物流中心结构形式与物流中心的技术装备等,这些因素可以构造为受准则层各要素支配的子准则层,子准则层各要素与准则层各要素之间具有可传递性和功能依存性。考虑到应用层次分析法评估物流中心选址方案的流程中,不同层次之间要素相对权重计算原理的相似性,这里做出如下假设:方案层中的选址方案的确定,只受准则层中各要素(限定在自然环境因素、经营环境因素、基础设施状况这3个方面)的影响,而忽略子准则层中各要素的影响,并且,选址方案限定在C1、C2、C33个方案,通过层次分析法得到最优方案。
评估物流中心的选址方案层次结构如图2所示。(2)建立各阶层的判断矩阵A,计算要素相对权重W以及进行一致性检验

图2 评估物流中心的选址方案层次结构
①建立各阶层的判断矩阵A

式中aij——表示一阶层中要素i与要素j对于上一阶层要素k的重要性标度。
标度定义见表1[4]。

表1 判断矩阵标度定义
②计算要素相对权重W
求各要素相对于上层某要素(准则等)的归一化相对重要度向量Wi常用方法为
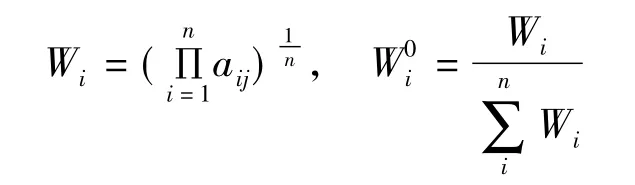
相对要素权重Wi,现实意义上即是比较一阶层上的各要素相对于上一阶层中某一要素归一化处理后所占优势的程度,权重越大,越占优势。
③一致性检验方法
第一步:计算一致性指标C.I.

第二步:查找相应的平均随机一致性指标R.I.(Random Index),1~12阶正互反矩阵计算1 000次得到的平均随机一致性指标如表2[4]所示。

表2 1~12阶正互反矩阵的平均随机一致性指标
第三步:计算一致性比例C.R.(Consistency Ratio)

C.R.的值应小于0.1才能通过一致性检验。
(3)通过对方案层C层要素相对权重的计算和排序来确定最优方案
以物流中心选址的评估为例,若准则层中各要素B1,B2,B3相对于目标层的要素A的权重为W1,W2,W3。方案层中,要素C1,C2,C3相对于准则层中的要素B1的权重为W11,W21,W31,相对于B2的权重为W12,W22,W32,相对于B3的权重为W13,W23,W33,如表3所示。

表3 方案总重要度计算
如表3所示,方案层中C1,C2,C3的权重,最后通过筛选出最大的,则最优方案为Ci。
(4)层次分析法在物流中心选址过程中的应用实例
对于物流中心选址时,应用层次分析法所涉及到的层次结构模型中各层次中要素的重要性标度的确定,进行下列假设:相对于目标层要素A,准则层中,并且对于方案层中的3种方案C1,C2,C3,相对于准则层各要素来说,对于自然环境因素B1,3种方案优劣排序为C1>C2>C3,对于经营环境因素B2,3种方案优劣排序为C2>C3>C1,对于基础设施状况B3,3种方案优劣排序为C3>C2=C1。
C1,C2,C3相对于上一阶层中每一要素的重要性标度,将体现在下面的计算列表当中。
由表4可得:λmax≈3.009

表4 准则层各要素相对目的层要素的重要度统计
由表5可得:λmax≈3.004

表5 方案层各要素相对准则层要素一的重要度统计
由表6可得:λmax≈3.009

表6 方案层各要素相对准则层要素二的重要度统计
由表7可得:λmax≈3.000


表7 方案层各要素相对准则层要素三的重要度统计
对各方案的总重要度的计算结果表明(表8),3个选址方案的优劣顺序为C2(W2=0.403),C3(W3=0.329),C1(W1=0.268)。因此C2方案综合效果最好,作为入选方案。
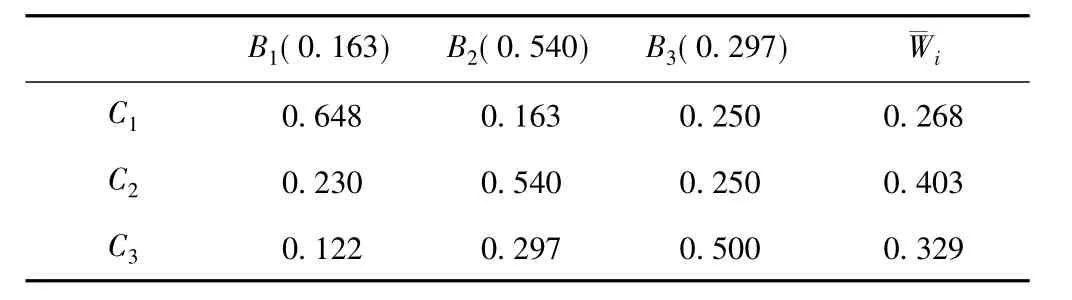
表8 物流中心选址方案总重要度计算
3 结论
对于目前物流中心选址问题的讨论,在运用数学模型进行综合评价时,除了使用层次分析法(AHP法),也可以采用模糊综合评价法,还可以应用Hopfield人工神经网络。本文突出了层次分析法在物流中心选址过程中的应用,但是在实际应用中,对未来情况的考虑是不能被忽略的,因此,在物流中心选址方案的评价上,综合未来因素的动态评价是非常有研究价值的。
除此之外,在对物流中心选址问题的探讨上,还应注意的是,单独的物流中心作用范围有限,对于大范围的经济区域来讲,选择合适的场站,形成物流中心网络,并进行合理布局,可以发挥更大的作用。
[1]何明珂.现代物流配送中心:推动流通创新的趋势[M].北京:中国商业出版社,1997.He Mingke.Modern Logistics Distribution Center∶Pushing Forward the Trend of Creation in Areas of Logistics[M]Beijing∶China Commerce Press,1997.
[2]徐杰,郑凯,田源,汝宜红.物流中心选址的影响因素分析及案例[J].北方交通大学学报,2001(10):80-82.Xu Jie,Zhengkai,Tian Yuan,Ru Yihong.Research of Logistics Center Location and Case Analysis[J].Journal of Northern Jiaotong University,2001(10):80-82。
[3]叶怀珍.现代物流学[M].北京:高等教育出版社,2006.Ye Huaizhen.Modern Logistics[M].Beijing:Higher Education Press,2006.
[4]汪应洛.系统工程[M].北京:机械工业出版社,2008.Wang Yingluo.Systems Engineering[M].Beijing:China Machine Press,2008.
[5]王健,余政峰.物流中心选址的动态评价方法研究[J].公路交通科技,2007(10):147-149.Wang Jian,Yu Zhengfeng.Research on Dynamic Evaluation Method ofLogistic Center Location[J].JournalofHighway and Transportation Research and Development,2007(10):147-149.
[6]张艳霞,马丽娟.物流中心选址问题研究现状[J].商业研究,2005(10):157-159.Zhang Yanxia,Ma Lijuan.Research Situation about Logistic Center Location[J].Commercial Research,2005(10):157-159.
[7]黄才骏.中国铁路物资流通[M].北京:中国铁道出版社,1996.Huang Caijun.China Railway Resources Circulation[M].Beijing:China Raiway Publishing House,1996.
[8]谭跃进,陈英武,易进先.系统工程原理[M].长沙:国防科技大学出版社,1999.Tan Yuejin,Chen Yingwu,Yi Jinxian.Principle of Systems Engineering[M].Changsha:Press of National University of Defense Technology,1999.
