公路隧道出入口平面线形一致性检验研究

庞小冲，唐学军

(甘肃省交通规划勘察设计院有限责任公司，兰州 730030)

0 引言

随着公路建设向山区、城市等复杂的地形、地物地区发展，项目选线中隧道洞口段位于回旋曲线上并不少见，由于隧道结构的特殊性，考虑到洞口段行车的安全，相关的规范对隧道出入口的平面线形有专门的要求，以提高进出隧道的安全性［1］。现行规范中，对隧道出入口的平面线形一致性的规定主要有3处，依据规范实施的时间顺序依次介绍如下。

首先，JTG B01—2003《公路工程技术标准》第7．0．4条对隧道洞口线形规定:“隧道洞口内侧不小于3 s设计速度行程长度与洞口外侧不小于3 s设计速度行程长度范围内的平、纵线形应一致［2］”。

其次，JTGD70—2004《公路隧道设计规范》第

4．3．5条规定:“隧道洞外连接线应与隧道线形相协调，并符合隧道洞口内外各3 s设计速度行程长度范围的平面线形应一致［3］”。可见，与前一规范的要求基本一致。

第三，JTG D20—2006《公路路线设计规范》第9．6．2条对隧道洞口线形规定:“平面线形不应有急骤的方向改变［4］”，但没有对“急骤的方向改变”作定量化的界定。

通常情况下，若隧道洞口内外各3s设计速度行程长度落在平曲线的圆曲线段或直线段范围内，则无疑被认为符合规范要求;但是，若隧道洞口内外各3 s设计速度行程长度落在缓和曲线段内，或者一部分落在缓和曲线段，一部分落在圆曲线段或直线段，则对于是否符合规范要求存在着不同的看法，也少见相关的技术人员对隧道洞口段线性的3 s要求作深入的分析研究。在具体的工作中往往为了保险起见，一般都按照不符合3s要求判断而不得不调整线位或者采用高指标，这样常常会增加工程的征地及土建费用。因此，本文旨在深入的探讨隧道洞口段线性的3 s要求的判定方法，即量化线形在满足安全性的条件下是否存在急骤变化。

1 平面线形一致性的判据研究

如前所述，3个规范中最晚实施的JTG D20—2006《公路路线设计规范》，对隧道洞口线形规定:“平面线形不应有急骤的方向改变”。假如，隧道出口是一个缓和曲线参数非常大的曲线，如R·Ls=2 000，这样的缓和曲线在一个较短的长度范围内，不妨就取3 s行程，可以看作是圆曲线，即驾驶员按照圆曲线行驶一段后，其位置与按缓和曲线行驶的位置的偏差很小，也即意味着平面线形没有急骤的改变。因此，首要问题是要对线形是否存在急骤改变确定一个定量化的标准。

JTG D20—2006《公路路线设计规范》第7．4．1 条规定了不设缓和曲线的圆曲线最小半径，再根据回旋曲线最小长度要求可以计算出相应的临界内移值p，如表1所示。

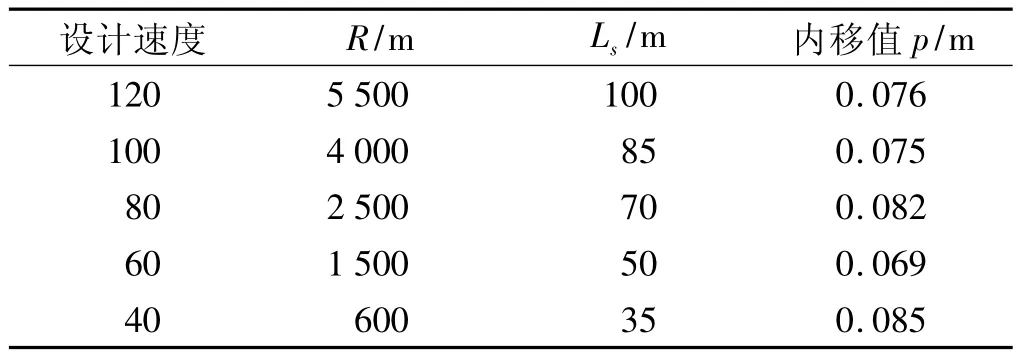
表1 曲线内移值参数Table 1 Parameters of critical inside movement value

以设计时速为80 km/h的隧道为例，相应的临界内移值p为0．08 m。如果在隧道洞口保持方向盘旋转角度不变，驾驶员继续按设计时速行驶3 s后的位置与行车道中心线的偏移值控制在0．08 m以内，那么就可以认为隧道入口平面线形没有急骤的改变。现以隧道洞口内外各3 s设计速度行程长度落在缓和曲线段为例，如图1所示。

图1 曲线一致性计算图式Fig．1 Sketch for curve consistency calculation

图中A，B，C 3点分别代表洞口位置、行车道中心线上距洞口3 s设计速度行程终点、驾驶员继续按设计时速行驶3 s后的位置。只要计算出B，C间的距离ΔD，并将ΔD与临界内移值p比较，若ΔD≤临界内移值p，可以认为隧道洞口内外各3 s设计速度行程长度范围的平面线形基本上保持一致;如果ΔD＞临界内移值p，则认为隧道洞口内外各3 s设计速度行程长度范围的平面线形没有保持一致。

2 主要算法

由图1看出:建立隧道出入口平面线形一致性检验判据的关键是要定出A，B，C 3点的坐标，这涉及到圆曲线、缓和曲线上任意点的坐标定点算法。为了适应特殊地形，有时需要在一个曲线上采用几个不同的半径形成复曲线，这在山区公路展线困难时经常遇到;因此，平曲线的坐标法定点算法应该能够考虑复曲线情况。

平曲线的各要素如图2所示。

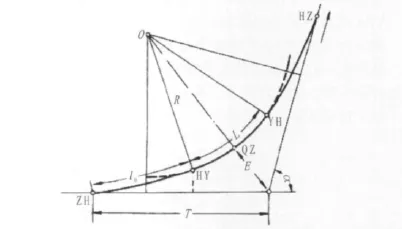
图2 标准缓和曲线要素图Fig．2 Sketch of elements of standard transition curve

2．1 曲线上任意点横距

只计算缓和曲线坐标时，需要用到一个中间变量——切线横距x，曲线上任意点的切线横距

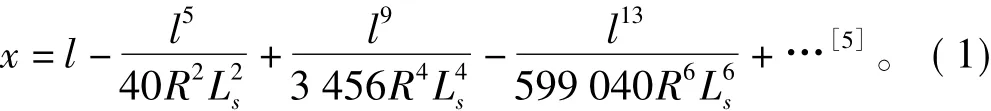
式中:l为缓和曲线上任意点至ZH(或HZ)点的曲线长;Ls为缓和曲线长度;R为圆曲线半径。

对于圆曲线两侧的缓和曲线不对称的复曲线，那么Ls和R值分别为所在缓和曲线的参数值，以下公式中同。

2．2 第一缓和曲线(ZH～HY)上任意点的坐标

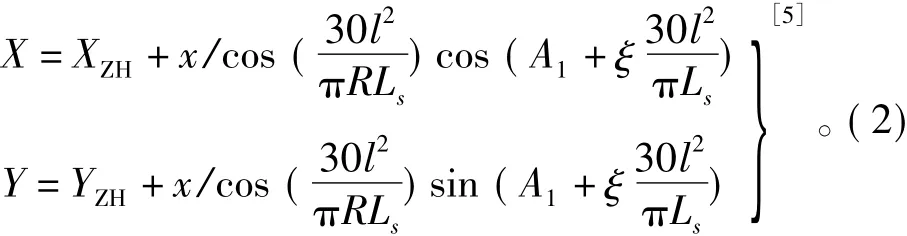
式中:l为圆曲线上任意点至HY点的曲线长;XZH，YZH为ZH点的坐标，可由相邻两交点的坐标及线路里程桩号求得;ξ为转角符号，右偏为“+”，左偏为“-”;Al为本交点与前交点连线的方位角。

2．3 圆曲线(HY～YH)上任意点的坐标

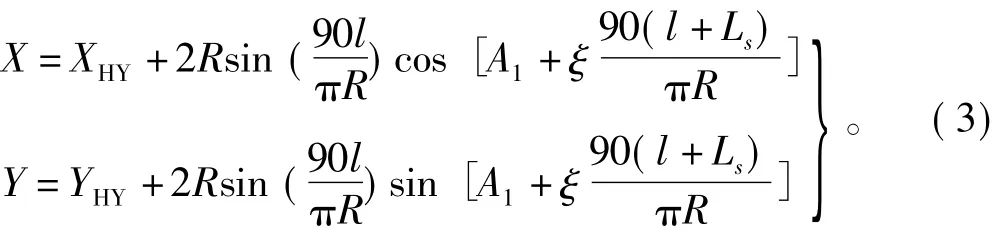
式中:l为圆曲线上任意点至YH点的曲线长;XHY，YHY为HY点的坐标，可由式(2)求得。

2．4 第二缓和曲线(YH～HZ)上任意点的坐标

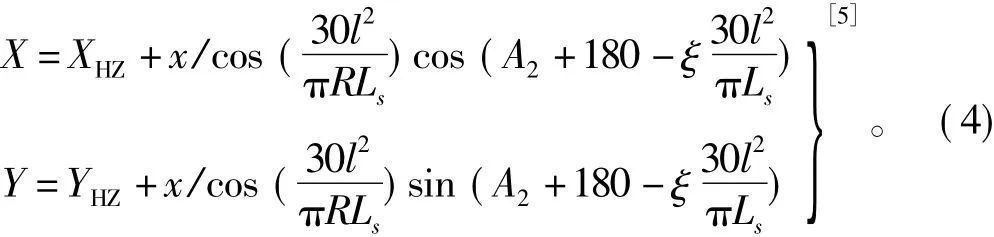
式中:l为第二缓和曲线上任意点至HZ点的曲线长;A2为本交点与后交点连线的方位角。

3 程序开发

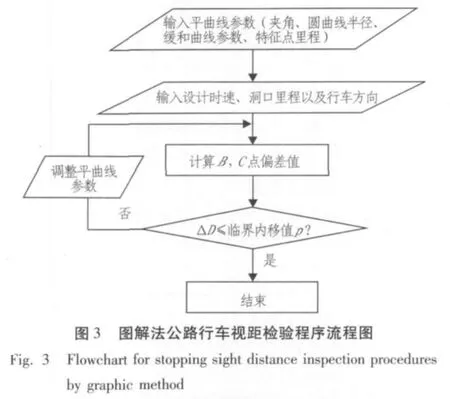
隧道出入口平面线形一致性检验的计算量很大，为此，作者在AutoCAD平台上采用2次开发方式和VBA语言开发了图解法公路行车视距检验程序。所谓2次开发就是利用某种开发语言，在软件商提供的基本功能上，为新增功能而做的开发工作，很多大型软件都提供2次开发接口。隧道出入口平面线形一致性检验程序的流程及检验对话框如图3和图4所示。

4 结论与建议

基于对相关规范关于隧道洞口平面线形一致性内容的深入对比和探讨，并通过量化计算分析，得到如下结论。

1)隧道洞口位于回旋曲线上时应严格按照量化判据来判定洞口段是否满足3 s要求，并提出了相关的计算方法。

2)提出了一个隧道出入口平面线形一致性的定量化判据，即行车道中心线上距洞口3 s设计速度行程终点与驾驶员继续按设计时速行驶3 s后的位置偏差ΔD≤临界内移值p，否则就认为不满足一致性要求。

3)针对隧道出入口平面线形一致性量化判据包括平曲线上缓和曲线、圆曲线上坐标的定点算法。计算较为复杂，工作量较大，本文在AutoCAD中利用二次开发方式开发了相关的程序，以获得直观高效的检验结果。

通过对目前高速公路设计中常见的隧道洞口段位于圆曲线和缓和曲线上的3 s要求进行分析探讨，对隧道洞口段的“3 s”安全提出了一个量化判据，对减小隧道洞口段的工程规模、征地拆迁等方面也有一定的积极意义;但隧道洞口段的行车安全还与洞口曲线段的视距、曲线的超高加宽以及视觉的“黑洞”、“白洞”效应有关，隧道洞口段行车安全受到多因素的制约，今后应对相关各因素做系统全面的分析探讨。

［1］ 徐家钰，程家驹．道路工程［M］．上海:同济大学出版社，1995．

［2］ 交通部公路司．JTG B01—2003公路工程技术标准［S］．北京:人民交通出版社，2003．(Department of Road Networks，Ministry of Transport of People’s Republic of China．JTG B01—2003 Technical standard of highway engineering［S］．Beijing:China Communications Press，2003．(in Chinese))

［3］ 重庆交通科研设计院．JTG D70—2004公路隧道设计规范［S］．北京:人民交通出版社，2004．(Chongqing Communications Research ＆ Design Institute．JTG D70—2004 Code for design of road tunnel［S］．Beijing:China Communications Press，2004．(in Chinese))

［4］ 中交第一公路勘察设计研究院．JTG D20—2006公路路线设计规范［S］．北京:人民交通出版社，2006．(CCCC First Highway Consultants Co．，Ltd．．JTG D20—2006 Design specification for highway alignment［S］．Beijing:China Communications Press，2006．(in Chinese))

［5］ 张雨化．道路勘测设计［M］．北京:人民交通出版社，2007．