一种适合求复数根的抛物牛顿割线法

黄志强，郭妞萍，王希云

(1.太原科技大学应用科学学院数学系，太原030024;2.西安财经学院统计学院，西安710061)

求解非线性方程f(x)=0根x*的数值方法首推牛顿迭代法[1]，其思想是给定一个初始近似解，过该点作曲线的切线，若切线与x轴相交，新近似解可采用该交点的横坐标，依此类推，得到—个近似解序列{xk}.迭代格式为:xn+1=xn-f(xn)·[f'(xn)]-1，n=1，2，…，但牛顿迭代法的一个明显缺点是对每一个k都要计算f'(xk)，导数的计算往往十分麻烦，尤其当f'(xk)相对较小时，计算要很精确，否则会产生很大的舍入误差。因此，很多学者对它作了研究修改，但是在含根区间内既要保持其收敛速度，又要在所考虑f'(xk)≠0这一苛刻条件，两者不可以兼得，所以可从另外的角度来考虑该问题。

在文献[2]中，给出了一种适合于迭代求复根的抛物牛顿法，这种新型迭代求解非线性方程的复数根方法，它在牛顿法失效时可替代使用。同时，对于实系数多项式，它可迭代出全部根，包括其实根和复根，其收敛程度也比牛顿法快。但是每迭代一次都需要求函数的二阶导数f″(xk)，如果函数在xk处的导数不存在，则此方法失效。本文针对抛物牛顿法存在的问题，将其进行了改进推广，用传统的割线代替切线思想，对抛物牛顿法进行修正，得到一种新方法——抛物牛顿割线法。它能有效克服上述这些方法的缺点，而且收敛速度比经典的牛顿迭代法快。

1 抛物牛顿割线法的构造

设f(x)=0是非线性方程，x=xk为f(x)=0的一个近似解，若f(x)在xk的某个领域内三阶可导，现将f(x)在点xk处用泰勒公式二阶展开，即

则当x∈U(xk)，f(x)≈h(x)，令h(x)=0

解方程得

以此作为f(x)=0的一个近似解，并构造抛物牛顿割线法迭代格式[2]如下:

抛物牛顿割线法构造思想为:假设f(x)在xk的某个领域内三阶可导，将f(x)在xk处用Taylor公式二阶展开，按照传统的割线法类似的思路，即用差商代替导数，提出一种新的迭代方法，迭代格式为

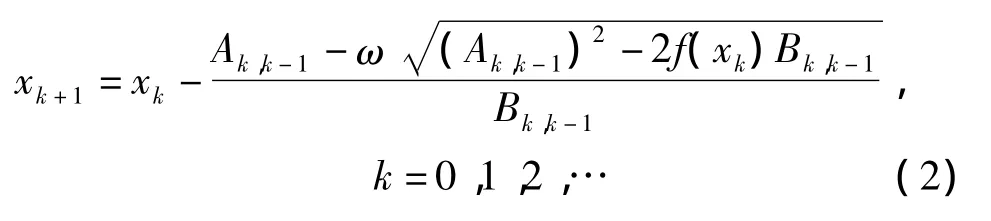
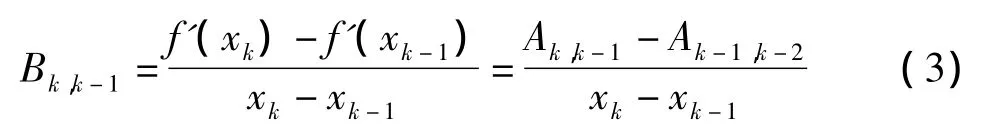
式(3)中的Ak，k-1，Bk，k-1采用双点割线法进行计算。

若采用单点割线法进行计算，则计算公式为:

ω的取值应使解xk+1比xk更接近解x*，为方便计算可取ω=±1.

定理1 设f(x)=0是非线性方程，s为f(x)=0的一个根，若f(x)在s的某个领域内三阶可导且f″(x)≠0，则存在 ε ＞ 0，当x-1，x0∈Iε时，则由式(2)产生的序列收敛于方程的根。

抛物牛顿割线法符号ω可正可负，它意味着近似的抛物线或近似方程在复数域上的两个解。已知牛顿切线法至少是二阶收敛的，抛物牛顿法是三阶收敛[2]的，所以抛物牛顿割线法的收敛速度应该在二者之间，而且迭代中不需要导数的计算，可计算性和适应性增强，后面的数值实验也验证了这个事实。

2 抛物牛顿割线法的几何解释

从几何上看，如果在迭代点所作的抛物线g(x)=与x轴相交，则抛物牛顿割线法是将曲线f(x)上过点p(xk，f(xk))的抛物线与x轴的交点来代替f(x)与x的交点，抛物线g(x)与f(x)在点p(xk，f(xk))相交且具有相同的凹凸性，从而将抛物线g(x)=0的解可作为f(x)=0的一个新的近似解。

3 数值实验

解 易知在复数域内，5次的实多项式应恰有5个根。该曲线有3个实根和一对共轭复根，若用牛顿切线法，仅能求出其3个实根。采用抛物牛顿割线法计算如下:采用公式0，1，2，…进行迭代，式中Ai，j，Bi，j由式(4)进行计算，计算结果如表1和表2所示。

表1 抛物牛顿割线法取(ω=1，x0=-10)时与牛顿切线法和抛物牛顿法迭代比较

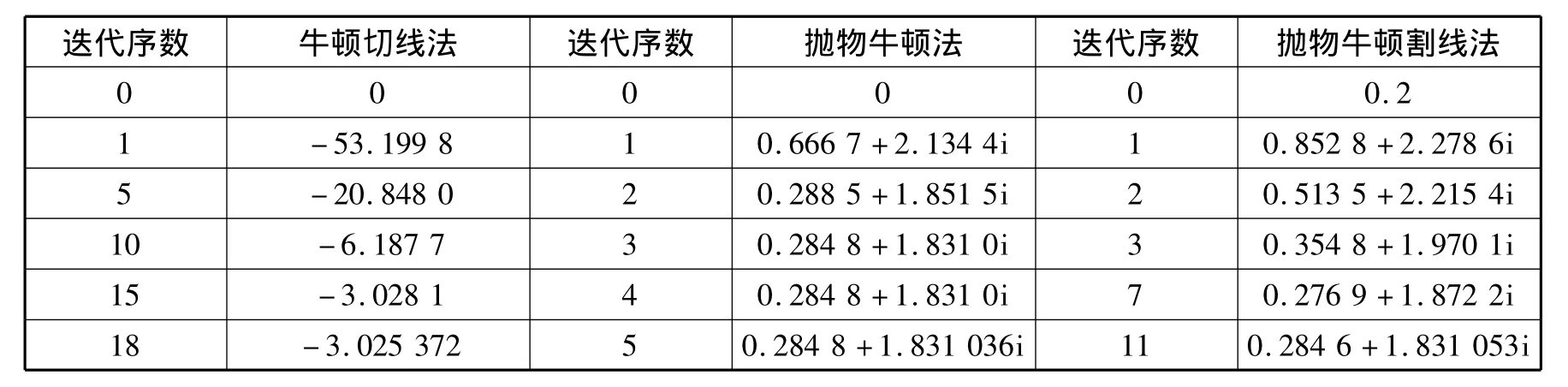
表2 抛物牛顿割线法取(ω=1，x0=0)时与牛顿切线法和抛物牛顿法迭代比较

同理，取 ω =1，x0=8，x-1=10，经过 5 次迭代可获得方程的近似根9.375 676，牛顿迭代法需要5次，抛物牛顿法需要3次迭代。取ω=-1，x0=6，x-1=8，经过6次迭代可获得方程的近似根3.080 095，牛顿迭代法需要7次，抛物牛顿法需要4次迭代。由于实系数多项式的复根成对出现，所以方程的另一个复根为0.284 8-1.831 036i.

算例2 求方程x-lnx=2在(2，∞)的根，计算中要求精确到10-8.

解 采用式(2)-(3)进行迭代计算，计算结果列于表3，结果表明抛物牛顿割线法具有相当的收敛速度，且不受导数条件的限制。

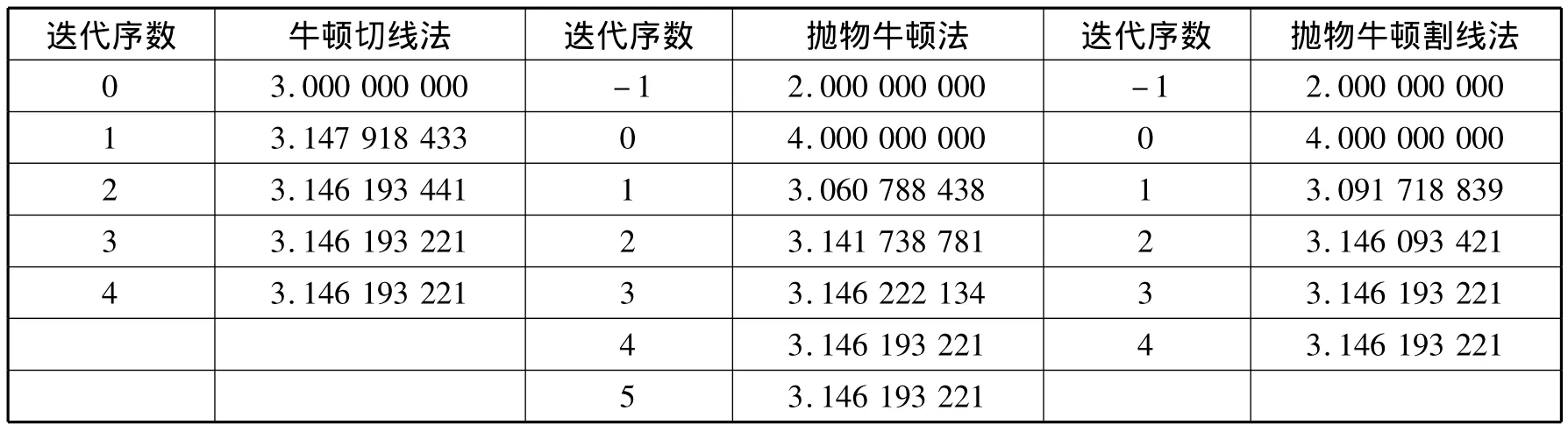
表3 抛物牛顿割线法取ω=1时与牛顿切线法和牛顿割线法迭代比较

4 结论与展望

本文提出了一种新型求解非线性方程的迭代方法——抛物牛顿割线法，它不需要函数在节点处导数信息，计算速度比牛顿迭代法要快，实质上相当于对牛顿割线法的一种加速，可以迭代求解复数域内实系数多项的全部解。对于方程组有类似的结论，但方法将复杂的多，同理对于实系数多项式方程组，也能迭代出复数域内全部的实根和复根。但是和抛物牛顿法相比，抛物牛顿割线法是多步方法，收敛速度没有抛物牛顿法快，其优点是不需要求函数在迭代节点处导数值，计算工作量要小，在牛顿法和抛物牛顿法失效的情况下，此方法可以继续迭代计算。

[1]吴新元.对牛顿迭代法的一个重要修改[J].应用数学和力学，1999，20(8):863-866.

[2]王礼广，熊岳山，蔡放.一种适合于迭代求复数根的抛物牛顿法[J].湖南师范大学学报:自然科学版，2007，30(4):11-14.

[3]颜庆津.数值分析[M].北京:北京航空航天大学出版社，2000.

[4]周智恒，范毅，廖芹.一元实系数多项式方程根的求解问题[J].华南理工大学学报:自然科学版，2002，30(5):8-11.

[5]WILKISION J H.代数特征值问题[M].石钟慈，译.北京:科学出版社，1987.