基于小波变换的臂丛神经损伤后疼痛患者脊髓电信号分析

李 东 胡永生 柳 渊 白 玫

1 引言

臂丛神经损伤（brachial plexus）是周围神经损伤的一个常见类型。常因牵拉、对撞、挤压和切割造成臂丛损害。臂丛神经损伤后常伴随疼痛的发生。脊髓背根入髓区（dorsal root entry zone，DREZ）切开术对脊髓损伤后慢性疼痛疗效满意，可明显提高患者的生活质量。选择并掌握切开的范围、深度和角度是提高疗效、避免并发症的关键所在。本文通过对外伤性臂丛神经损害患者的针电极资料进行分析，以探讨其对辅助判断臂丛神经损伤修复的部位、程度、范围及预后等方面的价值。在手术中进行脊髓电信号的检测，并实时分析其频率特性，就可以应用于术中监测DREZ是否成功进行。

信号分析理论中小波变换具有多分辨力特性，无论是在时间域还是频率域都能很好的细化被分析信号，被称为是数学上的“显微镜”。作者应用小波理论，对8例臂丛神经损伤后疼痛患者应用脊髓后根入髓区切开术的术前术后、健侧患侧脊髓电数据进行分析处理。旨在讨论其对手术指导的意义。

2 方法

经典的傅里叶变换表达出信号的频域特征，适用于线性条件下处理平稳信号，然而如同脑电信号一样脊髓电信号也是随机非平稳信号。这就需要可以同时显示信号时域和频域特性的时频分析方法来处理。小波变换以其多分辨率的优势成为时频分析理论中较为重要的方法。

小波变换最早是由法国数学家Meyer等构成较系统的理论框架，而法国学者Daubechies和Mallat在将小波理论引入工程应用方面做了很多的工作[1-2]。近些年对小波变换的研究已经使小波技术成为完善成熟的非平稳信号分析方法，并且已经应用到了除了医学信号处理之外的其他领域。在语音识别、医学图像处理等方面小波变换也有较为重要的应用。小波变换具有以下几个特点：①多分辨率(多尺度)；②品质因素，即相对带宽(中心频率与带宽之比)恒定；③选择适当的基本小波，可使小波在时、频两域都具有表征信号局部特征的能力[3]。

2.1 小波分析基本思想

传统的傅里叶变换就是将一个信号表示成一系列正弦和余弦函数之和。而小波变换则是用母小波通过移位和缩放后得到的一系列小波表示一个信号的变换过程。这里的小波是指在有限时间范围内变化且其平均值为零的数学函数。具有有限的持续时间和突变的频率和振幅。连续小波变换的定义为：

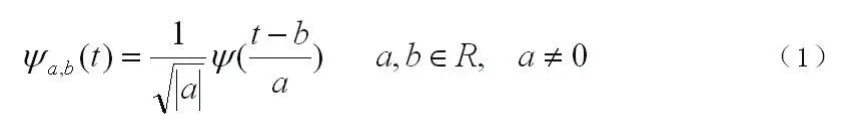
当小波变换的平移因子和尺度因子为离散情况时称为离散小波变换，特别当尺度为二时，称为离散二进小波变换[5]。用离散二进小波变换处理信号时带宽以二的指数幂减小，由于工程实际中采集到的信号多为离散形式的数字信号，因此在数字信号处理技术中常采用离散二进小波变换的方法，离散二进小波分解及合成的基本原理如下：

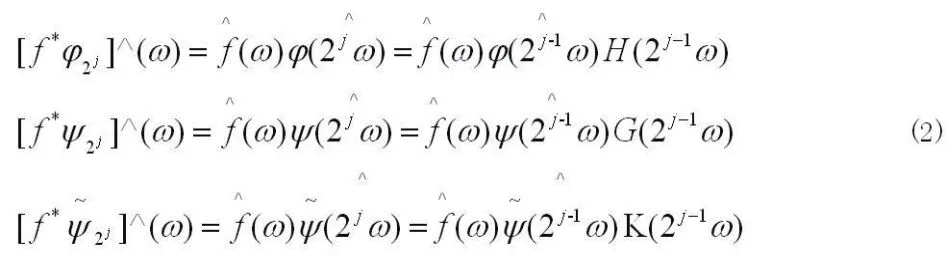
2.2 Morlet小波的选择

在小波分解的过程中，小波函数不断地进行着平移、伸缩，这就使原始信号在各个层面上分解，那么小波函数也都成为其成分的基本单元。在频率从低频到高频变换的过程中，小波函数窗口会逐渐缩小，也就是说分析结果在低频段拥有高频率分辨率和低时间分辨率，而在高频段有低频率分辨率和高时间分辨率。这样看来选择适合原始信号的小波函数对实验的结果有着关键的作用。

选取小波函数时一般基于以下几个原则：自相似，原则选取的小波与被分析波形有一定的相似性；正则性，小波函数的正则性反映了光滑程度，正则性越高，小波基越光滑，它影响着小波系数重构的稳定性；消失矩，消失矩越高，光滑函数在小波展开式中的零元越多；紧支性，支集越短的小波，局部化能力越强，越有利于确定信号的突变点，而且支集越短的小波，产生的大幅值的小波系数就越少；另外，短支集能提高计算速度[6]。然而，在实际操作过程中，对于特定的信号有较好分析结果的小波函数还是最优的选择。

典型的小波函数主要有哈尔基函数(Haar Basis Function)、Morlet小波、Marr小波 DOG（Difference of Gaussian）小波和Shannon小波。其表达式分别为：

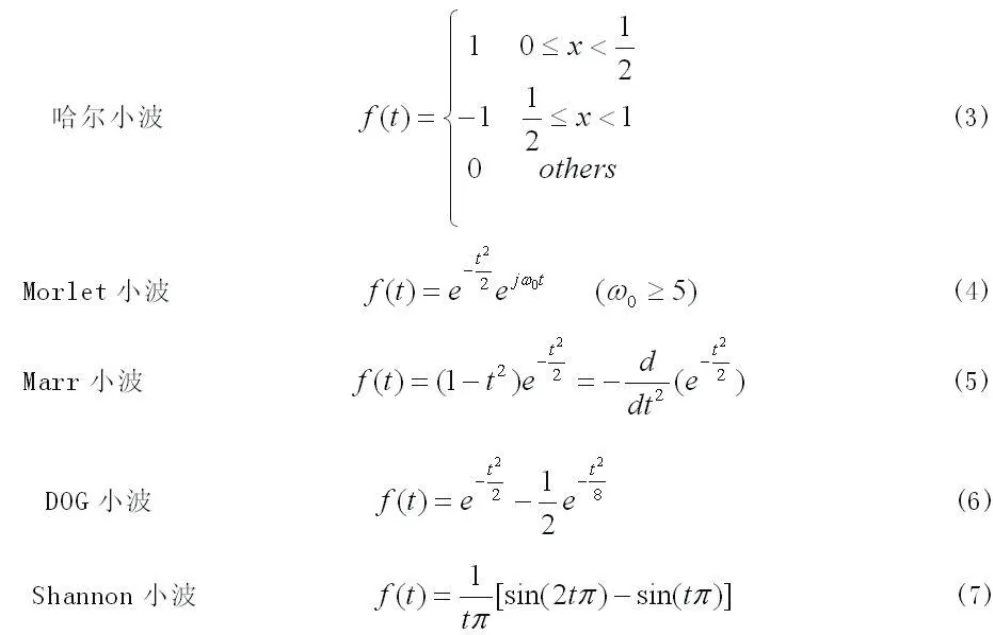
一维Morlet小波傅里叶变换为Gauss函数[7]，又Morlet小波是非正交小波基,离散后可以实现任意高的频域或者时域分辨率[8]。采用Morlet小波和db10小波分别进行了信号分析，经过对比选用Morlet小波。

3 实验过程

3.1 实验数据

文章所举实验数据采自首都医科大学宣武医院功能神经外科收治的臂丛神经损伤后疼痛患者，行患侧C4—T1 DREZ切开术治疗，术中脊髓电图记录监测，可供分析的脊髓电图15例，年龄为38～68岁，中位年龄52岁。

信号采集系统为该院所属意大利Medcare Da Vinci数字信号采集系统。数据由8个电极记录，采样频率128 Hz。高通0.5～0.8 Hz，低通80～100 Hz，增益30～80 μV。患者颈项部后正中切口，全身麻醉。麻醉前患者左肩和左锁骨上窝固定2个表面盘状电极，分别作为参考地线和心电电极。暴露脊髓后表面，将参考盘状电极固定于术区椎旁肌肉表面。记录电极是一6触点或8触点条片电极，置于暴露的脊髓表面。DREZ切开前在健侧及患侧脊髓DREZ分别记录，DREZ切开后，再次记录患侧DREZ的后角自发场电位。每次记录时间5 min。

鉴于手术过程中，脊髓电数据受到的干扰较大，筛选出其中较为完整的8例为本组研究对象。每例三组数据，分别为患侧术前数据、健侧术前数据和患侧术后数据。每组含六导双极导联，并截取其中较为稳定、干扰较少的5 s作为分析数据。

3.2 实验结果

基于小波变换的理论，使用MATLAB7.0编写算法程序。选择其中一例，将各个导联的患侧术前、健侧术前和患侧术后的小波分析图进行对比。结果见图1：

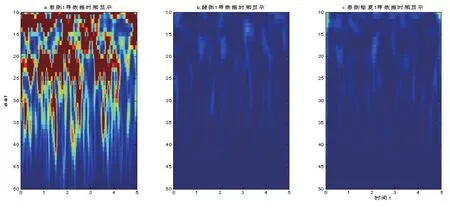
图1 第一导联数据的小波变换时频能量图

从图中可以明显看出，除了10 Hz以下的生理电信号干扰以外，患侧术前电极记录数据在20～30 Hz频段呈高能量，但是在健侧数据和手术修复后的患侧数据并无此高能量频段。

这4个导联的分析结果与第一导联相似，也都出现了患侧电极记录数据在20～30 Hz频段呈高能量，与此相应的，在健侧数据和手术修复后的患侧数据并无此高能量的特征。

4 结论

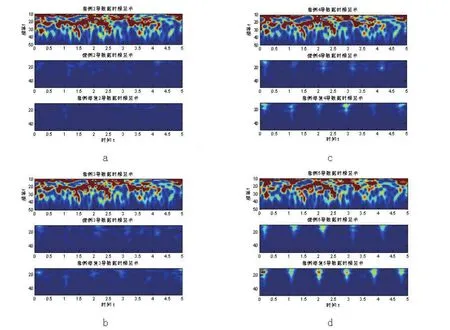
图2 a.第二导联数据的小波变换时频能量图b.第三导联数据的小波变换时频能量图c.第四导联数据的小波变换时频能量图d.第五导联数据的小波变换时频能量图

通过以上对比可以明显看出，在频率域上患侧的电极记录数据在20～30 Hz频段的能量值明显高出健侧术前和患侧术后数据。在其余七例患者的电极记录数据分析中也可以明显看出此现象。也就是说疼痛患侧的电信号较多集中在20～30 Hz频段，而健侧则没有这一特征。在手术进行中，可以利用这一特性指导手术的进行。

[1]Mallat SG.A theory for multiresolution signal decomposition[J]：the wavelet representation[J].IEEE Trans PAMI,1989,11(7):674-693.

[2]Daubechies I.Where do wavelets come from?—A personal point of view[J].Proc IEEE,1996,84(4):510-513.

[3]胡益斌.磁导航技术在心脏介入手术中的应用[J].医疗设备信息,2006,21(7):49.

[4]陈颖萍,林家瑞.基于小波变换和独立分量分析相结合的癫痫脑电分析[J].生物医学工程研究,2006,25(1):9-13.

[5]陆英北,张增芳,蔡坤宝.基于小波变换的心电信号基线矫正方法[J].北京生物医学工程,2000,19(4):235-239.

[6]王佳文,凡友华.心电信号去噪中的小波方法[J].数理医药学杂志,2009,22(1):85-89.

[7]卢新城,龚沈光,周骏,等.基于Morlet小波的高分辨率信号频谱估计[J].武汉理工大学学报,2002,26(5):622-635.

[8]岳林，张令弥.基于Morlet小波的信号滤波方法及在频率响应测试中的应用[J].数据采集与处理,2002,17(4):459-462.