基于小波变换的变压器差动保护算法

高志勇，成建军，张昕

(二滩水电开发有限公司，四川 成都 610041)

1 引言

据统计［1，2］，1999 年我国运行中的 220kV 变压器有2526台，330kV变压器有102台，500kV变压器223台。到2002年底，我国运行中的220kV变压器达到3229台，330kV变压器有122台，500kV变压器有295台。然而多年来电力系统变压器保护的正确动作率却大大低于发电机和线路保护的正确动作率。以2007年为例，全国继电保护的运行情况是:200kV及以上母线保护装置正确动作率达96.72%;100MW及以上发电机保护装置正确动作率为99.74%;220kV及以上变压器保护装置正确动作率仅为96.49%。

差动保护一直用于变压器主保护，但如何正确鉴别励磁涌流和内部故障电流一直是变压器差动保护的核心问题。采用二次谐波制动原理的变压器保护较为常见，但也面临着一些问题［3－5］:对暂态信号的励磁涌流进行傅里叶级数的谐波分析，傅里叶级数法的周期延拓将导致错误的结果;同时二次谐波制动系数一直都没有统一的标准;变压器在满足一定条件时，三相励磁涌流的二次谐波含量可能均小于15%［6］，因此可能使保护出现误动。

本文通过在PSCAD/EMTDC中建立电力变压器典型励磁涌流和内部故障模型，通过小波变换研究电流波形数据从而获取确鉴别励磁涌流和内部故障的判据和算法。

2 小波变换简介

设函数ψ(t)∈L2(R)，满足如下条件:

则称ψ(t)为基小波或母小波。引入尺度因子a和平移因子b，a和b满足:a，b∈R且a≠0。将基小波进行伸缩和平移，得到如下的函数族:

称 ψa，b(t)为小波分析。

对于函数f(t)∈L2(R)，若满足如下“容许性”条件:

则连续小波定义为:

显然，小波函数ψ(t)的伸缩和平移表现了它对信号不同频率和不同时间位置的限制，ψa，b(t)可作为时窗函数，ψ^a，b(ω)可作为频窗函数。

连续小波变换CWTa，b存在逆变换，逆变换公式为:

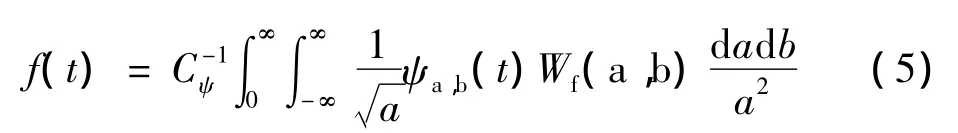
数学上称无限次可导的函数是光滑的或是没有奇异性，若函数在某处有间断或某阶导数不连续，则称函数在该处具有奇异性。该点称为信号的奇异点，并用Lipsehitz指数描述其奇异性，简称Lip指数，记作α［7］。

若函数(信号)f(t)在某个局部点t0处间断或导数间断，则称该函数在t0处有奇异性。若存在一常数c使下式成立:

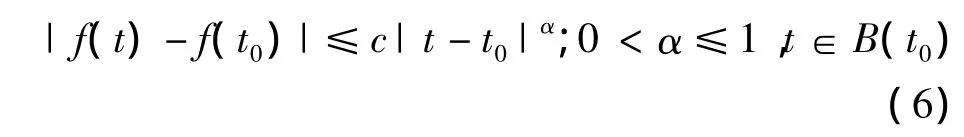
则称f(t)∈(B(t0))。其中C是与t和α无关的有界常数;B(t0)是t0为中心的某个领域。

显然当α=1时，函数(信号)是连续可导的;0＜α＜1时函数的光滑性降低，甚至不连续;α越小，f(t)在t0处的奇异性程度越高。因此α给出了信号f(t)在t0点的可微性即光滑度的精确信息。

由上述的分析可知，函数(信号)的奇异性可用Lip指数来刻划，其数值可通过小波变换的模极大值在不同尺度下的数值计算出来。α＞0时，小波系数的模极大值随尺度因子增大而增大;当α＜0时小波系数的模极大值随尺度因子的增大而减小;当α=0时，小波系数的模极大值与尺度因子无关。如果t0是信号f(t)突变点，那么在各尺度t0点附近都会产生一个局部极大值点，并且随着尺度的减小，这些模极大值点收敛于。因此可利用小波变换模极大值检测出信号f(t)上的所有突变点，也可测得突变点奇异性的大小。

Db小波是为小波分析的推广应用做出巨大贡献的著名学者InridDaubechies构造的小波函数，通常简写为DbN，N是小波的阶数，Db小波是正交小波。Db小波ψ(t)和尺度函数φ(t)的支撑长度为2N－1，ψ(t)的消失矩为N。除N=1外，DbN不具有对称性(即非线性相位)。DbN没有明确的表达式。对正交小波来说，小波消失矩与其支撑集长度有十分密切的关系，Daubechies已证明，若小波有k阶消失矩，则其支撑集长度至少为2k－1，对于给定的消失矩，Db小波有最小的支集，从这个方面来说，Daubechies小波是最优的。由于支集长度和消失矩之间的关系，选择正交小波时，必须在支集长度和消失矩阶数之间折衷。如果信号有很少的孤立奇异点，在奇异点之间很光滑，应选择具有高阶消失矩的小波以使大量的小波系数幅值很小。而当奇异点靠得很近时，最好选择支集长度较小的小波，以便于区分这些奇异点，同时也可以减少大幅值的小波系数，并且增加支撑集长度导致计算量上升，落实到具体应用时则应该看具体使用情况来选择。本文中则采用Db3小波函数作为分析工具。

3 数据分析

内部故障主要模拟单相接地、两相短路、两相短路接地故障。设定在0.2s时发生故障，对电流信号每工频周期采样200点，即采样频率为10kHz，以空载合闸和故障时刻为起点，对一、二次侧采样电流一工频周期时间内的信号数据进行小波分析。励磁涌流仿真具体参数见表1，数据采集范围从0～0.6s。

表1 三相变压器励磁涌流仿真参数

研究表明［8］，对于三相变压器来说，无论在任何瞬间空载合闸，至少有两相要出现程度不同的励磁涌流，而另一侧三相励磁电流则全部接近0(数量级为E－9)。由于变压器励磁涌流仅流经变压器电源侧，因此在差动回路中不能被平衡。

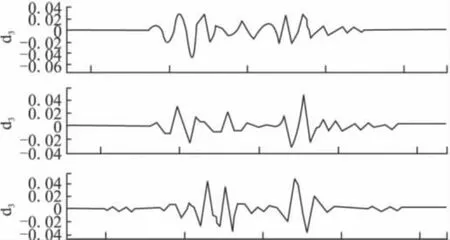
图1 情况1，α=0°时ABC三相一次侧电流小波变换

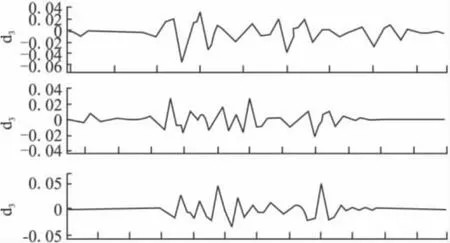
图2 情况1，α=45°时ABC三相一次侧电流小波变换

限于篇幅，仅列举出情况1时A相合闸角为0°和45°各相一次侧电流经小波变换后的波形。研究后可以看出:无论电源侧励磁涌流波形偏向于时间轴一侧还是以时间轴为对称，经过小波变换后，对应于间断角处(相当于突变奇异点)总是存在模极大值，并且发生励磁涌流的第一个工频周期时间范围内其模极大值绝大多数情况下出现在1/4工频周期后;二次侧小波变换后的模极大值为零(数量级为E－9)。

当设定变压器A相发生接地故障时，图3为发生故障后A、B、C三相各自小波变换后的一、二次侧电流波形。

图3 A相接地短路时，ABC三相一、二次侧电流小波变换

由以上波形可以看出:A相在故障发生后的一工频周期时间范围内的模极大值不仅对应或者接近于故障发生时刻，并且一、二次侧的模极大值符号相反且绝对值分别为0.0149和0.00804;B相一、二次侧在故障发生后的一工频周期时间范围内的模极大值的绝对值分别为0.00589和0.00046;C相一、二次侧在故障发生后的一工频周期时间范围内的模极大值的绝对值分别为0.006025和0.007635。

当设定变压器AB相间发生短路故障时，图4为发生故障后A、B、C三相各自小波变换后的一、二次侧电流波形。

由以上波形可以看出:故障相在故障发生后的一工频周期时间范围内的模极大值不仅对应于故障发生时刻，并且A、B相一、二次侧的模极大值符号相反且绝对值分别为0.0707、0.0519和0.0708、0.0261;C相一次侧在故障发生后的一工频周期时间范围内的模极大值的绝对值分别为0.000685和0.0257。

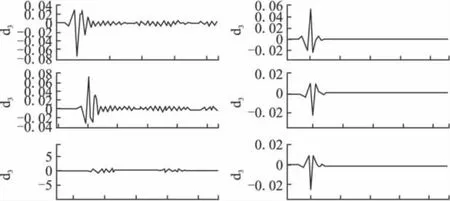
图4 AB相间短路时，ABC三相一、二次侧电流小波变换

当设定变压器AB相间发生短路接地故障时，图5为发生故障后A、B、C三相各自小波变换后的一、二次侧电流波形。

图5 AB相间短路接地时，ABC三相一、二次侧电流小波变换

由以上波形可以看出:故障相在故障发生后的一工频周期时间范围内的模极大值不仅对应于故障发生时刻，并且AB相一、二次侧的模极大值符号相反且绝对值分别为0.0412、0.0519和0.1、0.0595;C相二次侧在故障发生后的一工频周期时间范围内的模极大值的绝对值分别为0.057和0.00765。

上述仿真研究是基于直接对一、二次侧电流进行信号采样分析而得到的结果，而实际工程运用中由于考虑到绝缘和安全的因素，无法将线路上的大电流直接接入保护回路进行数据分析，因此在假定电流互感器是线性传变的同时，通过使用变比适当的电流互感器将变压器两侧的电流信号转换后接入差动保护回路进行信号处理。而电流互感器由于也大多为铁磁材料制作同样存在着饱和问题并一直受到继电保护工作者的长期关注。CT饱和主要分为暂态饱和和稳态饱和。对于电压等级较低的电网，一般只要有所注意，保护装置适应电流互感器的稳态饱和并无太大困难。但在更高一级电压的电网中，要满足快速保护对电流互感器过渡过程饱和时的要求就要复杂得多，原因是故障电流初始值中含有直流分量。

实际上，无论是在励磁涌流，还是在故障过程中，都有可能出现电流互感器的饱和。但是由故障开始到电流互感器开始饱和总是有一个过程，电流互感器的饱和不是从故障开始就立即出现，而只能在一定时间之后才发生，这一时间段至少有四分之一个周期［9］。而本文仿真得到的电流数据，虽然时间范围是一个工频周期，但所需要的部分往往均在1/4周期内，因此本文所设计的模型可以认为基本不受CT饱和的影响。

关于环境中的电磁噪声对小波变换模极大值所产生的影响，理论上可以通过对噪声与信号突变点的小波变换模极大值在不同尺度下的传播特性不同加以解决［10］。噪声的小波变换模极大值幅度和平均稠密度通常随尺度的增大而减小，而信号的小波变换模极大值随尺度的增加不衰减。因此可以通过设置一定的尺度来有效去除噪声的干扰。

4 保护算法设计

根据上述仿真研究结果表明:当发生励磁涌流时，虽然变压器电源侧涌流的幅值能达到额定电流的数倍，但是在另一侧电流却几乎为零(数量级仅为E－9)，对应的模极大值也可以认为是为零的;对于发生单相接地、两相短路、两相短路接地等典型故障情况，故障发生相两侧对应的模极大值点的幅值其正负性是相反的，若采用适当的门槛值，将模极大值过小的点归结等同于是为零，则可以认为非故障相两侧的模极大值点总是有存在为零的情况。

对应于本文的具体仿真数据，可设定门槛值K为0.008，低于该数值的模极大值均设定为零。可以看出，此门槛数值可以较好的区分出励磁涌流和故障电流，并且当某相一旦发生故障时，其一、二次侧电流信号模极大值点处电流幅值符号相反，即乘积为负;而正常相的乘积则为零。因此不但可以依据其乘积的符号对励磁涌流和故障电流做出判断并且可以进一步判断出故障所在相，并且可以保证判断的准确。

在分析励磁涌流时一次侧波形时，我们可以看到，一个工频周期内的电流模极大值出现的位置往往在1/4周期后，但是有些情况下也有少量模极大值出现在1/4周期内或者极接近1/4周期处;而上述几种典型故障情况下各相电流的模极大值均出现在故障发生时刻或接近于发生时刻处。考虑到现场电磁情况的复杂以及差动保护整定时往往为了避开各种不平衡电流等不利因素的干扰，保护回路启动时刻与励磁涌流发生时刻并不一致，因此单凭分析一周期内模极大值出现的时间位置也不能足以在任何情况下都让保护回路做出准确判断并动作。但是可以考虑将其作为进一步判断是否为故障电流还是励磁涌流的依据，以尽可能的减少误判导致拒动的可能性。

综上所述，所设计的判据如下:

设变压器差动保护回路分别在三相各自独立判断，I1(t)、I2(t)分别为采样区间内某相一、二次侧电流小波变换模极大值点的幅值，设K为门槛值且K=0.008，若

则在差动回路中的不平衡电流高于整定值时，若数据运算后S＜0，可判断该相发生内部故障，差动保护回路发出信号“1”;若小波变换后某相一次或二次侧电流幅值低于门槛值K则S=0，差动保护回路发出信号“0”，采用逻辑“或”判断，将三相发出的“0”和“1”进行“或”运算，若结果为“1”则差动保护发出跳闸信号，若逻辑判断结果为“0”(如上述匝间短路情况)则将一周期内的电流信号进行进一步分析，若发现至少存在一相的一次侧电流模极大值出现在1/4工频周期时间范围内，则可以认定此种情况为内部故障，差动保护发出跳闸信号。反之差动保护则发出闭锁信号，延迟一定时间后保护回路复位继续进行判断。更进一步，除了能保证发生故障时断路器分断，也可利用各相反馈回的“0”“1”信号判断具体故障发生在哪一相。

考虑到实际工程应用中电磁环境的复杂，该判断方法还需要进一步调整以适应现场环境。若门槛值K选取的不足够合理，比如过高，有可能仅凭S的数值判断某些轻微故障情况，并不能做到足够准确的判断，甚至会导致拒动情况发生，最终引起更严重的事故。这也是为什么在设计保护方案的时候增加了备用方案，虽然两者单独使用均不能做到绝对正确，但是综合运用的情况下则能大大降低误判的可能性;若K值设定偏低，也不会造成保护装置的误动进而影响电力系统的可靠运行，仅仅会在发生故障的情况下除了能正确判断某相存在故障，同时还会错误判断正常相也存在故障。而这样的“误判”所导致的结果除了在故障排除的检修维护过程中增加一定工作量，对电力系统的安全稳定运行并不存在任何实质性的影响，并且该判断依据计算简单，所用数据量较少，能在很短的时间内就对变压器的运行状况做出判断，因此可以说该方法有着一定的可行性和实用性。

［1］王维俭，王祥珩，王赞基.大型发电机变压器内部故障分析与继电保护［M］.北京:中国电力出版社，2006.205－208.

［2］沈晓凡，舒治淮，刘宇等.2007年国家电网公司继电保护装置运行情况［J］.电网技术，2008，32(16):6 －7.

［3］王维俭.变压器保护运行不良的反思［J］.电力自动化设备，2001，21(10):1－3.

［4］“九五”期间全国电网继电保护统计资料汇编［M］.南京:全国电网调度工作会议，2001.

［5］葛宝明，王祥晰，苏鹏声，等.电力变压器的励磁涌流判据及其发展方向［J］.电力系统自动化，2003，27(22):1 －5.

［6］林湘宁，刘沛，刘世明，等.变压器有载合闸的超饱和现象及对变压器差动保护的影响［J］.中国电机工程学报，2002，22(3)，7 －11.

［7］徐丙莲，弈旭明.基于小波变换的信号奇异性分析［J］.数学杂志，2000，24(6):661 －664.

［8］孙国凯，霍利民，柴玉华.电力系统继电保护原理［M］.北京:中国水利水电出版社，2002.123 －124.

［9］KEZUNOVIC，M，KOJOVIC，L.Experimental Evaluation of EMTP －based Current Transformer Models for Protective Relay Transient Study.IEEE Transactions on，1994，9(1):405 －413.

［10］Mallat S.and Hwang W L.Singularity detection and processing with wavelet.IEEE Transaction on Information Theory，1992，38(2):617 －643.