线接触脂润滑热弹性流体动力润滑数值分析

于玫，黄平

(华南理工大学 机械与汽车工程学院，广州 510640)

润滑脂由于其半固半液的膏体状态而具有使用方便，不易流失，能长期保持稳定润滑的特性，其在现代机械的摩擦副中得到了广泛应用。因此，深入研究润滑脂在弹流润滑条件下的特性与机理，对于机械设计和润滑脂应用有着重要的意义。然而，由于润滑脂表现出的强烈非Newton流体特性，造成其弹流理论计算复杂，使得脂润滑的研究远远落后于油润滑弹流理论[1]。

文献[2]基于Ostwald模型建立了脂润滑控制方程，运用多重网格法求得了线接触脂润滑弹性流体动力润滑的等温数值解。然而，接触区温升常常会使得润滑剂的物理和化学性质发生变化，严重时将导致润滑膜破裂和失效，进而在接触表面产生不同程度的粘着磨损，甚至于卡死。虽然这种表面损伤机理目前还不完全清楚，但是，从润滑膜减薄，到随后产生表面粗糙峰接触和擦伤或胶合的整个润滑失效过程中，热效应无疑是一个重要的影响因素。因此，开展热弹流润滑研究对于改善脂润滑线接触零部件的润滑性能和延长其工作寿命具有十分重要的意义[3]。

文中在线接触脂润滑弹流数值分析的基础上[2]，深入分析考虑了热效应后的线接触脂润滑弹性流体动力润滑情况。用基于Ostwald模型建立的修正Reynolds方程和能量方程联合求解，先采用直接迭代法求解Reynolds方程确定出压力分布和润滑膜厚，将其代入能量方程得出润滑膜和接触表面上的温度分布，最后再代回Reynolds方程求解考虑了热效应的压力分布和润滑膜形状。并分析了不同工况下，热效应对脂润滑弹流数值解的影响。

1 基本方程

1.1 脂润滑的一维Reynolds方程

描述润滑脂流变特性的本构方程目前主要采用Ostwald，Bingham及Herschel-Bulkley 3种模型[4]。文献[5]通过大量试验认为国产润滑脂的特性符合Herschel-Bulkley模型，其含有3个参数。而这里认为该模型的特例就是Ostwald模型，两者的特性有较大的共性。文献[6]认为工业上80%的广义Newton体均可用Ostwald模型，其仅需确定2个参数，使用简单，被广泛采用。因此，文中以Ostwald模型为基础建立脂润滑的控制方程。Ostwald模型的本构方程为

(1)

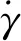
根据(1)式，由文献[7]得基于Ostwald模型的经典脂润滑等效Reynolds方程为

(2)

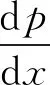
(3)

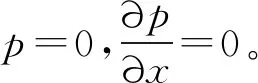
1.2 脂润滑热弹流润滑其他方程

润滑膜几何方程(弹性变形方程)为

(4)

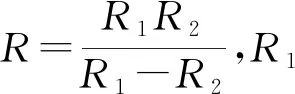
润滑膜能量方程为

(5)

两个接触面上的边界条件为

T0,

(6)

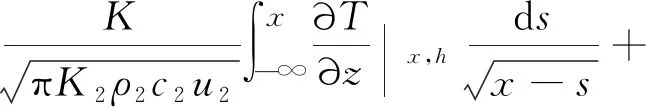
T0,

(7)

运动方程为

(8)

式中：cp，c1，c2分别为润滑剂和上、下表面的比热容；K，K1，K2分别为润滑剂和上、下表面的热传导系数；ρ，ρ1，ρ2分别为润滑剂和上、下表面的密度；T为润滑膜或两表面温度，T0为环境温度；u1和u2分别为上、下表面切向速度，两表面切向速度分别为

(9)

s′为滑滚比。

润滑脂黏度与压力和温度的关系为

φ=φ0exp{(lnφ0+9.67)[(1+5.1×

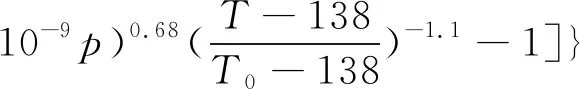
(10)

润滑脂密度与压力和温度的关系为

ρ=ρ0[1-6.5×10-4(T-T0)],

(11)

式中：φ0，ρ0分别为润滑剂的环境黏度和环境密度。

2 数值方法

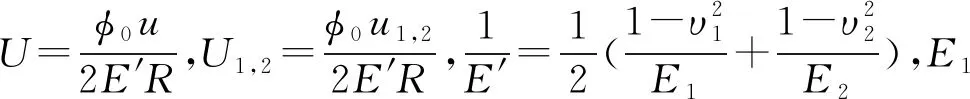
方程的完全数值求解通过压力-温度的循环计算来实现[9-10], 即在Reynolds方程和能量方程之间反复迭代。压力求解采用多重网格方法, 弹性变形的计算采用多重网格积分法，能量方程的数值计算采用步进方法求解[11]。润滑膜温度场计算的特点是：润滑剂在供给温度下进入润滑膜入口，此后润滑剂的温度随着流动而逐渐变化。

3 结果与讨论

所选润滑脂的物性参数为：φ0=0.08 Pa·s，ρ0=890 kg/m3，c=2 kJ/(kg·K)，K=0.14 W/(m·K)；固体的物性参数为：ρ1,2=7 850 kg/m3，c1,2=470 J/(kg·K)，K1,2=46 W/(m·K)(认为两固体材料相同)，其他固定的输入参数包括：T0=303 K，R=0.02 m，E′=221 GPa，s′=0.25。

根据运算结果可以对线接触脂润滑热弹性流体动力润滑进行分析。图1显示出热弹流润滑状态下线接触脂润滑的压力分布和润滑膜形状受载荷、速度及流变指数影响的示意图。相对于等温弹流润滑而言，热弹流润滑的主要特点是考虑了润滑膜温度分布对黏度和密度的影响。由于润滑膜与固体界面之间的热传导，造成沿膜厚方向上温度﹑黏度和密度的变化，虽然润滑膜的热效应对于弹流润滑的压力和膜厚产生了一定的影响，但在基本特性方面，热弹流润滑与等温弹流没有显著的差别。从图1中可以看出，润滑膜压力在入口区处缓慢增加，在出口区处出现二次压力峰；润滑膜厚度在接触中心部分变化平缓，在出口区处出现润滑膜颈缩现象，这与文献[12]得出结果有良好的一致性，证明了计算结果的正确性。

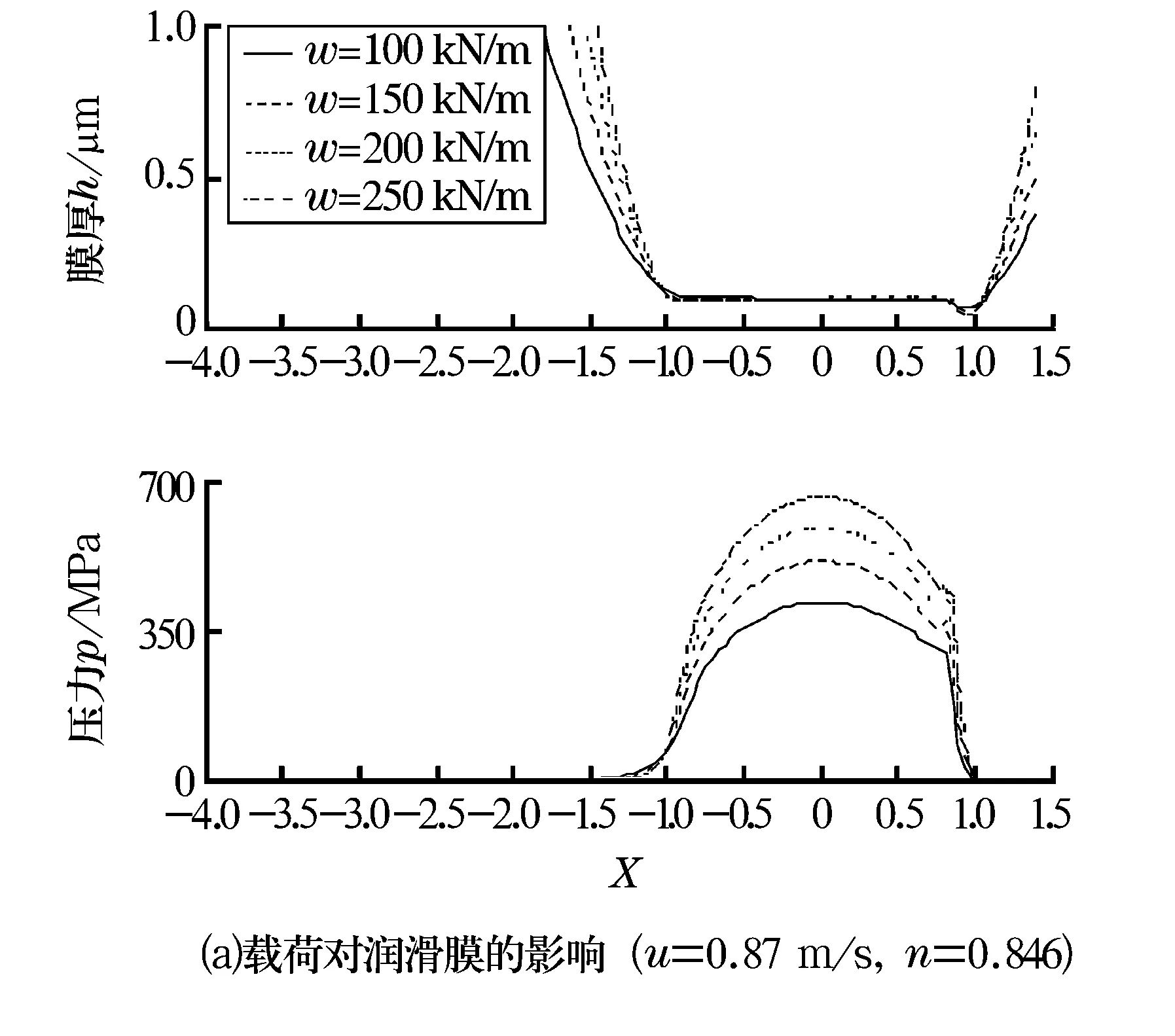
图1 工况参数对润滑膜的影响

图2所示为润滑膜在所受单位载荷w=100 kN/m，平均速度u=0.87 m/s，流变指数n=0.846下沿膜厚方向上的温升图。A，E线所示分别为上﹑下表面的温升情况，其他三条曲线B，C，D表示润滑膜沿膜厚方向上的温升。由图可知，润滑膜和两表面的温度场与压力分布相对应，即在入口区，随着压力增加润滑膜温度也相应升高；而在出口区压力下降处，润滑膜温度急剧减小。在二次压力峰的位置，润滑膜温度呈现一个高峰，但温度峰比压力峰略微滞后。另外，两表面上的温升始终低于润滑膜温升，且运动速度较高的上表面温升低于下表面温升。

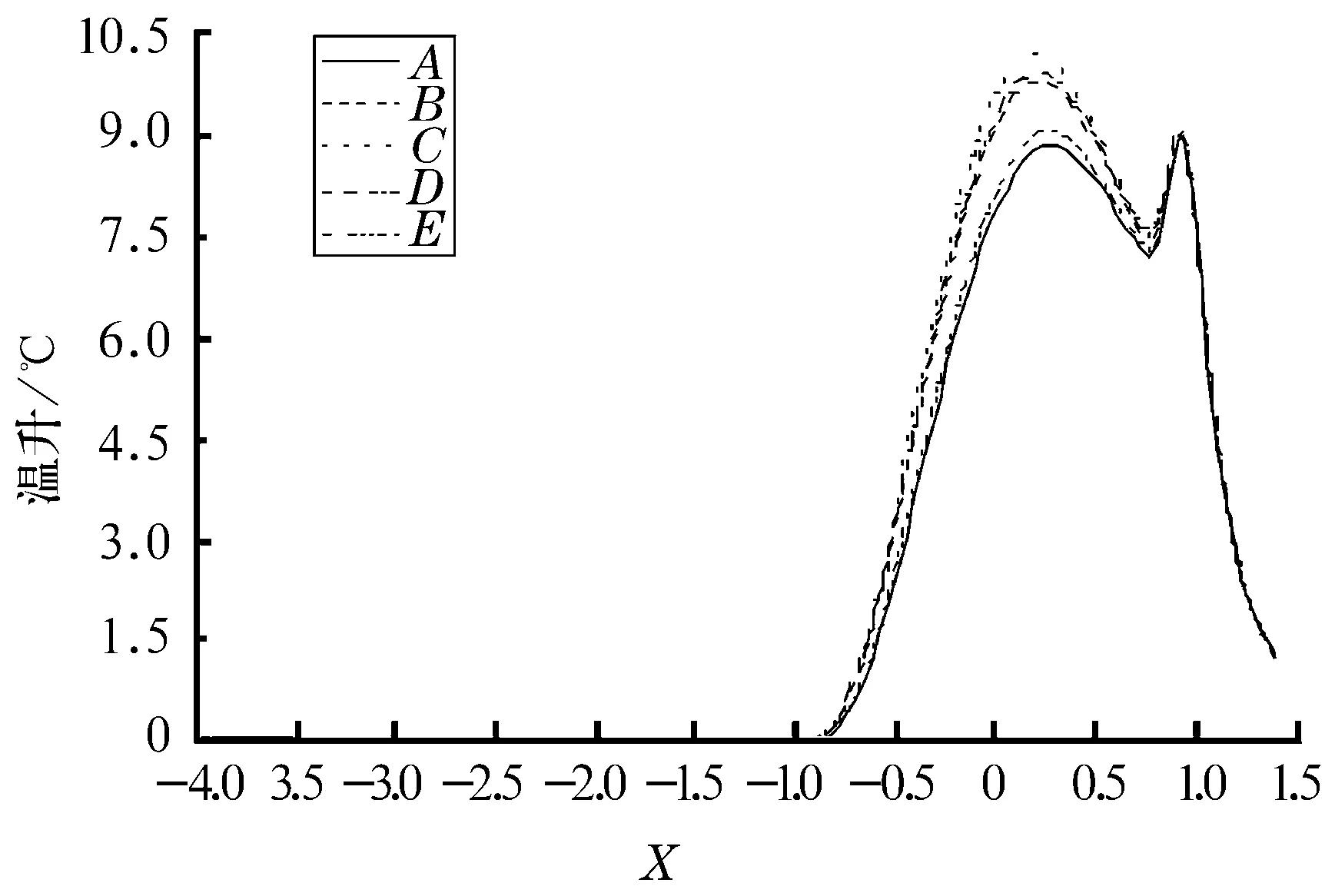
图2 膜厚方向上的温升

图3所示为润滑膜平均温升受载荷、速度和流变参数的影响结果，平均温度为A，B，C，D和E5层的温度平均值。由图可知，载荷、速度和流变参数都会影响到温升，其中，载荷对温升的影响尤其明显，因此载荷是引起弹流润滑温度升高的主要因素之一。润滑膜平均温升随载荷和速度的增加而增加，且在重载和大流变参数条件下，温升曲线都出现了明显的温升峰值。

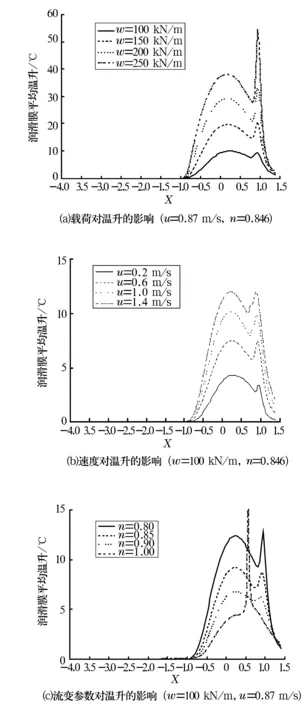
图3 工况参数对平均温升的影响

图4所示为不同速度条件下的等温解与热解的膜厚与压力解对比图。由图可知，随着速度的增大，热解与等温解的差距越来越大。在低速条件下，根据热解求出的压力分布和润滑膜厚度与等温解计算出的结果差别甚小，因此，根据等温弹流润滑公式计算的润滑膜厚度具有足够的正确性。而在速度较大时，热弹流解得到的压力分布和润滑膜厚度与等温解计算结果有明显差别，热弹流解得到的润滑膜厚度始终低于等温解，且速度越大，膜厚差距越大。因此，对于中﹑高速条件下的弹流润滑问题，需考虑热效应的影响。

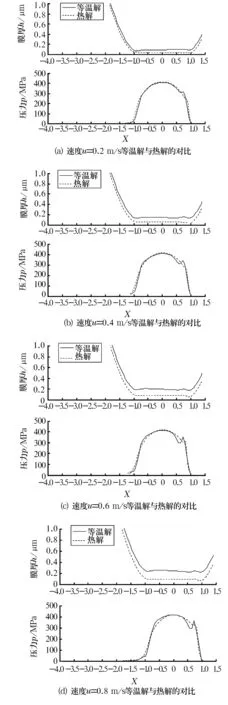
图4 等温解与热解的膜厚与压力解对比(w=100 kN/m,n=0.846)

4 结论

(1)脂润滑热弹流与脂润滑等温弹流的解在润滑特性方面没有本质上的差别，都具有明显的二次压力峰和润滑膜颈缩现象。

(2)脂润滑膜温度场每层的分布曲线与压力分布曲线相对应，运动速度高的表面温升较低，而运动速度低的表面温升较高，但都低于润滑膜内部温升。

(3)载荷、速度和流变参数的改变会显著导致线接触脂润滑热弹性流体动力润滑温度改变，其中重载和大流变系数条件下，温升的曲线会发生明显的温升峰值。

(4)对于脂润滑热弹流问题，低速对膜厚的影响较小，但中﹑高速条件下，由于热效应增强，对膜厚的影响表现显著增强。