基于小波神经网络的风电功率预测

齐放

(华北电力大学，北京 102206)

1 引言

近年来，全球风电发展进入了快车道。截止到2009年，全球风机装机容量已达159231MW，2009年新增装机38312MW。2010年全球的装机容量已超过2000000MW。我国风能资源丰富，据统计，全国风功率密度为100W/m2，风能资源总储量约1.6×105MW，可开发和利用的陆地上风能储量有2.53亿kW。随着人口的增长和环保条件的制约，国家制定了发展新能源的战略，这一举措对促进电力工业调整、推进技术进步等有积极的作用。其中，风力发电是技术最成熟、最具商业化前景和最可能大规模开发的发电技术之一［1－5］。

《中国风电发展报告2010》预测:2020年，中国风电累计装机可以达到2.3亿kW，相当于13个三峡电站;总发电量可以达到4649亿kW时，相当于取代200个火电厂。但与此同时，风电上网难已成为制约风力发电发展的重大瓶颈。开展风电功率预测的研究势在必行。目前国内很多风电场没有装设监测风速、风向、气温等气象参数的实时综合气象监测系统，只是单纯的记录下风机的输出功率，因此针对这种情况，本文利用小波神经网络来进行短期风电功率预测［6，7］。

2 小波理论

小波分析是数学中一个迅速发展的新领域，自从J.Morlet在1974年首次提出小波变换的概念以来，在功率预测、数值分析、故障诊断等领域得到广泛的应用。小波分析是针对傅里叶变换的不足发展而来的，傅里叶变换是信号处理领域中应用最为广泛的一种分析手段，然而它有一个严重的不足，就是变换抛弃了时间信息，变换结果无法判断某个信号的发生时间，即傅里叶变换在时域中没有分辨能力。小波是一种长度有限、平均值为0的波形，它的特点包括两点:一是时域都具有紧支集或近似紧支集;二是直流分量为0。

小波函数是由一个母小波函数经过平移与尺寸伸缩得到，小波分析即把信号分解成一些列小波函数的叠加。

小波变换时指把某一个基本小波函数φ(t)平移τ后，再在不同尺度下分析的信号x(t)做内积。

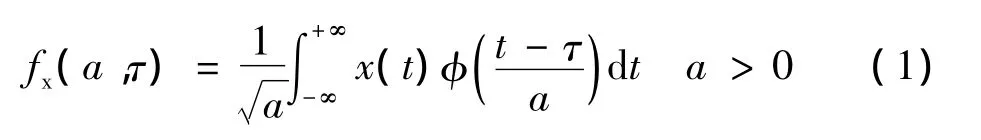
上式可以等效为:

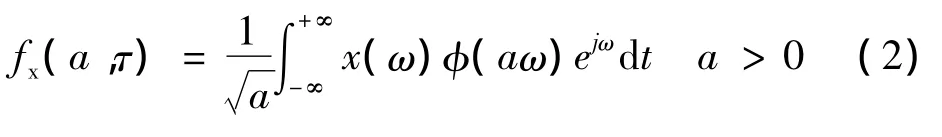
其中，τ是相当于目标平行移动;a相当于使镜头向目标推进或远离。

小波分析能通过小波基函数的变换分析信号的局部特征，并且在二维情况下具有信号方向的选择性能力，因此，该方法作为一种数学理论和分析方法，引起了广泛关注。

3 小波神经网络建模

小波神经网络是一种以BP神经网络拓扑结构为基础，把小波基函数作为隐含层结点的传递函数，信号前向传播的同时误差反向传播的神经网络［8，9］。小波神经网络的拓扑结构如图1所示。

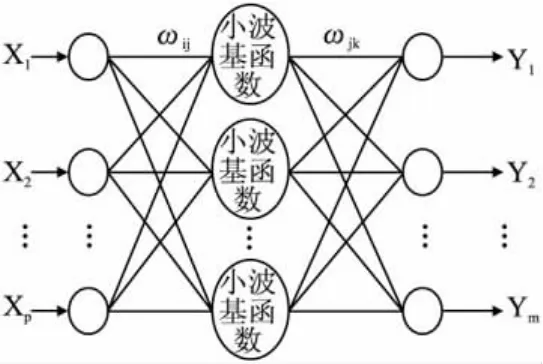
图1 小波神经网络拓扑结构

图1 中，X1，X2，…，Xk是小波神经网络的输入参数;Y1，Y2，…，Ym是小波神经网络的预测输出;ωij和ωjk是小波神经网络权值。

在输入信号序列为xi(i=1，2，…，k)时，隐含层输出计算公式如式(3)所示:

式中，h(j)为隐含层第j个结点的输出值;ωij为输入层和隐含层的连接权值;bj为小波基函数的平移因子;aj为小波基函数hj的伸缩因子;hj为小波基函数。

小波基函数采用Morlet母小波基函数，数学表达式为:

小波网络输出层计算公式为:

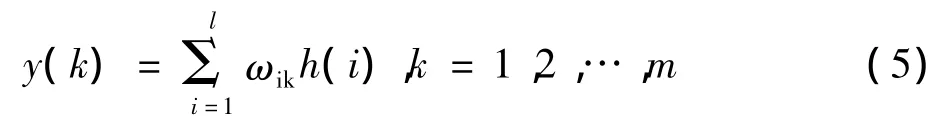
式中，ωik为隐含层到输出层权值;h(i)为第i个隐含层节点的输出;l为隐含层节点数;m为输出层节点数。

小波神经网络权值参数修正算法类似于BP神经网络权值修正算法，采用梯度修正法修正网络的权值和小波基函数参数，使小波神经网络预测输出不断逼近期望输出。小波神经网络算法步骤如下:

步骤1:网络初始化。随机初始化小波函数伸缩因子ak、平移因子bk以及网络的连接权重ωij和ωjk，设置网络学习速率η。

步骤2:样本分类。把风电功率样本分为训练样本和测试样本，训练样本用于训练网络，测试样本用于测试网络预测精度。

步骤3:预测输出。把训练样本输入网络，计算网络预测输出并计算网络输出和期望输出的误差e。

步骤4:权值修正。根据误差e修正网络权值和小波函数参数，使网络预测值逼近期望值。

步骤5:判断算法是否结束，如果没有结束，返回步骤3。

4 算例分析

风电功率某个时刻的输出与前几个时段的功率有关。并且风电功率具有24小时内准周期的特性。程序采用某风电场350个风电功率数据进行仿真验证。为方便处理，对输入输出数据进行了归一化处理，本文采用了式(6)进行处理:

处理后，使得输入输出数据都在(0，1)的范围内，满足函数的具体要求。归一化处理后，利用小波神经网络进行功率预测，具体过程如下:

首先，构建小波神经网络，神经网络的各个参数由仿真对比逐步确定，根据风电功率的特性设计小波神经网络分为输入层、隐含层和输出层三层。其中，输入层输入为当前时间点的前n个时间点的风电功率;隐含层节点由小波基函数构成;输出层输出为当前时间点的风电功率输出。

其次，小波神经网络训练。利用前300个风电功率进行小波神经网络训练，利用训练好的神经网络。网络结构采用5－8－1结构，表示预测时间节点前5个风电功率值，隐含层有8个节点，输出层有1个节点，为网络预测的风电功率值。网络权值和小波基函数在参数初始化时对比获取，用训练数据训练小波神经网络，网络反复训练100次。

最后，利用上述所训练出的小波神经网络对进行风电功率预测。所得的预测值与实际值的对比如图2所示。误差分布图如图3所示。

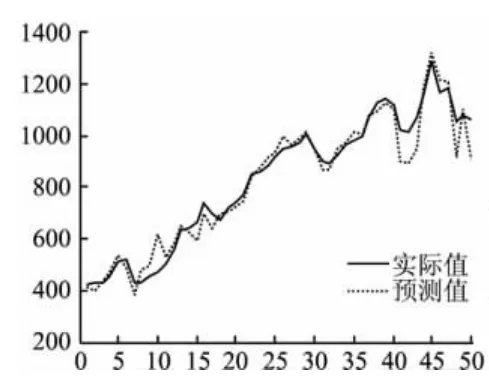
图2 小波神经网络预测结果图

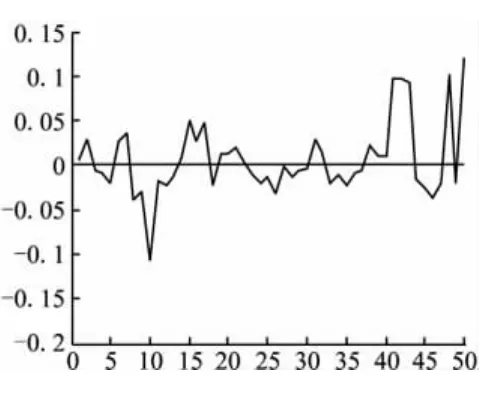
图3 小波神经网络预测误差图

由图2和图3可以看出，采用小波神经网络预测的方法对最后的50个数据进行预测，预测精度高，能够很好地满足工程需求。其中，图2表征的是风电功率预测的绝对值误差，有曲线可以看出，采用本文所述方法得到的预测曲线与实际的功率曲线吻合度很高，绝对误差的绝对值之和为1.376，反归一化后绝对误差的绝对值之和为1872.7kW，平均绝对误差为37.45kW。图3表征的是风电功率预测的相对误差曲线图，由图及原始数据可以看出，采用本方法平均相对值为2.91%，所有的数据误差均小于15%，其中，误差小于10%的数据占94%，误差小于5%的数据占86%，能够很好的满足预测的需求。这也验证了程序的正确性及有效性。

5 结论

本文通过建立小波神经网络，对风电功率进行预测，仿真结果表明:所有的预测数据与实际数据的相对误差均在15%以内，其中有94%的数据误差在10%以内。该方法能够很好地满足预测精度的需求。

风电输出预测作为其中一个重要的环节具有重要的意义，在未来的研究中，风电功率预测仍然是研究的重点和热点。本文从仿真的角度对风电功率预测进行初步研究，可以利用实时天气预报、地理信息等资源，组合预测技术等方法进行进一步研究，以提高预测精度，利于提前做好调度计划，利于电力系统稳定，提高风电的经济效益和社会效益。

［1］姜绍俊.中国电力规划［M］.北京:中国电力出版社，2007，155－162.

［2］尹明，王成山，葛旭波，等.中德风电发展与比较［J］.电工技术学报，2010，25(9):157 －162.

［3］Erasmo Cadenas，Wilfrido Rivera.Short Term Wind Speed Forecasting in La Venta，Oaxaca，Mexico，Using Artificial Neural Networks［J］.Renewable Energy，2009，34(1):274 －278.

［4］刘振亚.加强建设坚强国家电网促进中国能源可持续发展［J］.电力建设，2010，27(10)，1 －3.

［5］杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究［J］.中国电机工程学报，2005，25(11):1 －5.

［6］牛东晓，曹树华，等.电力系统负荷预测技术及其应用［M］.北京:中国电力出版社，1998.

［7］吴昌友，王福林，董志贵.改进粒子群优化算法在电力负荷组合预测模型中的应用［J］.电网技术，2009，32(2):27 －30.

［8］雷明，韩崇昭，郭文艳.非线性时间序列的小波分频预测［J］.物理学报，2005，54(5):1988 －1996.

［9］王丽婕，冬雷，廖晓钟.基于小波分析的风电场短期发电功率预测［J］.中国电机学报，2009，29(28):30 －33.