基于免疫遗传算法的设备布局问题研究

梁勤欧，周晓艳

(1.浙江师范大学地理与环境科学学院，浙江金华321004;2.武汉大学资源与环境科学学院，湖北武汉430079)

设备布局问题［1］是指在制造环境中，合理安排机器设备的位置，使生产消耗达到最小，生产效益最大化。机器设备科学合理地布局至少能节省10% ～30%的物料运输费用［2］。

设备布局问题属于组合优化中的NP难题，即随着问题的规模增加，约束条件的复杂化，其求解难度迅速增加。针对设备布局问题的特点，许多学者引入各种优化算法对其进行求解，其中应用较多的是遗传算法［3－4］。

人工免疫系统(artificial immune system，AIS)是近年来兴起的一个新的智能计算方法［5］。免疫系统的记忆功能(疫苗)常被作为遗传算法种群更新中的一种机制被使用，以便改进遗传算法的性能［6］。采用免疫系统与遗传算法相结合的新算法进行设备布局问题的研究，因其吸收了两种算法的优点，在研究效率上应该比传统的遗传算法有所提高。在借鉴免疫记忆功能与信息熵相结合的免疫遗传算法［7］基础上，提出了一种改进的免疫遗传算法，并通过单行、多行机器设备布局问题的实验来验证该算法的有效性。

1 设备布局问题的数学模型

设备布局问题根据机器的不同排列方式可划分成多种类型，如单行线性排列、双行线性排列、多行线性排列和环行排列等。为研究方便，假设机器都是矩形，且机器都水平放置，下面对单行线性排列和多行线性排列设备布局问题分别建模［8］。

对于单行机器设备布局问题，其数学模型可以描述如下:

函数目标为最小化机器之间的必要访问次数下的总费用。n为机器数;fij为机器间访问频率;cij为机器间访问时每单位距离的费用;li为机器的长度;dij为机器间最小间距;xi为机器的中心线相对垂直参考线的距离。式(1)为目标函数;式(2)约束机器不重叠;式(3)保证坐标为正值。

对于多行机器设备布局问题，其数学模型可以描述如下:

函数目标为最小化机器之间的必要访问次数下的总费用。n为机器数;m为行数;fij为机器间访问频率;cij为机器间访问时每单位距离的费用;li为机器的长度;l0为两个相邻行的中心距;dij为机器间最小间距;xi为机器的中心线相对垂直参考线的距离;yi为机器的中心线相对水平参考线的距离。式(4)分配机器到不同行;式(6)保证机器不重叠;式(7)～式(9)保证一台机器只放在一行上;式(10)保证坐标为正值。

2 免疫遗传算法的改进与设备布局问题求解

2.1 免疫遗传算法的改进

基于信息熵的免疫遗传算法考虑了抗体浓度，并利用信息熵公式计算每个个体基因位置的信息熵大小，通过设定抗体浓度阈值来保证抗体的多样性。许多学者利用该算法进行了相关问题的研究，得到了不错的结果。但该算法的缺点是运行时间长，搜索速度较慢，且比较容易早熟收敛。为了克服这些缺点，采用新的简化种群选择策略，提出一种改进的免疫遗传算法。

改进的免疫遗传算法的计算过程如下:(1)初始化种群。即系统初始化为一组随机解。(2)计算所有个体的适应度，并选择适值最好的两个个体存入抗体记忆库。

(3)对种群进行遗传算法操作并产生新种群。遗传算法操作包括选择、交叉和变异等。选择操作按照抗原—抗体之间亲和力k1，抗体—抗体之间亲和力k2进行。假设有N个种群个体，则定义第i个个体被选择的概率SP(i)为:

SP(i)=a·k1i+b·k2i(12)式中，a，b∈(0，1)为调节系数。a，b 可以按照实验经验来确定。

(4)更新抗体记忆库。如果抗体记忆库未满，选择最好的两个新个体补充记忆库。如果抗体记忆库已满，选择最好的两个新个体替换抗体记忆库中最差的两个个体。

(5)产生新种群。抗体记忆库替换同等数量种群中最差个体组成新种群。

(6)达到最大迭代次数则算法停止，最优秀的个体即为最优解。否则转回第(3)步。

以上改进的免疫遗传算法最大特点是简化了种群个体的选择机制，采用了新的亲和力组合计算的步骤。其计算量比传统的基于信息熵的免疫遗传算法大大减小。

2.2 改进的免疫遗传算法求解设备布局问题

根据以上改进的免疫遗传算法，图1列出了应用该算法解决设备布局问题的简要流程。

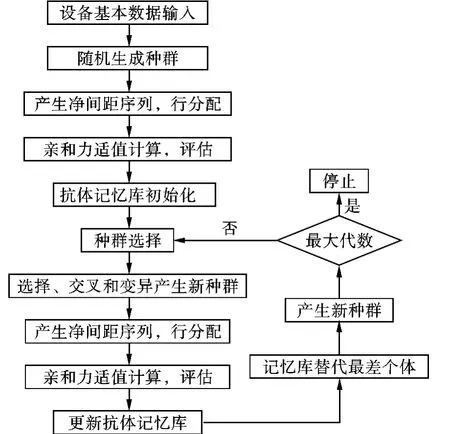
图1 改进免疫遗传算法求解设备布局问题的算法流程

(1)设备布局基本数据输入。输入的数据包括机器设备的尺寸、机器间最小距离、物流操作频率和物流操作费用等;同时也包括改进免疫遗传算法的参数初始设置，如交叉率、变异率、记忆库容量参数、迭代次数和种群个数等。

(2)随机生成种群。由于机器设备布局问题有不同的编码方式生成种群，笔者采取整数编码方案进行实验，即随机生成机器排列序列，如有6台机器，则随机排列为1到6之间的整数。

(3)产生净间距序列，进行行分配。这一步主要是针对多行机器布局而言。对于两行机器排列，首先产生初始可用空间，计算如下:

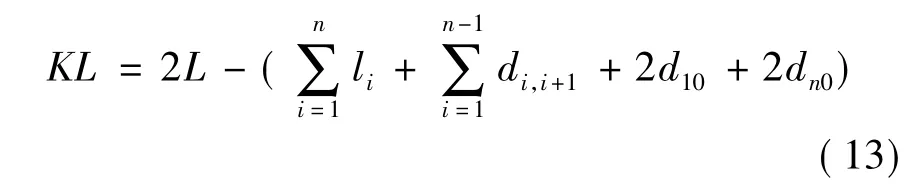
式中:KL为每个初始个体生成的可用空间;L为布局区域最大宽度;li、di，i+1分别为机器宽度和两台机器间的必需间距;d10、dn0分别为机器与布局区域边界的必需间距。

式(13)对文献［8］中的公式进行了纠正。按照文献［8］中的公式，d10、dn0是没有乘2的。但经过实验发现，如果不乘以2，对于两行机器布局初始可用空间是不成立的，因为每行机器都有一个距离区域边界的必需间距。

在计算出的初始可用空间区域内，随机生成净间距序列，生成的净间距序列之和等于可用空间长度。

机器布局行分配采取的方法是，首先依次选取机器排列及其净间距、必需间距进行总距离的计算，如果总距离没有超出L，再增加下一个紧邻机器;如果总距离超出L，则把超出的机器去除，直到总距离满足L的约束。其余机器则依次排列在下一行。

(4)亲和力适值计算与评估。在该过程中需要微调净间距序列，使得亲和力适值达到最优。微调方法是在净间距序列每一行中的任意两个不同个体分别加减一个很小的数，这个数采用可用空间与给定整数r的比值求得。如果该行净间距序列为奇数，则剩余单一的序列数不进行任何操作，循环操作次数为种群个体数与变异率的乘积。这里的净间距序列微调方法不同于文献［8］采用的交叉、变异方法，因为文献［8］的交叉方法会产生大量不可行解，原因是一般任何两个种群个体的可用净间距是不同的，交叉后常出现净间距序列和超出可用净间距的现象。

每一次净间距序列微调后，都要计算每台机器的坐标位置，然后应用式(1)或式(5)求出机器之间的必要访问次数下的总费用，在所有微调过程中选择出最优净间距序列下的总费用，即为亲和力适值。由于采用净间距序列，因此不会产生机器重叠现象。对于机器超出布局区域的情况，采取惩罚的方法把不可行解淘汰。

由于机器设备布局问题是求总目标的最小值，为了程序设计方便，用总费用的倒数表示抗体与抗原之间的亲和力，即F=1/f，这样，程序的目标就转化为求最大值问题，不可行解惩罚为一个较小实数。

(5)抗体记忆库初始化。抗体记忆库大小是根据种群个体多少决定的，一般设定为种群大小的20%～40%。记忆库每次从种群中选择最好的两个个体进行存储。抗体记忆库初始化是结合初始化种群和净间距序列，选择抗体抗原亲和力适值最好的两个个体进行存储。

(6)种群选择。按照式(12)计算遗传操作的个体选择概率，然后采用轮盘赌的方式进行种群选择。

(7)交叉变异产生新种群。对选择出的机器排列个体采取循环交叉［9］的方法产生新的种群。在交叉产生的新种群中，再以变异率为选择机制，对每个个体进行随机点变异，产生新的种群。

(8)产生净间距序列，进行行分配。对于新种群再进行净间距序列和行分配的操作。

(9)亲和力适值计算，评估，再微调净间距序列产生最优解。

(10)更新抗体记忆库。如果抗体记忆库未满，更新补充记忆库;如果抗体记忆库已满，选择最好的两个新个体替换抗体记忆库中最差的两个个体。

(11)记忆库替代最差个体，产生新种群。抗体记忆库代替遗传操作后产生的新种群的最差个体，从而组成新的种群。

(12)如果达到设定的最大迭代次数则停止迭代。否则，在新产生的种群中重新开始选择、遗传等操作。

3 实验研究

为了便于研究结果的对比，下面选择文献［8］中的实例进行实验研究。各机器的尺寸如表1所示。fij、cij、dij分别为机器间操作频率、机器间操作费用和

对于多行布局，工作区域宽度约束为22，行间中心距离为8，d10=2，dn0=2。

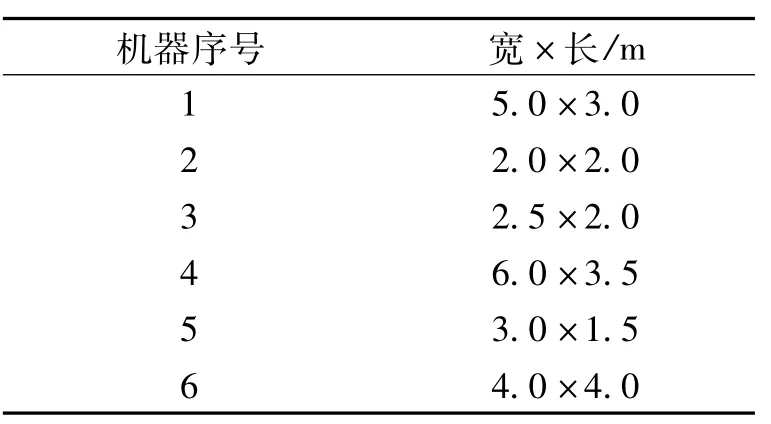
表1 机器尺寸

对于单行布局问题:初始种群数量为50;交叉率pc=0.8;变异率pm=0.3;抗体记忆库容量为 RM=20;调节系数分别为 a=0.7，b=0.2;停止迭代次数为20。

对于多行布局问题:初始种群数量为50;交叉率pc=0.8;变异率pm=0.3;抗体记忆库容量为 RM=20;调节系数分别为 a=0.7，b=0.2;停止迭代次数为100。文献［8］采用遗传算法进行求解，初始种群数量为20，交叉率pc=0.4;变异率pm=0.4;迭代次数为500。

图2为改进免疫遗传算法求解机器设备布局适值变化。图3为机器布局的实验结果。表2列出了多行机器设备布局的5个随机实验结果和文献［8］的实验值。

图2 改进免疫遗传算法求解机器设备布局适值变化

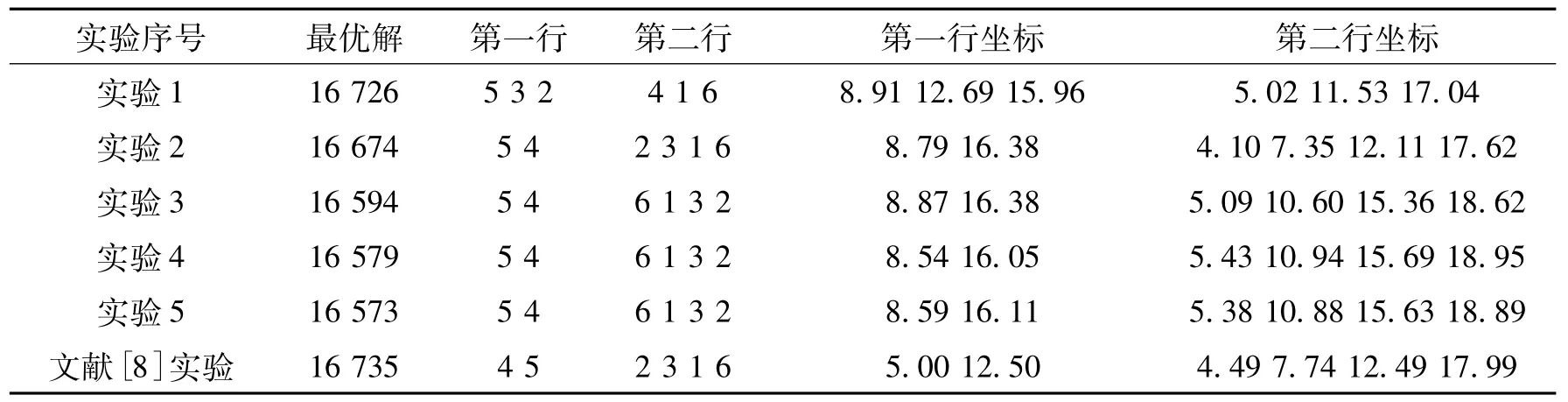
表2 多行机器设备布局实验结果

图3 机器布局的实验结果

对于单行机器设备布局实验，计算结果和文献［8］相同，最优适值为19 531，且在第2代就收敛，如图2(a)所示，机器排列序列如图3(a)所示。

对于多行机器设备布局实验，文献［8］计算结果为16 735。而表2实验结果表明，应用改进免疫遗传算法求得的结果都小于16 735，最小值达到16 573。实验1结果还搜索到每行排列3台机器的一个优秀解。每行3台机器排列的最优解由于数量少，其搜索难度较大。从图2(b)可以看出，最优解搜索是比较稳定的。综合以上说明免疫遗传算法在进行多行机器设备布局研究中是有效的。图3(b)为最优实验结果的机器排列序列图。

4 结论

人工免疫系统作为一种新兴算法，还有许多待研究的问题［10］，其应用领域也需要进一步拓宽。对机器设备布局这个组合优化难题进行了实验研究，说明了人工免疫系统算法的明显优势。下一步的研究工作将在大规模组合优化问题的实验中展开，并把人工免疫系统模型拓展应用到其他设施规划问题中。

［1］KUSIAK A，HERAGU S.The facility layout problem［J］.European Journal of Operational Research，1987，29(3):229－251.

［2］MARCELLOB，SIMONE Z，LUCIO Z.Layoutdesign in dynamic environments:strategies and quantitative indices［J］.International Journal of Production Research，2003，41(5):995 －1016.

［3］常建娥，马立坤.基于GA的计算机辅助车间设备布局设计［J］.武汉理工大学学报:信息与管理工程版，2008，30(4):548 －550.

［4］阎长罡，曹战.基于遗传算法的车间设备布局设计［J］.大连交通大学学报，2007，9(3):33 －37.

［5］DE CASTRO LN，VON ZUBEN F J.Artificial immune systems:basic theory and applications［R］.Campinas:State University of Campinas，1999.

［6］焦李成，杜海峰.免疫优化计算、学习与识别［M］.北京:科学出版社，2006:59－90.

［7］CHUN J，KIM M，JUN H.Shape optimization of electromagnetic devices using immune algorithm［J］.IEEE Transactions on Magnetics，1997，33(2):1876 －1879.

［8］玄光男，程润伟.遗传算法与工程设计［M］.北京:科学出版社，2000:208－219.

［9］OLIVER IM，SMITH D J，HOLLAND JR C.A study of permutation crossover operators on the traveling salesman problem［C］//Proceedings of the second international conference on genetic algorithm.New Jersey: ［s.n.］，1987:224 －230.

［10］TIMMIS JA，HONE T S，CLARK E.Theoretical advances in artificial immune systems［J］.Theoretical Computer Science，2008，403(1):11 －32.