考虑共同作用的刚性桩复合地基解析分析及其工程应用*

2011-07-24李希平陈存恩倪光乐陶龙光

中山大学学报(自然科学版)(中英文) 2011年2期

李希平，陈存恩，刘波，倪光乐，陶龙光

(1. 中国矿业大学(北京)力学与建筑工程学院，北京 1000832. 广州市城乡建设委员会，广东广州 510032；3. 华南农业大学水利与土木工程学院，广东广州 510642；4. 广州市泰基工程技术有限公司，广东广州 510507)

随着刚性桩复合地基在我国应用的逐渐增多，刚性桩复合地基共同作用的研究已经成为岩土工程界研究较多的领域之一，其研究方法除了采用试验方法之外[1-3]，理论分析则以数值方法为主[4-6]，主要是有限元法与边界元方法。数值方法适用性强，单元划分较为方便，但是在处理地基土为半无限空间时显得较为困难，傅景辉等[7-9]提出了简化的共同作用解析分析方法，由于把桩和土体简单地当作压缩杆件，因此，其计算方法在理论上存在仍需完善之处。从陆培炎[10]、倪光乐等[11-13]提出地基基础共同作用半解析半数值方法以来，由于采用的理论对地基、基础等的计算都是精确的解析解，并与数值方法相结合，在处理一些地基基础共同作用问题上具有计算速度快、精度高等优点，因此，近年来，在工程应用上越来越多。

本文在有关地基基础共同作用的研究成果基础上，通过离散，将刚性桩复合地基看成为桩、筏板、垫层以及地基的共同作用，考虑复合地基中桩、土、筏板和垫层之间的内力平衡和变形协调，建立复合地基共同作用的半解析半数值分析方法。本文还将以上的方法应用于工程实例分析，并通过现场实测来检验计算结果的可靠性。

1 刚性桩复合地基共同作用分析模型

对于如图1(a)所示的刚性桩复合地基系统，可以通过离散，将(a)分解为(b)、(c)、(d)、(e)所示的筏板、垫层、桩、地基4个受力体，同时它们相互之间满足内力平衡和变形协调。

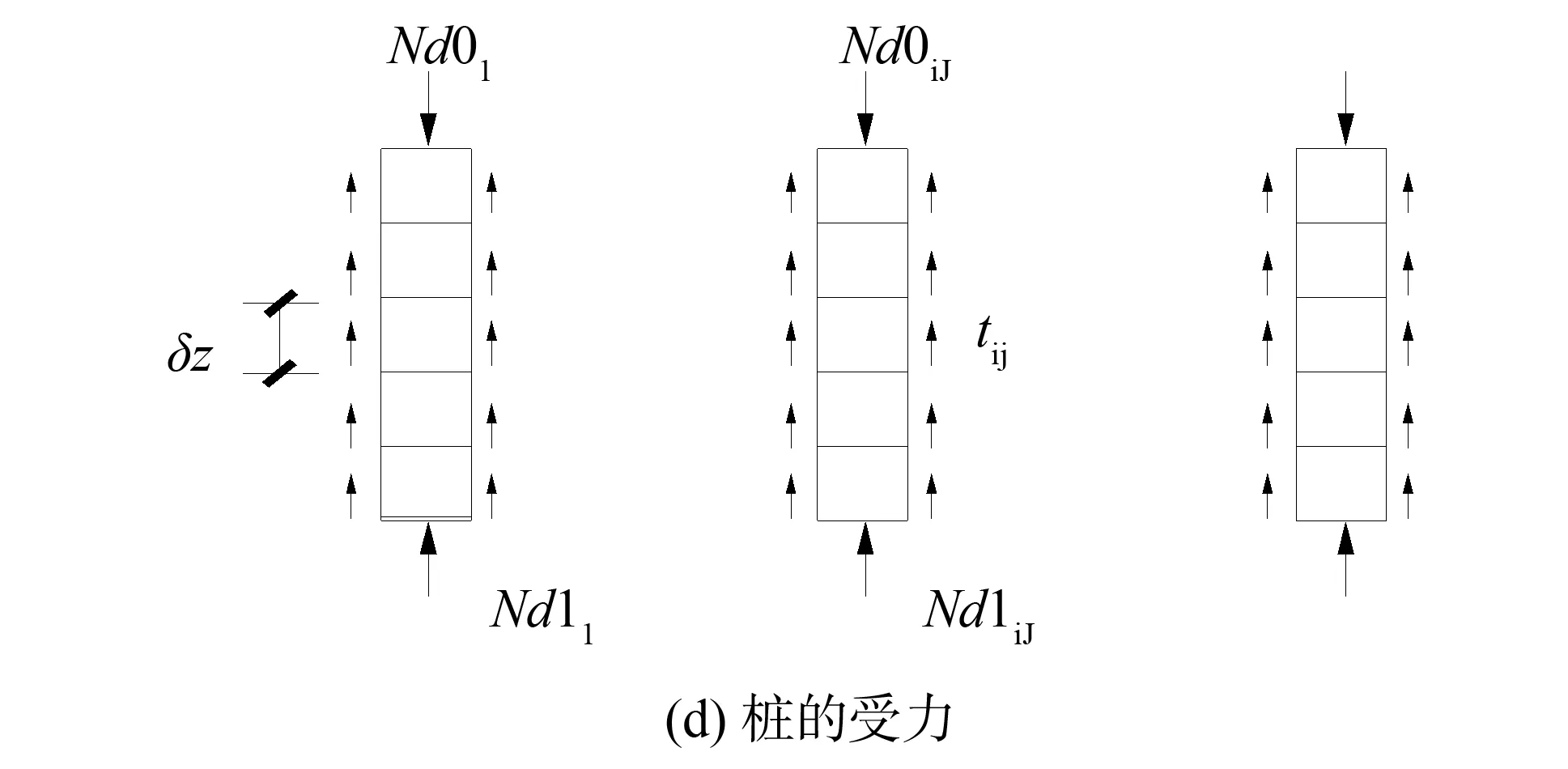
图1 复合地基系统分解离散

1.1 弹性半空间模型Mindlin解

如图2所示，竖向集中力作用于半空间内部一点(0,0,+c)时，在半空间任意点(x,y,z)处产生的沉降为[14]：

(1)

图2 竖向集中力作用下空间某点示意图

由式(1)，当荷载作用在任意点(ξ,η,ζ)时，在半空间任意点M(x,y,z)处产生的沉降为：

(2)

式中：μ为土的泊松比，R1、R2为与力作用点和所求点相关的函数，可表示为：

对于刚性桩复合地基，桩体在大多情况下为圆形，因此，在应用土的Mindlin解时需要在圆形区域上进行积分。如图3所示，对式(2)积分得到在埋深为c的单位桩端阻力作用下的土中任一点M(ρ,θ,z)产生的沉降w(ρ,z,c)：

(3)

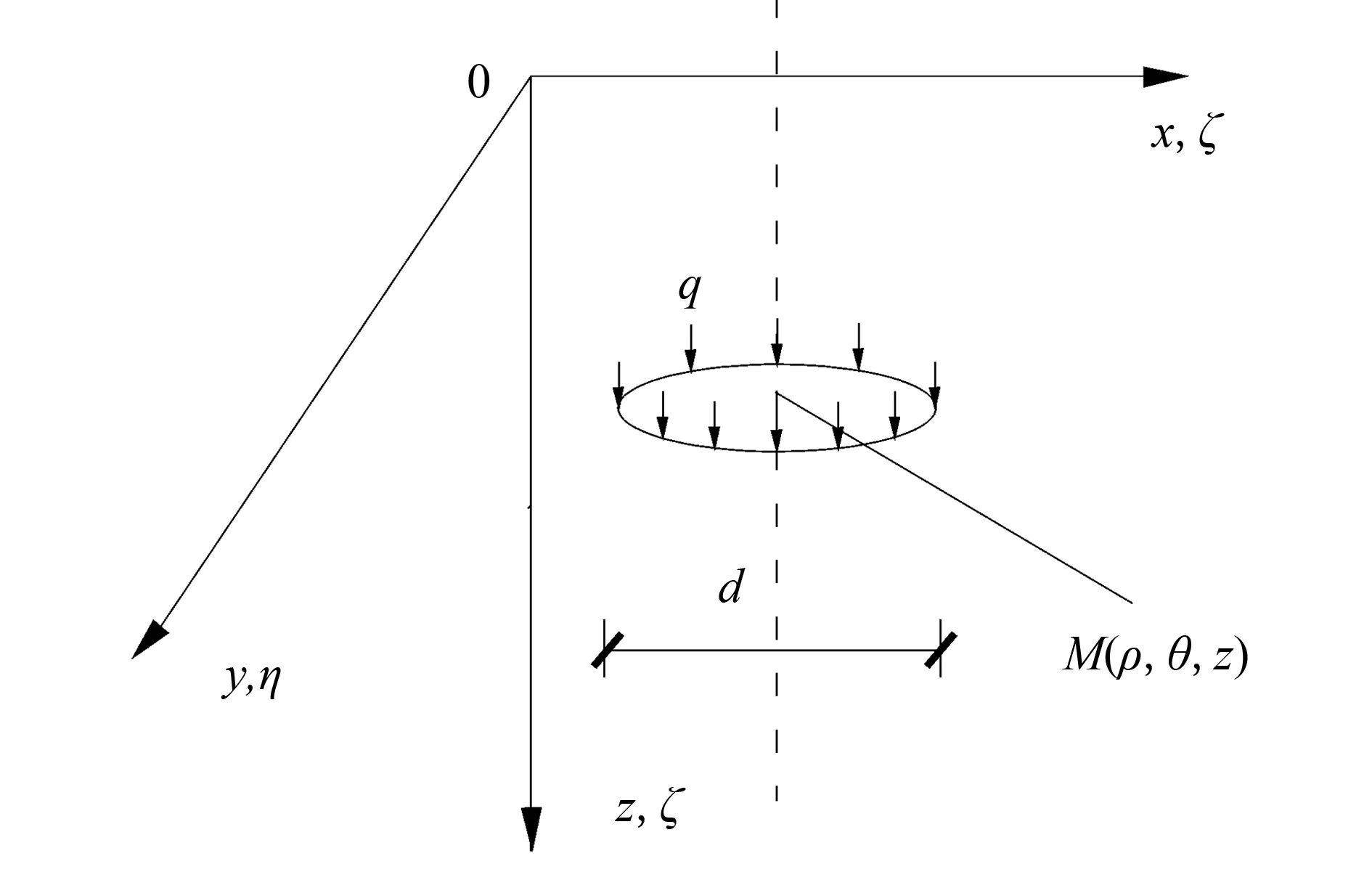
图3 竖向均布荷载作用在圆形面积上

为了求得如图4所示在桩周摩擦力τ作用下土体的位移，通过对(2)式积分就可得到柱面上端埋深为ζ1、柱面下端埋深为ζ2的柱面上，分布有单位柱面均布荷载的情况下，土中任一点M(ρ,θ,z)产生的沉降w(ρ,z,ζ1,ζ2)：

图4 竖向环形荷载计算模型

(4)

1.2 弹性地基上四周自由矩形板弹性理论解

弹性地基上的四周自由矩形板，在荷载作用下的位移解可以由文[11]的叠加方法得到，包括以下3部分。

1)在板内ξ(2-ξ1)×(η2-η1)面积上受到局部均布力q作用时四边简支矩形板的解为

(5)

式中：

2)地基上四边简支矩形板受地基反力作用时的位移解

第j网格单位地基反力X作用下板的位移为

(6)

式中：

ξxj、ηxj、δξxj、δηxj为X作用中心点坐标和长宽尺寸。

(7)

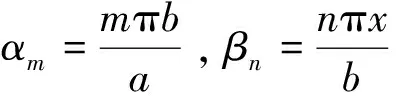
同理，在y=b，x=0，x=a边广义简支，另三边简支的解分别为：

(8)

(9)

(10)

于是有

(11)

板的总变形为

(12)

1.3 刚性桩复合地基共同作用分析模型

对于图1所示的刚性桩复合地基离散后，各部分之间的内力平衡和变形协调包括以下几部分：

1)筏板与地基位移协调。

-w(xi,yi)(i=1,2,…nn)

(13)

2)筏板的平衡。

(14)

式中：xi,yi为网格中心坐标，Δ,α,β分别为基础板的角点刚体位移以及两个方向绕角点的转角，∑FZ，∑Mx，∑My为基础板面所受的外力及两个方向的弯矩。

3)垫层的变形。

垫层在桩顶反力作用下产生压缩变形为：

(15)

4)桩与地基的位移协调。

第iJ根桩在桩顶反力Nd0iJ、桩底反力Nd1iJ与桩侧摩阻力τiJ共同作用下，对于均质地基，第iJ根桩顶沉降为：

(16)

式中：E,Es分别为桩、土的弹性模量，A、A1为桩身和扩大头直径。

如果地基是分层的，则τiJ在每层都是不相同的，那么式(16)中与τiJ有关的第二项可通过分层求和的方法求得。

而与桩接触处土体的位移可以按叠加方法计算得到，假定桩体的存在不影响地基沉降的计算，按照图1(e)的荷载分布，就可以计算土体位移，令桩土位移相等或满足某接触模型就可建立桩土位移协调方程。

5)筏板与桩的位移协调。

筏板的位移为

SZ(x,y)=Δ+xtgα+ytgβ-w(x,y)

(17)

筏板在第iJ根桩对应的位置的位移为：

SZ(xJiJ,yJiJ)=Δ+xJiJtgα+yJiJtgβ-

Nd0jJ-wq(xJiJ,yJiJ)

(18)

筏板的位移与第iJ根桩的桩顶位移SJiJ之差等于垫层的压缩量δΔHiJ，即

SZ(xJiJ,yJiJ)-SJiJ=δΔHiJ

(19)

6)基础板四边自由边界条件方程。

地基上的四边自由板必须满足四边剪力为零的边界条件，按照剪力计算公式

(20)

地基板在荷载作用下产生的板边剪力包括以下3部分：

Ⅰ)板面荷载q作用下在y=0边产生的剪力为(取级数的前N项)：

(21)

同理，板面荷载q作用下在y=b，x=0，x=a边产生的剪力为：

(22)

Ⅱ) 地基反力X作用下板边剪力为：

(23)

Ⅲ)板边广义位移在y=0，y=b，x=0，x=a四条边产生的剪力为：

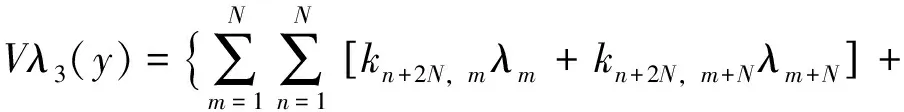
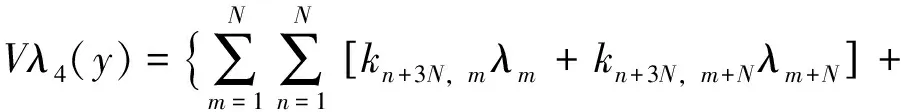
(24)

式中：

对由方程(21)-(24)得到的板边剪力，令所有荷载作用下在y=0，y=b,x=0，x=a边剪力之和为零，可以分别得到四边剪力为零的平衡方程：

(25)

联立以上的方程(13)-(16)、(19)、(25)，就可以得到刚性桩复合地基共同作用整体方程组，也即刚性桩复合地基共同作用的半解析半数值解。

2 工程实例分析

本文选取广东省东莞市某商业中心项目来说明该方法的具体应用。该大厦楼高23层，采用筏板基础与刚性桩复合地基，筏板厚h=1.6 m，砼弹性模量E=30 000 MPa，泊松比μ=1/6。考虑桩、桩间土、筏板共同作用，按每层16 kN/m2的荷载值进行计算。板下垫层厚ΔH=20 cm，变形模量E=35 MPa。垫层下面的桩布置如图5所示，桩径d=1.7～2.1 m，桩长L=9.5～14.8 m，桩身砼弹性模量为E=30 000 MPa。场地地质资料参数如图6所示。

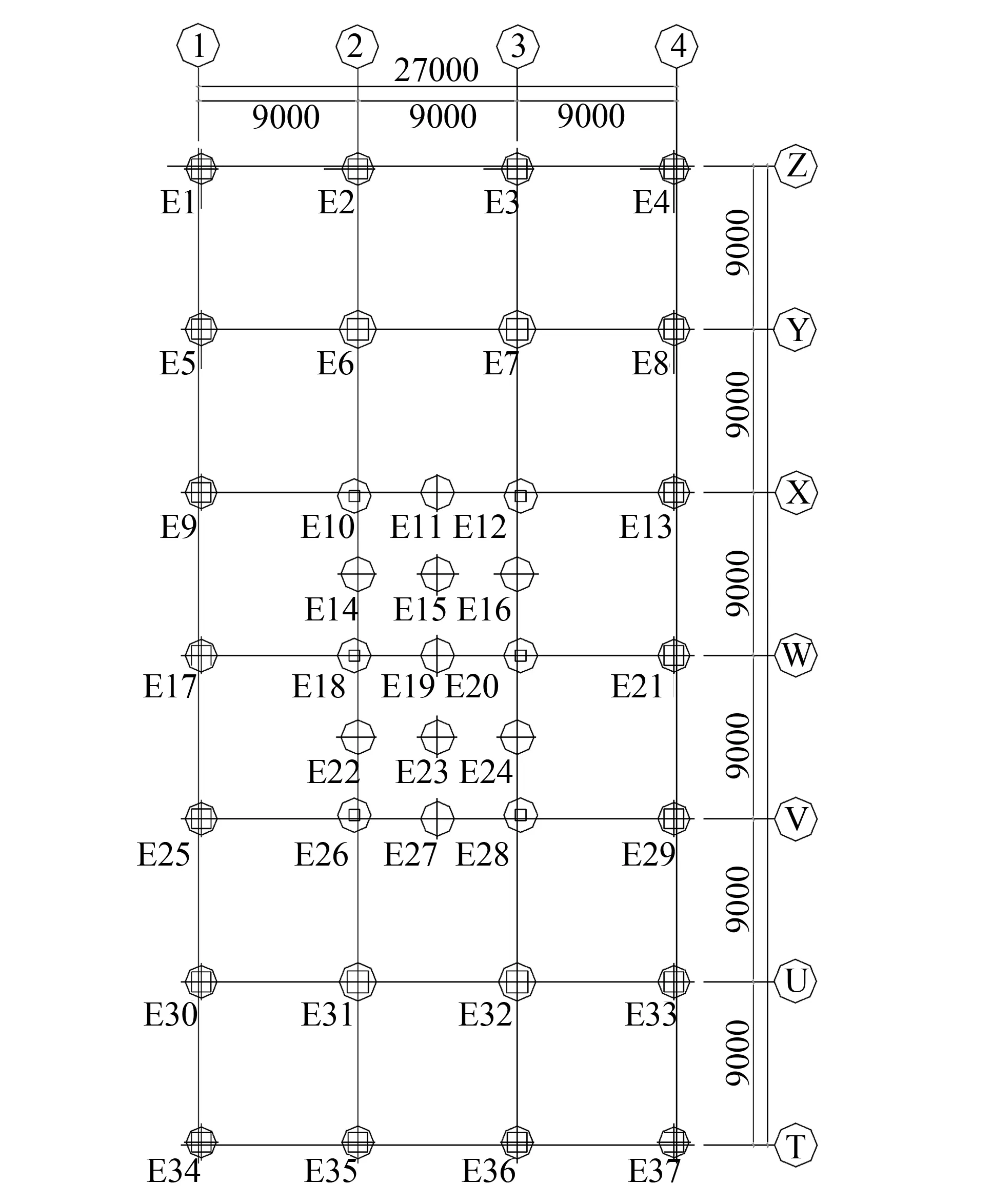
图5 桩平面布置图(mm)

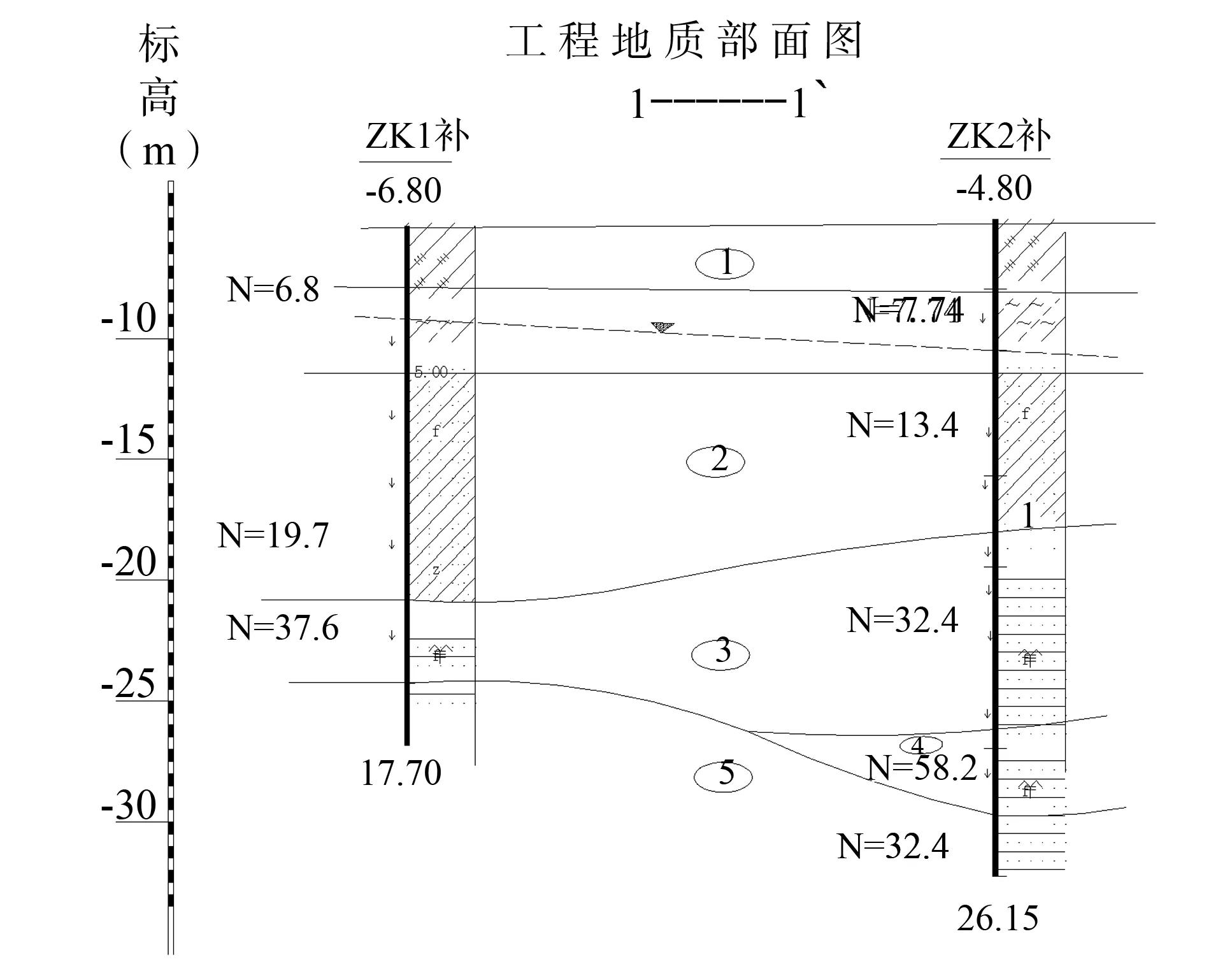
图6 工程地质剖面图

将筏板划分成x×y=16×8=128个网格单元，取计算级数项N=25。利用这些数据以及筏板和地基参数、荷载数据，输入由本文方法用Mathcad编译的计算程序，得到桩顶反力和筏板基础的沉降等，其结果如表1、表2所示。

为了检验本文方法在实际工程中的应用效果，笔者对本项目还进行了现场实地监测，监测得到的桩顶反力、基础沉降分别如图7、图8所示。

表1 桩顶反力

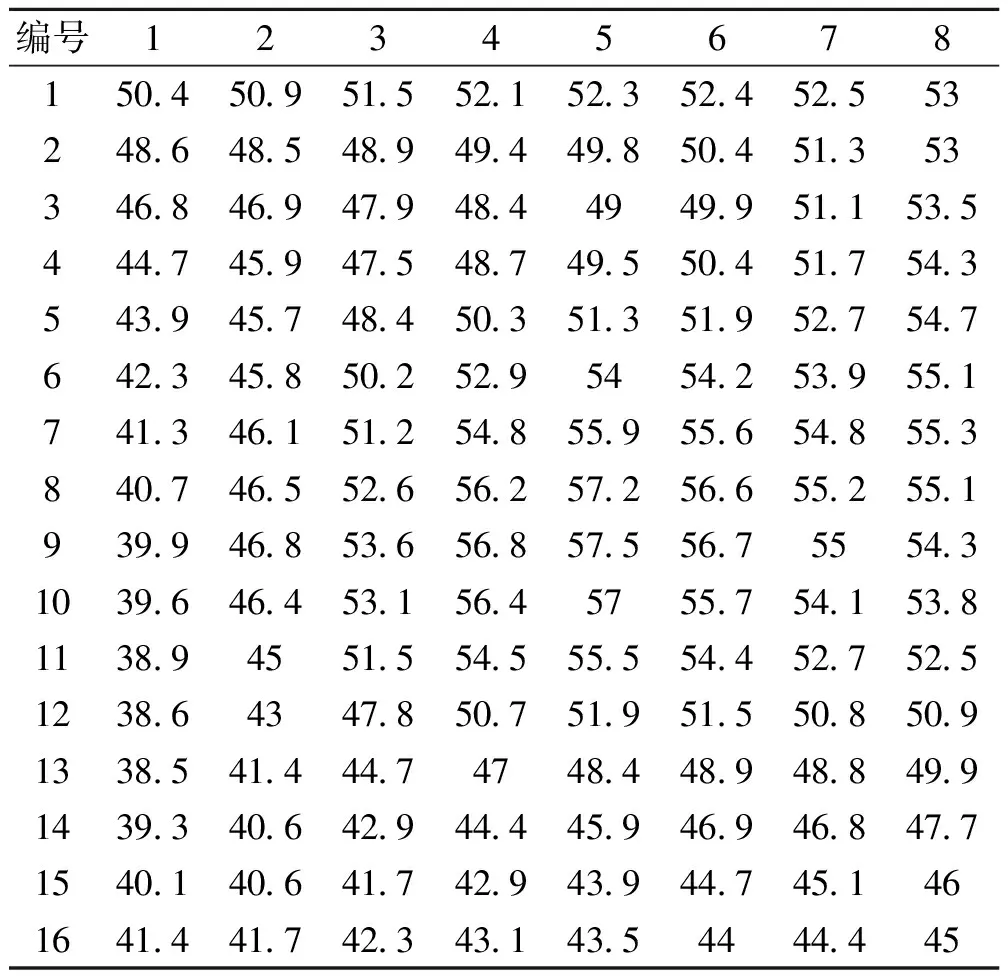
表2 筏板沉降

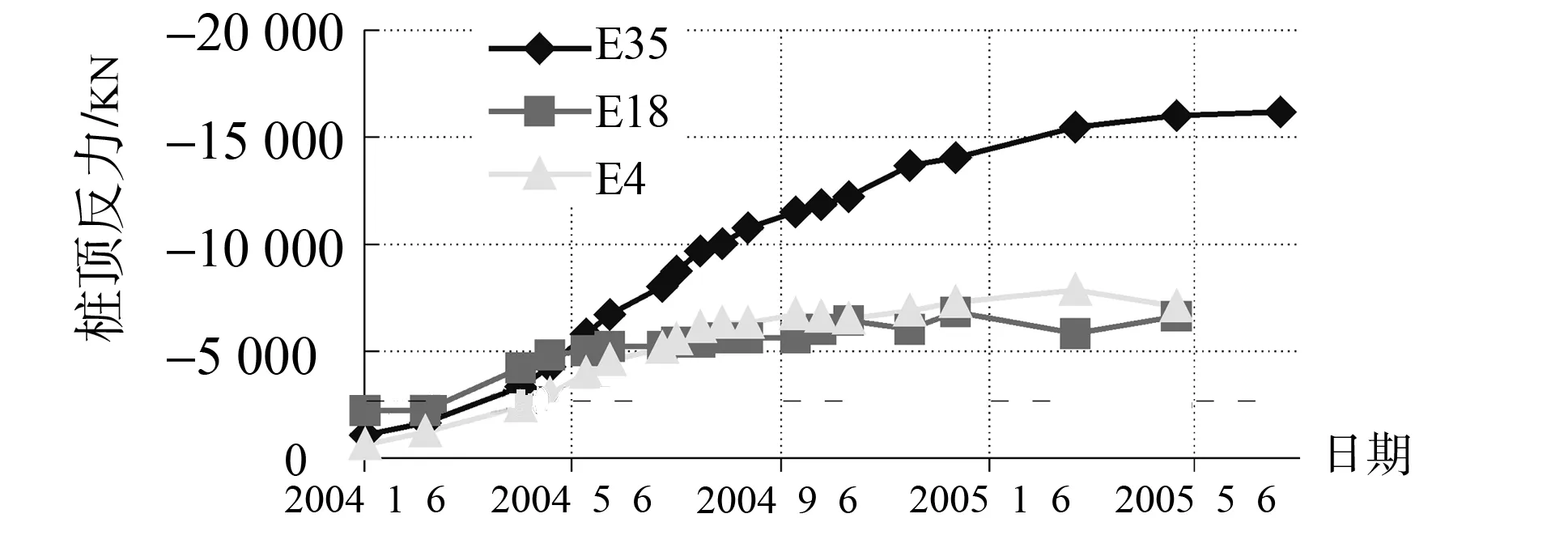
图7 桩顶反力

图8 基础沉降

以上的计算结果与实测情况表明：

1)至2005年5月6日，此时E35，E18 ，E4三条桩的承载荷载分别为16 185 kN、6 609 kN、7 081 kN，而E35，E18 ，E4理论计算承载力分别为10 835 kN、8 491 kN、7 008 kN。可见桩顶反力分布与计算结果分布规律相似，计算结果与实侧结果也是相近的。

2)实测平均沉降为62 mm，理论计算平均沉降约为50 mm，可见计算结果较好的反映了实际情况。