相对论平均场理论中耦合常数gρ的确定与研究*
2011-07-24赵先锋
赵先锋
(滁州学院电子信息工程系,安徽 滁州 239000)
在包括σ,ω,ρ介子及σ介子自相互作用的相对论平均场理论(RMF)中,需要确定核子与介子的耦合常数。 近些年来,在相对论平均场理论的研究中,人们得到了多组介子与核子的耦合参数,如NL3、TM1、TM2、NLSH、GL85和GL97等[1-5]。这五个耦合常数中,其中的gρ是描述无限核物质中质子和中子的不对称性质的,它联系于饱和核物质的密度ρ0、有效质量m*,尤其是对称能量系数asym[5]。由于实验核物理的不断发展,对于饱和核物质对称能的研究乃是一个非常活跃的领域。
对称能的研究可以通过多种实验方法进行,其中最重要的一种是通过重离子碰撞获得相关数据[6-15]。2004年,Tsang等[16]在美国密歇根州立大学的国家超导回旋加速器实验室(NSCL/MSU)进行了112Sn和114Sn的重离子碰撞试验,给出了较新的对称能实验数据。
本文从相对论平均场理论出发,导出ρ介子与核子的耦合参数gρ的代数关系式; 并对相对论平均场理论计算中曾用到的几组ρ介子耦合参数进行分析;采用NSCL/MSU给出的核子最新实验数据,对ρ介子与核子的耦合参数gρ进行计算并对结果进行讨论。
1 耦合常数gρ代数表达式的推导
核物质的拉格朗日密度为[5]
(1)
式中,Ψ是核子的Dirac旋量,对应的质量为m。σ,ω,ρ分别是σ介子、ω介子和ρ介子的场算符,mσ,mω,mρ是这些介子的质量.gσ,gω,gρ,g2,g3为核子耦合常数,它们可以利用饱和核物质的性质,如密度ρ0、束缚能B/A、压缩系数K、有效质量m*和对称能量系数asym定出。
对于核物质,应用相对论平均场近似后,得到由中子和质子非对称性所贡献的能量密度为[5]
(2)
式中k为核子的费米动量。
令核物质核子数密度为ρ,中子数密度为ρn,质子数密度为ρp,则有
ρ=ρn+ρp
(3)
再令
t=(ρn-ρp)
(4)
利用ρ介子的平均值方程
(5)
则有
(6)
故由中子和质子非对称性所贡献的单个核子能量密度为
(7)
利用积分公式
并令核子有效质量为
m*=m-gσσ
(8)
则(7)式积分后化为
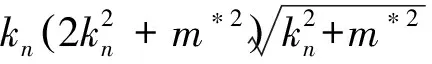
(9)
对称能系数为单核子能量对t的二阶偏导数
(10)
易求
(11)
为了计算(9)式后面几项对t的二阶偏导,令
(12)
联立(3)、(4)式得
(13)
费米动量和饱和核密度的关系是
(14)
把(14)式代入(13)式,得
(15)
所以,
(16)
由此,得
(17)
由(15)式可知,t=0即意味着kn=kp=kF,因此
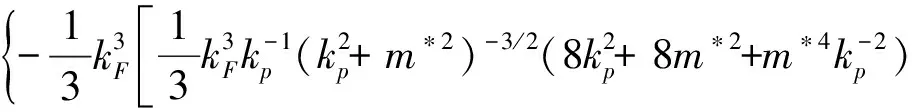
(18)
同理可得,
(19)
又因为
(20)
所以
(21)
同理,
(22)
把(9)、(11)、(18)、(19)、(21)和(22)式代入(10)式,得对称能系数为
(23)
由此得ρ介子的耦合参数为
(24)
由(14)式,上式亦可写为
(25)
式(24)、(25)即为计算ρ介子耦合参数的代数表达式,据此,ρ介子的耦合参数gρ可以利用饱和核物质的密度ρ0、对称能系数asym和有效质量m*给出。
按照上述公式求出的ρ介子耦合参数gρ,适用于饱和核物质;至于是否可以外推到如中子星这样的高密度物质中去,要视实验或观测数据而作相应调整。当然,把计算出的核子耦合参数应用于中子星物质时,还需要考虑到中子星物质的化学平衡条件、电中性条件和粒子数守恒条件。
2 ρ介子耦合参数的分析及新的耦合参数的计算
在相对论平均场理论的计算中,人们曾使用过多组耦合参数(见表1)。这几组数据,有的是直接由上述公式计算得出,在核物理及核天体物理的理论计算中与实验或观测结果符合得较好;有的是由上述公式算出后,其结果与实验或观测相去较远,因此,又根据有限核的单粒子性质作了相应调整[5]。

表1 相对论平均场理论计算中用过的ρ介子的耦合参数
对于耦合参数组GL97,文献[5]给出的ρ介子的耦合参数gρ数值是4.791,与我们的计算值4.794 2相符,因此,文献给出的该值是直接由计算得来的。对于耦合参数组GL85,文献[4]给出的gρ数值是6.2,与我们的计算值6.35相差2.4%,文献给出的值是直接由计算得来并作了很小调整(见图1)。
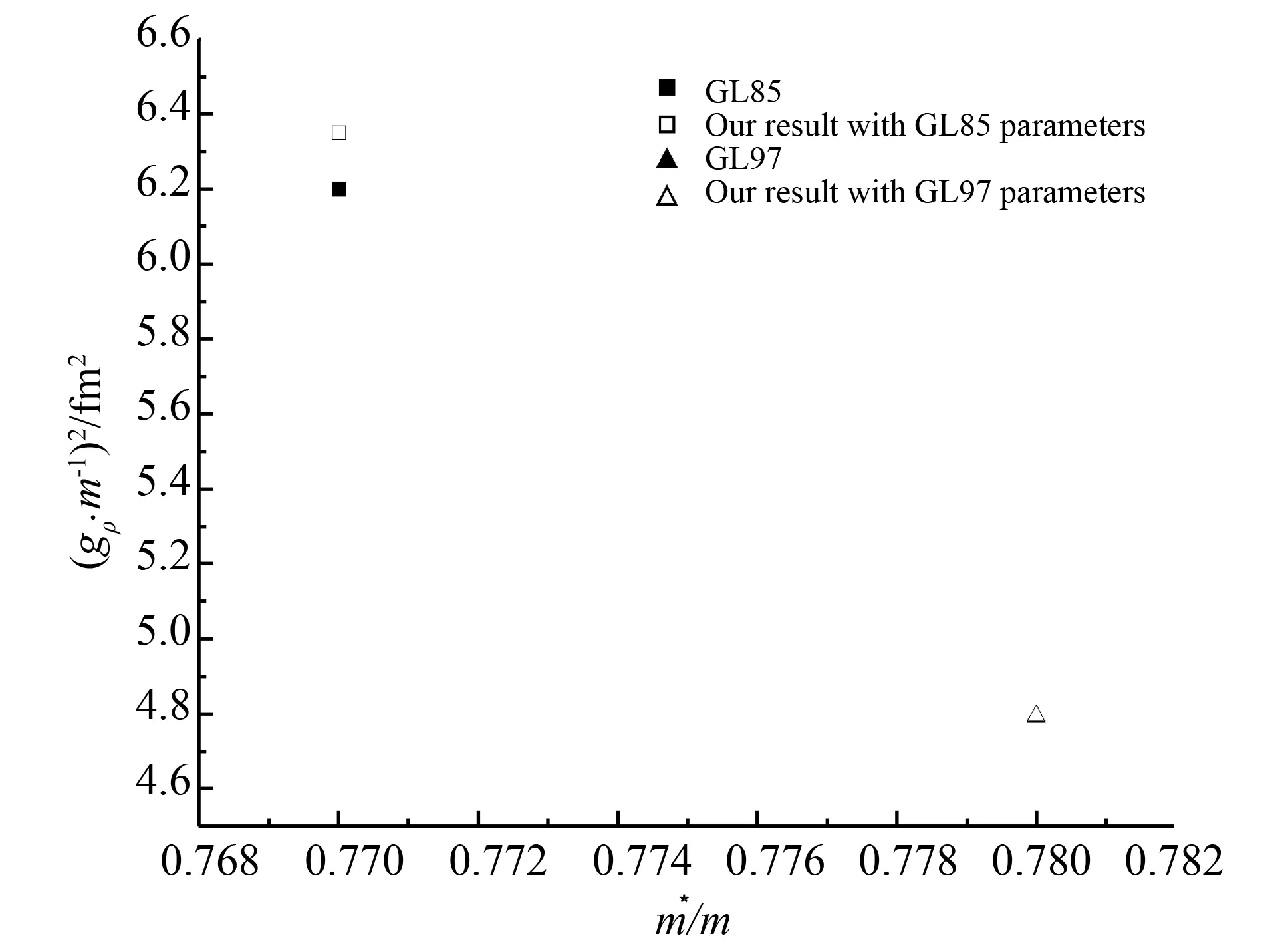
图1 耦合参数组GL97和GL85给出的gρ与本文计算值的比较
图2为耦合参数组NL3,TM1,TM2和NLSH给出的gρ值与本文计算值的比较. 由图2及表1可见,文献中给出的gρ值分别为:NL3-1.339 1,TM1-1.409 2,TM2-1.437 4,NLSH-1.284 9;而本文根据相应文献提供的核子参数计算的gρ值分别为:NL3-5.399 8,TM1-5.649 4,TM2-5.712,NLSH-5.153 4,二者相差太远. 原因是NL3和TM2适合描述轻核,TM1适合描述Z>20的重核,而NLSH仔细考虑了核的同位旋性质,适合计算远离β稳定线的核[5],直接计算值必须要利用有限核的单粒子性质作调整,才能与无限核物质和核天体物理的实验和观测结果相符。
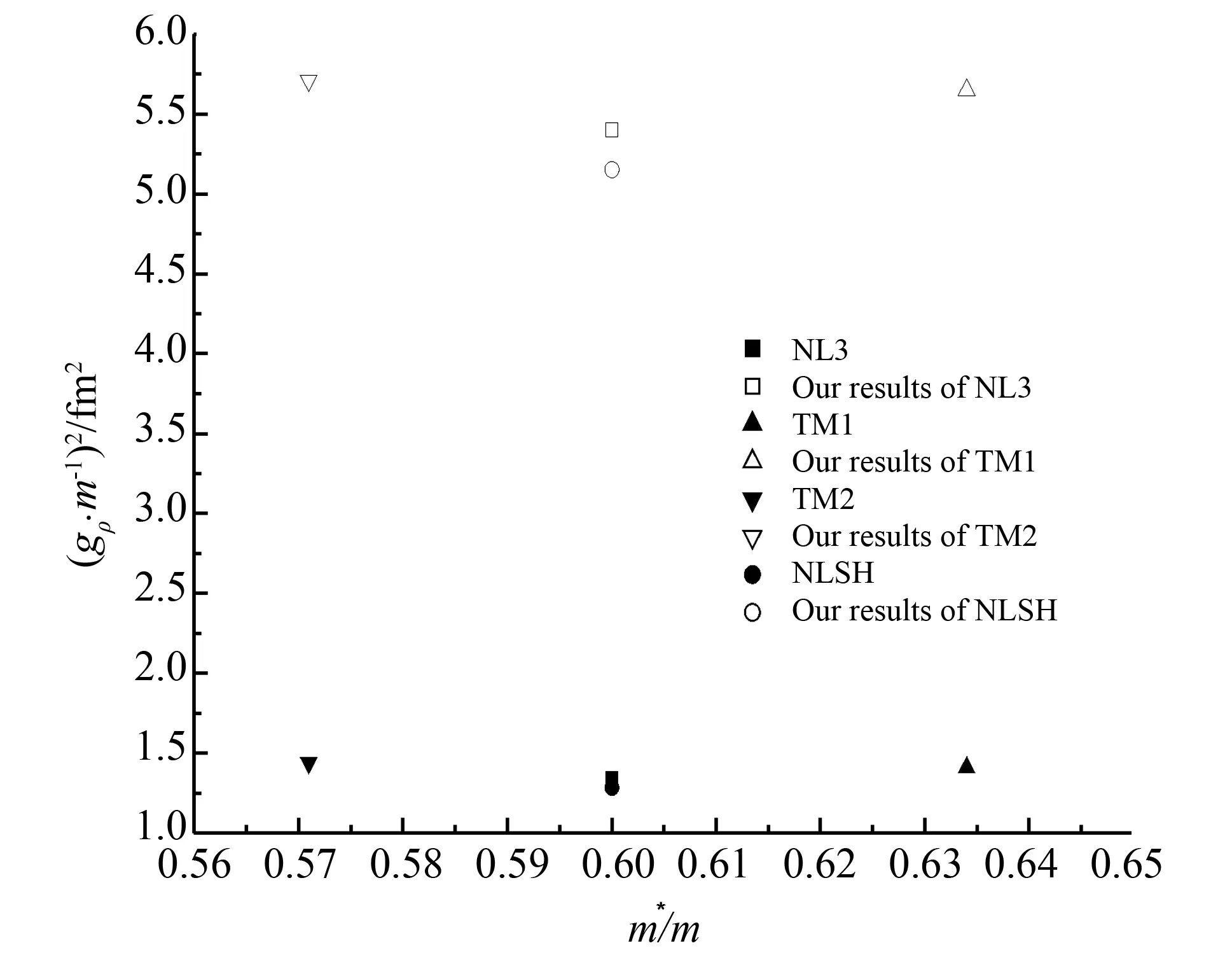
图2 耦合参数组NL3,TM1,TM2和NLSH给出的gρ与本文计算值的比较
2004年,在NSCL/MSU进行的112Sn和114Sn重离子碰撞试验给出的对称能等有关核子实验数据见表2[16]。核子有效质量,当采用MDI物态方程(the MDI EOS)时取为m*/m=0.67,当采用Skyrme拟合(the Skyrme fit)时取为m*/m=0.77。 利用NSCL/MSU实验数据计算的ρ介子的耦合参数如表2和图3,它们介于GL85、GL97与NL3、TM1、TM2和NLSH之间,此计算值是否可以外推到中子星等高密度核物质中去,是否与核物理及核天体物理的实验或观测结果符合,都需具体的理论计算与实验或观测结果来验证。如不符合,尚需对其进行适当调整。

表2 NSCL/MSU给出的核子参数及本文据此计算的ρ介子耦合参数

图3 利用NSCL/MSU重离子碰撞数据计算的ρ介子耦合参数
3 结 论
本文从相对论平均场理论出发,导出了ρ介子与核子的耦合参数gρ与饱和核物质密度ρ0、对称能量系数asym及核子有效质量m*之间的代数关系式;由得到的公式对相对论平均场理论计算中曾用到的几组ρ介子耦合参数进行了分析。 采用NSCL/MSU给出的核子最新实验数据,对ρ介子与核子的耦合参数gρ进行了计算并作了初步讨论。
参考文献:
[1]LALAZISSIS G A, KONIG J, RING P. A new parameterization for the Lagrangian density of relativistic mean field theory[J]. Phys Rev C, 1997, 55(1):540-543.
[2]SUGAHARA Y, TOKI H. Relativistic mean field theory for lambda hypernuclei and neutron stars[J]. Prog Theor Phys, 1994, 92(4):803-813.
[3]SHARMA M M,NAGARAJAN M A , RING P. Rho meson coupling in the relativistic mean field theory and description of exotic nuclei[J]. Phys Lett B, 1993, 312(4):377-381.
[4]GLENDENNING N K. Neutron stars are giant hypernuclei?[J]. Ap J, 1985,293: 470.
[5]GLENDENNING N K. Compact stars: neuclear physics,particle physics, and general relativety[M]. New York:Springer-Verlag, 1997.
[6]TSANG M B , FRIEDMAN W A , GELBKE C K, et al. Isotopic scaling in nuclear reactions[J]. Phys Rev Lett, 2001, 86(22):5023-5026.
[7]ONO A , DANIELEWICZ P, FRIEDMAN W A , et al. Isospin fractionation and isoscaling in dynamical simulations of nuclear collisions[J]. Phys Rev C, 2003, 68(5):051601.
[8]LI Bao an. Neutron-proton differential flow as a probe of isospin-dependence of the nuclear equation of state[J]. Phys Rev Lett, 2000, 85(20):4221-4224.
[9]LI Bao an. Probing the high density behaviour of nuclear symmetry[J]. Phys Rev Lett, 2002, 88:192701.
[10]CHEN Lie wen, GRECO V, KO C M, et al. Effects of symmetry energy on two-nucleon correlation functions in heavy-ion collisions induced by neutron-rich nuclei[J]. Phys Rev Lett, 2003, 90(16): 162701.
[11]TAN W P, LI Bao an , DONANGELO R, et al. Fragment isotope distributions and the isospin dependent equation of state[J]. Phys Rev C, 2001, 64(5): 051901(R).
[12]MULLER H, SEROT B D. Phase transitions in warm, asymmetric nuclear matter[J]. Phys Rev C , 1995, 52(4):2072-2091.
[13]LI Bao an, KO C M. Chemical and mechanical instability in hot isospin-asymmetric nuclear matter[J]. Nucl Phys A, 1997(618): 498-508.
[14]BARAN V, COLONNA M, TORO M D, et al. Spinodal decomposition of low-density asymmetric nuclear matter[J]. Nucl Phys A, 1998, 632(2):287-303.
[15]XU H S, TSANG M B, LIU T X, et al. Isospin fractionation in nuclear multifragmentation[J]. Phys Rev Lett, 2000, 85(4):716-719.
[16]TSANG M B, LIU T X, SHI L, et al. Isospin diffusion and the nuclear symmetry energy in heavy ion reactions[J]. Phys Rev Lett, 2004, 92(6):062701.
