脉动风场数值模拟的POD－谐波合成法

孙 瑛，林 斌，武 岳，孙晓颖

（1.哈尔滨工业大学 土木工程学院，150090 哈尔滨，sunnyhit@hit.edu.cn;2.北京市建设工程发包承包交易中心，100083 北京）

脉动风场数值模拟的POD－谐波合成法

孙 瑛1，林 斌2，武 岳1，孙晓颖1

（1.哈尔滨工业大学 土木工程学院，150090 哈尔滨，sunnyhit@hit.edu.cn;2.北京市建设工程发包承包交易中心，100083 北京）

谐波合成法(WAWS)具有较高的随机序列生成精度，是目前进行随机风场模拟中较多采用的方法，但在模拟多节点、长序列脉动风场时程时往往存在计算效率低、内存易超限的问题.本文结合谐波合成法与POD技术(WAWS/POD)，在保证计算精度的前提下大大提高计算效率，解决了数值模拟过程中计算内存超限的问题.同时为方便用户掌握数值模拟的精度，给出该方法的误差控制指标，用于选择正交分解阶数.最后，采用WAWS/POD联合法模拟了空间200个节点的脉动风场，验证了方法的准确性和高效性.

脉动风;数值模拟;本征正交分解;谐波合成法

随着现代工程结构的日趋大型化、复杂化，风致动力响应分析成为许多结构设计中必不可少的环节.当采用时程方法进行结构风致动力响应分析时通常需要先对来流脉动风场进行模拟，即使是通过多点同步测压试验获得脉动风压时程的情况，也会由于测点数的限制及与结构作用点的不同而需要进行数值模拟或插值分析.目前用于脉动风速时程模拟的方法主要有线性滤波器法(AR或ARMA)、小波变换法(DWT)和谐波合成法(WAWS)等.线性滤波器法［1－3］模拟效率较高，但属于有条件稳定的模拟方法［4］，在模拟过程中模型定阶问题具有一定的经验性，模拟精度相对较差;小波变换法［5－6］在模拟非平稳信号时具有一定的优势，但是小波基的选取以及小波系数的估计对模拟精度有较大的影响，通常情况下不建议采用该方法来模拟平稳随机过程;谐波合成法［7］将随机风速视为一系列余弦波的叠加，理论简单清晰，而且可以生成无条件稳定的高精度模拟结果，因而在随机风场模拟中应用最多.然而，谐波合成法的缺点也是明显的，即计算效率不高;特别是当模拟的空间点数较多时，互谱密度矩阵中元素的生成和矩阵的分解工作量都将大大增加，同时谐波项的叠加过程也会耗费大量的计算时间，而且很有可能会出现计算内存超限的问题.针对谐波合成法计算效率低、计算消耗大的问题，国内外学者已开展了一些研究［8－11］.Yang［8］将快速傅里叶变换(FFT)技术应用到模拟算法中，使谐波项的叠加效率有了很大提高;曹映泓等［10］提出采用互谱密度矩阵Cholesky分解的显示表达式和忽略部分余弦项来提高计算效率，但通常情况下无法获得Cholesky分解的显示表达式，而且在忽略余弦项时没有一个明显的误差控制指标，因此该方法在实际使用中受到一定限制;罗俊杰等［11］提出采用递归优化算法进行矩阵的Cholesky分解，同时引入矩阵乘算法来提高计算效率.尽管这些研究工作对谐波合成法有所改进，但都存在计算效率低下的问题，因此仍需要从算法出发寻求更为有效的改进技术，以实现在有限的计算资源上获得理想结果.

本文在对谐波合成法进行深入剖析的基础上，通过引入随机场的高效描述方法——本征正交分解技术(POD)，与谐波合成法相结合，在保证计算精度的前提下大大提高计算效率，解决了数值模拟过程中计算内存超限的问题，同时在模拟中运用快速傅里叶变化技术以简化计算过程，提高了计算速度;此外，给出该方法的误差控制指标，用于选择正交分解的阶数;最后，采用WAWS/POD联合法模拟了空间200个节点的脉动风场，验证了方法的准确性和高效性.

1 谐波合成法

根据 Shinozuka理论［7］，对一维、n变量、零均值的高斯随机过程{V(t)}可由下式来模拟

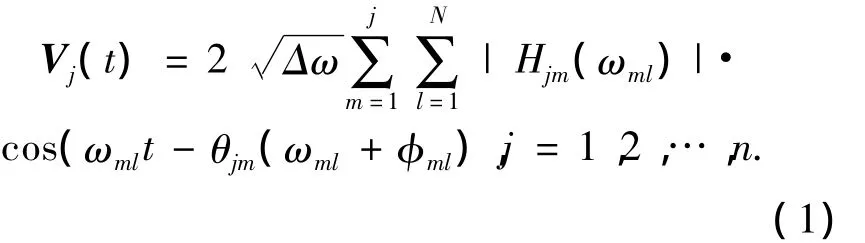
式中:j为需要模拟的空间场点数，N为频率等份数，是一个充分大的正整数，Δω=ωup/N，为频率增量，ωup为截止频率，即当ω＞ωup时，随机过程{V(t)}的互谱密度矩阵［S0(ω)］=0，φml为均匀分布于(0，2π)区间的随机相位，Hjm(ωml)是矩阵［H(ω)］中的元素，［H(ω)］是［S0(ω)］的Cholesky分解，θjm(ω)为 Hjm(ω)的复角.可以证明，当N→∞时，式(1)模拟的随机过程满足目标谱［7，9］.

可以看出谐波合成法计算效率低的主要原因有两方面:①谐波项的叠加过程需要耗费大量计算时间;②对应每个频率都要进行互谱密度矩阵的Cholesky分解，并且随着模拟节点数目(n)的增多，计算量将按n2/2的比率增加.针对以上问题，本文对谐波合成法做了两方面的改进:

1)引入FFT技术，将随机过程模拟式(1)改写成如下表达形式［9］

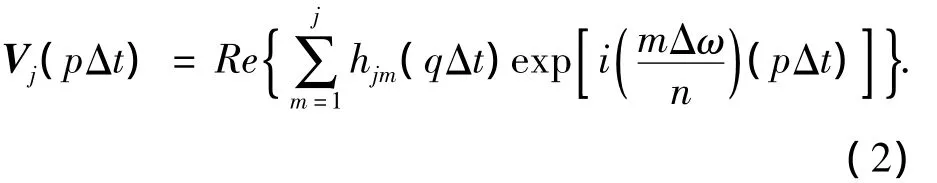
式中:p=0，1，2…M × n －1;M=2N，q是p/M的余数，q=0，1，2…M － 1.

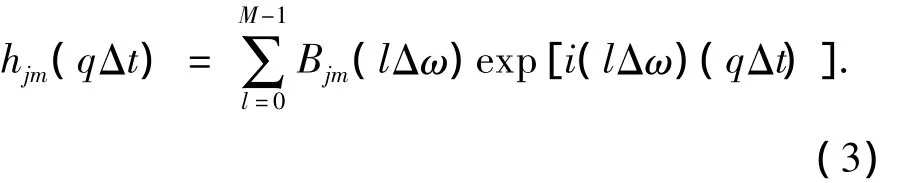
而Bjm(lΔω)的值可以通过下式确定

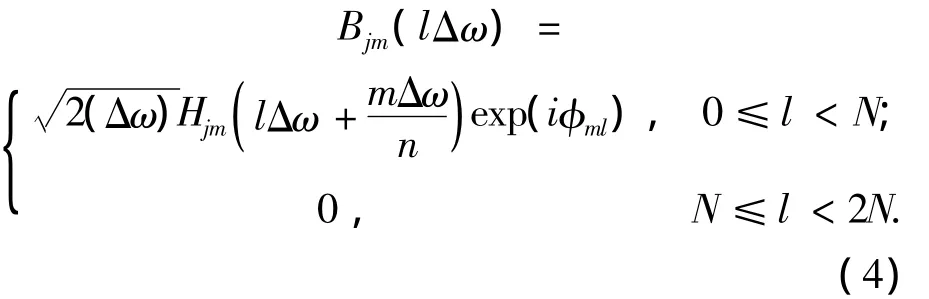
2)引入本征正交分解法(POD)，降低互谱密度矩阵的维数以提高谐波合成法的计算效率.

2 WAWS/POD联合法

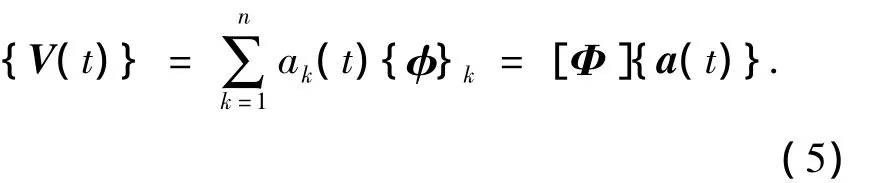
其中 {a(t)}= ［a1(t)，a2(t)，…，an(t)］T是相互正交的时间主坐标，可表示为

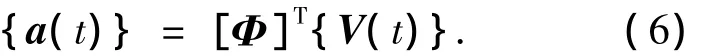
［Φ］=［{φ}1，…，{φ}n］是协方差矩阵［Cv］的本征向量(或称本征模态)矩阵，具体可由下式得到

2.1 本征正交分解法

本征正交分解法(POD)是一种随机场的高效描述方法，仅需用少量的项数就可很好描述随机场本身［12－13］.在模拟随机风场时，用低阶互谱密度矩阵代替完整互谱密度矩阵来实现降阶的目的，关键是如何确定阶数及降阶后的互谱表达式.

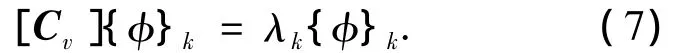
其中λk(λn≤…≤…≤λ1)是相应的本征值，它的数值大小直接反映了相应本征模态包含能量的大小.而协方差矩阵［Cv］可表示为

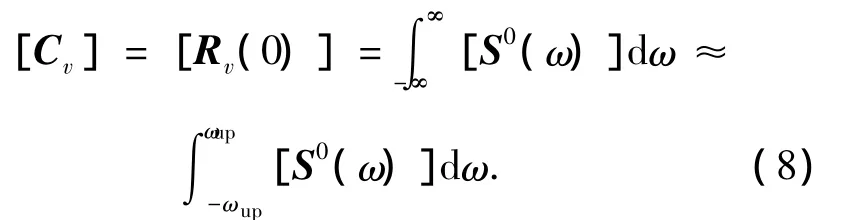
由式 (7)、(8)可得

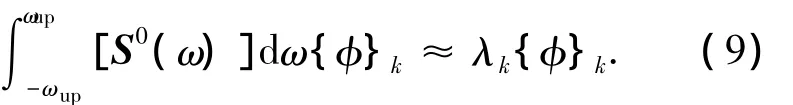
上式表明可由随机过程的互谱密度矩阵近似得到协方差矩阵［Cv］的本征模态矩阵［Φ］，时间主坐标{a(t)}的互谱密度矩阵［S0a(ω)］为

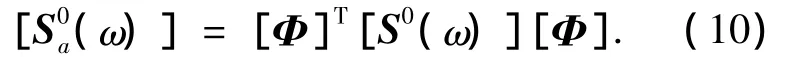
式(9)、(10)表明，可通过随机过程{V(t)}的互谱密度矩阵来近似获得时间主坐标{a(t)}的互谱密度矩阵.另外，根据POD原理，an(t)的均方值即本征值λn.

2.2 WAWS/POD联合法的提出

首先通过引入本征正交分解法(POD)，来获得能够近似代表实际风场频谱特性的少量阶时间主坐标的互谱密度矩阵，再结合FFT技术和谐波合成法模拟得到相应的时间主坐标，最后利用这些时间主坐标与对应的本征模态组建整个随机场，同时给出了相应的误差控制指标.前k阶本征模态的累计能量贡献可由下式估计

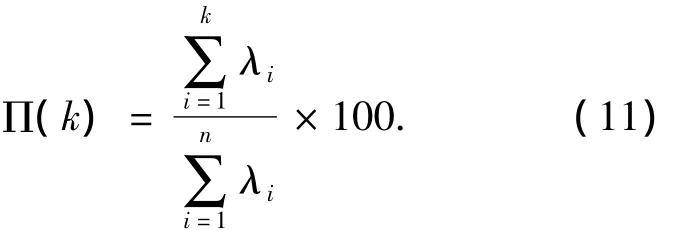
该式可用于选择近似模拟随机场所需的本征模态阶数.例如，要想保证模拟结果具有原有随机过程90%以上的能量，只需通过Π(kλ)≥90来确定kλ的具体取值.

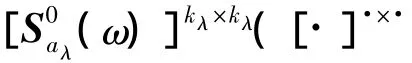
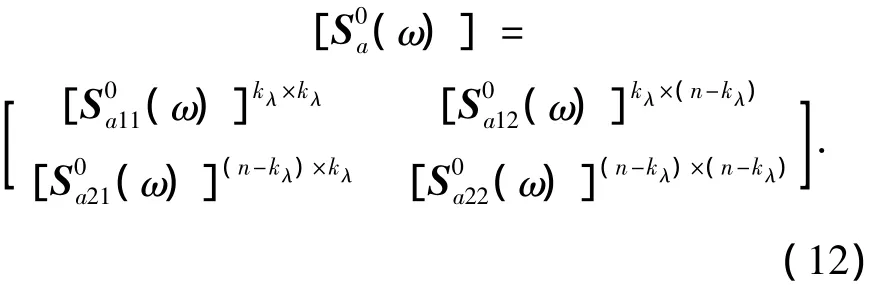
同理随机过程的互谱密度矩阵［S0(ω)］和本征模态矩阵［Φ］也可表示成分块形式，则式(10)表示为

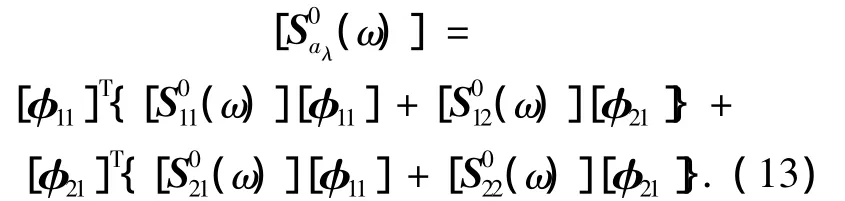
基于前kλ个时间主坐标的互谱密度矩阵采用FFT技术和谐波合成法模拟得到［aλ(t)］，再与相应的本征模态相组合来近似重构随机场:

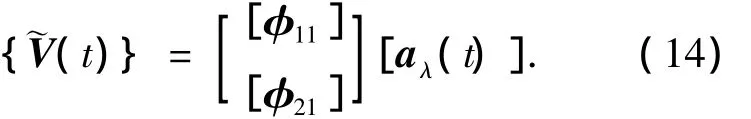
在这里值得注意的是:要想利用式(14)重构得到正确的随机场，由上述方法得到的时间主坐标时程应具有POD分解得到的时间主坐标的正交性质，即an(t)的均方值应等于本征值λn，将在下节算例中验证该特性.

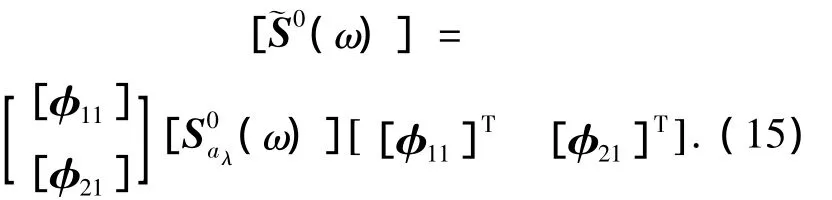
2.3 误差控制

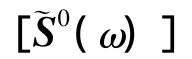
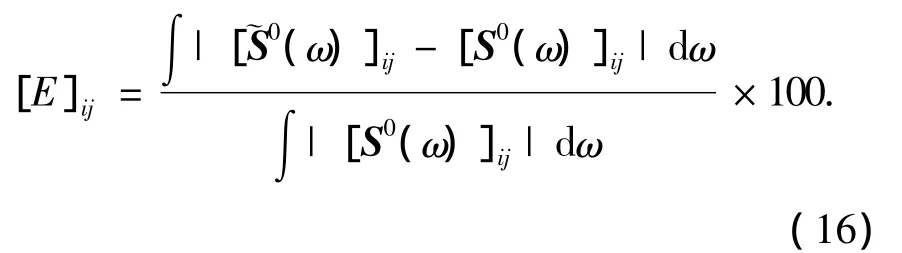
式中［·］ij表示第i行第j列的元素，其最小值、平均值和最大值分别定义最小误差(Emin)、平均误差(Emean)和最大误差(Emax).

在通过式(11)选择模拟随机场所需的本征模态阶数kλ时，可建立一个简单的误差评价指标

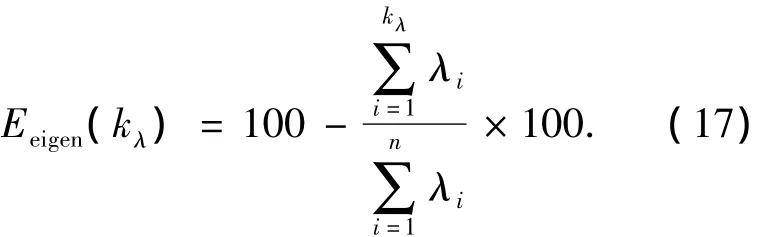
实际应用时可先通过式(17)来选择kλ，然后再检查其他各项误差.

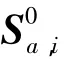
3 数值算例

为了检验上述风场模拟方法的准确性和高效性，选取了空间200个节点来模拟其脉动风速，沿宽度方向(x)的节点间距为6 m，共5列，沿高度方向(z)的节点间距为3 m，共40行.

模拟B类地貌，10 m高处的基本风速为20 m/s，目标谱为 Karman 谱［15］

空间相干函数为

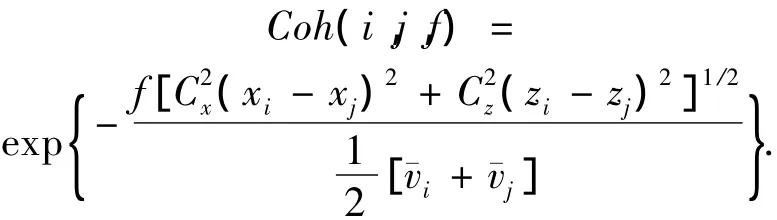
式中取Cx=16，Cz=10.计算时间步长为0.1 s，总时长409.6 s.

图1给出了基于时间主坐标的谱密度矩阵采用谐波合成法得到的时间主坐标的均方值与相应的本征模态之间的比值分布图.所有模态对应的比值都非常接近1，这表明模拟所得到的时间主坐标时程具有POD分解得到的时间主坐标的正交性质，即an(t)的均方值等于本征值λn，也就是说可以采用模拟所得的时间主坐标时程与相应的本征模态相组合来近似重构随机场.

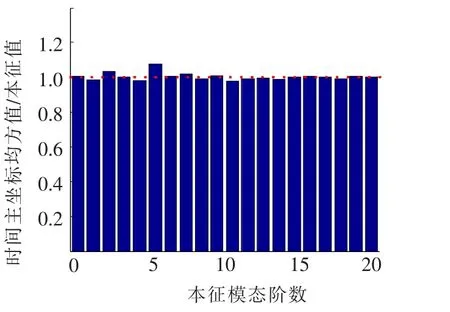
图1 模拟所得时间主坐标与相应本征值的比值分布

图2给出了计算误差随选取的本征模态阶数kλ的变化曲线.随着kλ的增加，数值模拟的计算误差呈现指数形式的衰减趋势，尤其是在前40阶本征模态以前的衰减率很大.当kλ=20，平均误差就可以控制在5%以内，而最大误差也仅15%，也即只要选取前20阶本征模态就可以保证数值模拟精度.图3给出了计算耗时随选取本征模态阶数kλ的变化曲线，所有的计算都是在CPU为P8400＆2.26 GHz，内存为2G的PC机上进行的，编程软件为Matlab.选取前20阶本征模态进行数值模拟时计算所花时间是509 s，而直接用谐波合成法的计算耗时是11 560 s，在本算例中采用结合POD技术的谐波合成法可以节省约95%计算时间，同时可以节省计算内存消耗约35%.

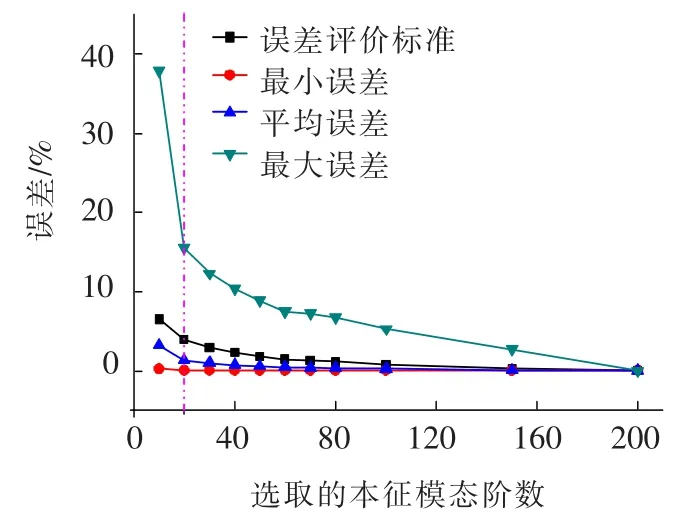
图2 模拟误差随本征模态数的变化曲线

图3 计算耗时随本征模态数的变化曲线

图4、5分别给出了功率谱和互相关函数的对比曲线，本算例中仅需选取前20阶本征模态就可以很好地模拟实际随机场，无论是功率谱还是互相关函数都与目标值很接近.

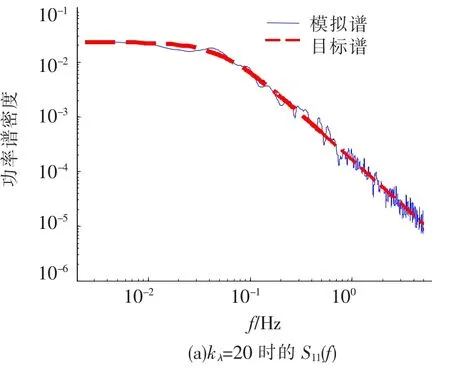
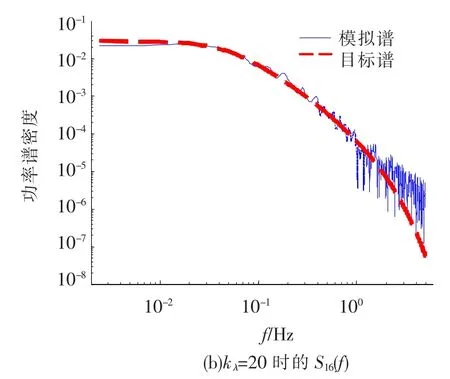
图4 功率谱对比曲线

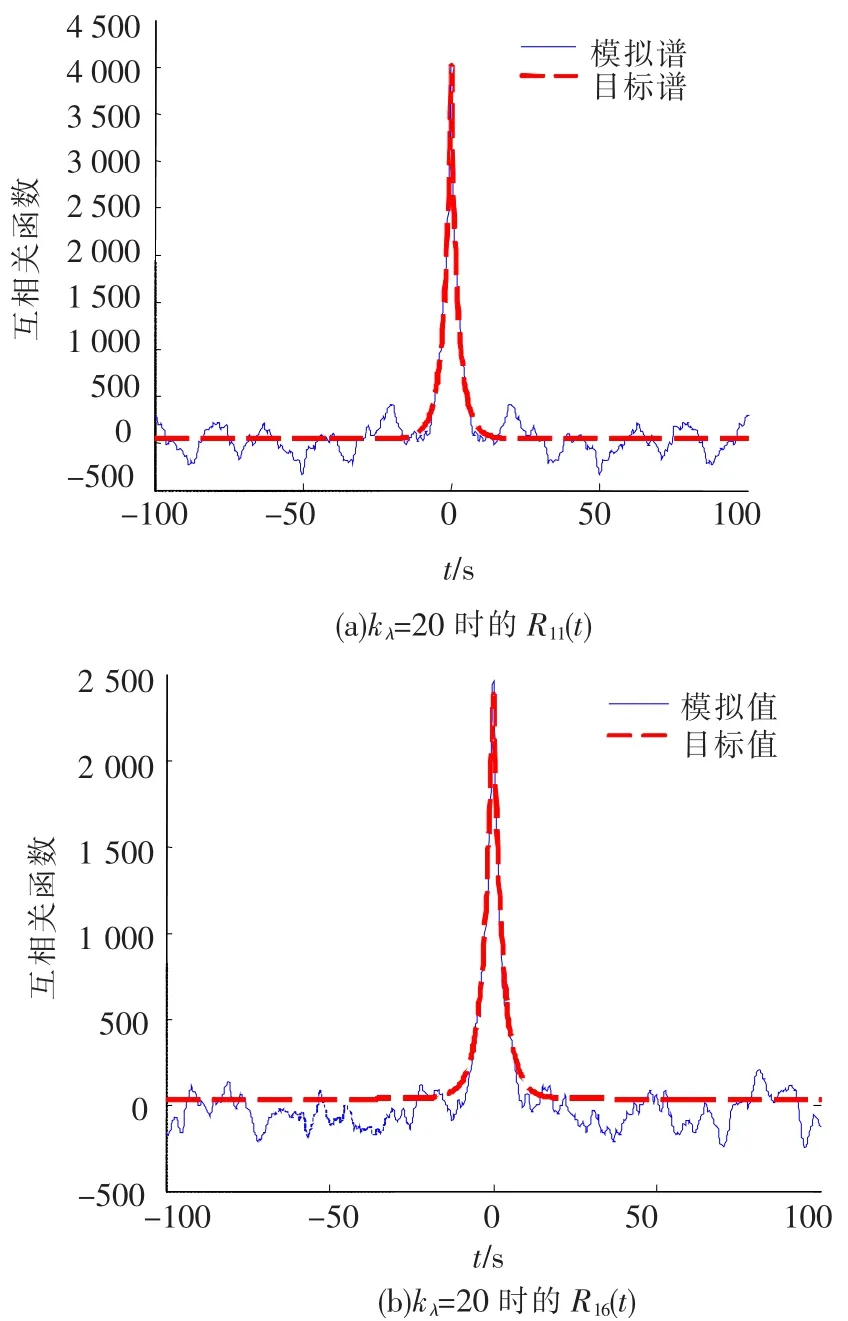
图5 互相关函数对比曲线

4 结 语

采用谐波合成法模拟多节点、多时间步的脉动风场时计算效率低、计算内存超限的问题，从谐波合成法计算效率低下的根本原因出发，引入随机场的高效描述方法——本征正交分解技术(POD)，将其与谐波合成法相结合来模拟脉动风场时间序列，该方法仅需采用谐波合成法模拟少量阶时间主坐标的时间序列就可以近似重构整个随机场，用少量阶数点的互谱密度矩阵Cholesky分解来代替所有点数的互谱密度矩阵Cholesky分解，从而能够大大提高计算效率，降低计算消耗，在随机场的模拟中具有很大的应用价值.

［1］DEODATIS G，SHINOZUKA M.Autoregressive model for non-stationary stochastic processes［J］.J Eng Mech，1988，114(11):1995－2012.

［2］GERSCH W，YONEMOTO J.Synthesis of multi-variate random vibration systems［J］.J Sound Vib，1977，52(4):553－565.

［3］KOZIN F.Auto-regressive moving-average models of earthquake records［J］.Probab Eng Mech，1988，3(2):59－63.

［4］ROSSI R，LAZZARI M.Wind field simulation for structural engineering purposes［J］.Int J Numer Meth Eng，2004，61:738－763.

［5］KITAGAWA T，NOMURA T A.Wavelet-based method to generate artificial wind fluctuation data［J］.J Wind Eng Ind Aerodyn，2002，90:943 －964.

［6］YAMADA M，OHKITANI K.Ortho-normal wavelet analysis of turbulence［J］.Fluid Dyn Res，1991，8:101－115.

［7］SHINOZUKA M，JAN C M.Digital simulation of random processes and its applications［J］.J Sound Vib，1972，25(1):111－128.

［8］YANG J N.On the normality and accuracy of simulated random processes［J］.J Sound Vib，1973，26(3):417－428.

［9］GEORGE D.Simulation of ergodic multivariate stochastic processed［J］.J Eng Mech，1996，122(8):778－787.

［10］曹映泓，项海帆，周颖.大跨度桥梁随机风场的模拟［J］.土木工程学报，1998，31(3):72－79.

［11］罗俊杰，韩大建.谐波合成法模拟随机风场的优化算法［J］.华南理工大学学报，2007，35(7):105－109.

［12］TAMURA Y，SUGANUMA S，KIKUCHI H，et al.Proper orthogonal decomposition of random wind pressure field ［J］.Journal of Fluids and Structures，1999，13:1069－1095.

［13］CHEN X，KAREEM A.POD-based modeling，analysis，and simulation of dynamic wind load effects on structures［J］.J Eng Mech，2005，131(4):325 －339.

［14］HOLMES P，LUMLEY J，BEKOOZ G.Turbulence，coherent structures，dynamical systems and symmetry［M］.Cambridge:Cambridge University Press，1996.

［15］SOLARI G，PICCARDO G.Probabilistic 3－D turbulence modeling for gust buffeting of structures.Probabilistic Engineering Mechanics，2001，16:73 －86.

WAWS/POD simulation of fluctuating wind field

SUN Ying1，LIN Bin2，WU Yue1，SUN Xiao-ying1

(1.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，sunnyhit@hit.edu.cn;2.Beijing Construction Procuring＆ Contracting Trade Center，100083 Beijing，China)

WAWS is the most common used method，and it can produce random data time series with good accuracy，but the low efficiency and memory exceed problem is inevitable at the case of large amout of variates and long time series.An improved method combining WAWS and proper orthogonal decomposition(POD)technique is used in this paper to improve the computational efficiency，which is obviously efficient in both time and memory consumption.Furthermore，an error standard is defined to estimate the simulation precision，which can be used for choosing the order of POD method and error prediction prior to the simulation process.Finally，an example for numerical simulation of 200 points in random wind field is given to demonstrate the accuracy and effectiveness of this method.

fluctuating wind velocity;numerical simulation;proper orthogonal decomposition;weighted amplitude wave superposition

TU393.3

A

0367－6234(2011)12－0013－05

2010－09－06.

国家自然科学基金资助项目(90815021，50908068);哈尔滨工业大学科研创新基金 (HIT.NSRIF.2009098);黑龙江省留学归国科学基金(LC201011).

孙 瑛(1976—)，女，副教授;

武 岳(1972—)，男，教授，博士生导师.

(编辑 赵丽莹)