一种新的Rossler混沌序列图像加密算法

邓 玥，王光义，袁 方

(杭州电子科技大学电子信息学院，浙江杭州310018)

0 引 言

好的加密系统应具有对初始条件的敏感性，以及能将明文充分置乱并改变其统计特性，这与混沌的本质特性对初始条件和参数的敏感性相一致［1］。因而，利用混沌特性加密成为了当今国内外研究热点。近年来，人们尝试用各种混沌序列加密图像和其他信息，但简单的加密序列其安全性不高。本文提出了一种新的图像加密算法，该算法利用混沌序列和乱序映射对象素值进行异或加密和象素位置置乱加密［2］。相比传统的图像加密算法，该算法实现了二次象素加密，一次密钥映射加密，提高了图像保密的安全性。

1 新的混沌系统设计

为了获得一种新的复杂序列，基于Rosslor系统［3－5］，通过引入一个反馈控制，构造了一个新的Rosslor混沌系统:

在这个系统中，状态变量分别为x，y，z，u。其中a，b，c为常量，d为待定常数。可得系统的平衡点:

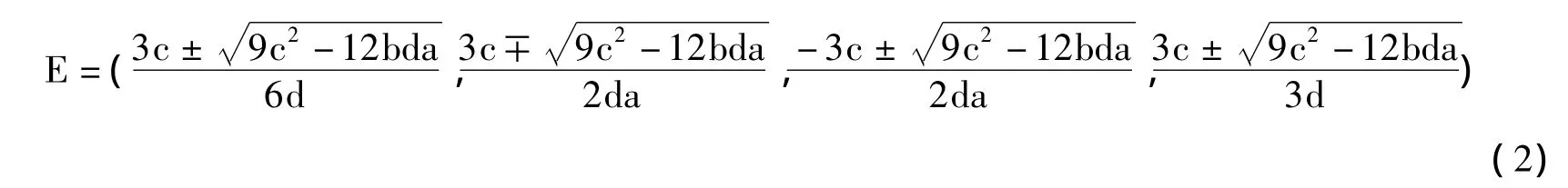
若要使系统产生混沌，必须至少有一个平衡点是不稳定的，即至少有一个特征值(或特征值的实部)是正数。当设置参数值分别为a=0.2，b=5，c=5，d=1时，通过计算可得出系统的特征值分别为:λ1=0.053 4+3.045i，λ2=0.053 4 －3.045i，λ3= －1.832 7，λ4=1.832 7 和 λ1=0.360 1+1.342 7i，λ2=0.360 1 －1.342 7i，λ3= －4.913 6，λ4=1.536 2。存在至少一个特征值(或特征值的实部)是正数，所以此时平衡点是不稳定的，可以满足出现混沌系统的必要条件。

在式1中，令a=0.2，b=5，c=5，d=1时系统是混沌的，通过 MATLAB仿真计算得到的 Lyapunov［5］指数谱图如图1所示，该系统有一个正的Lyapunov指数，这也说明式1是混沌的。因此可利用该混沌系统产生图像加密的流密码。

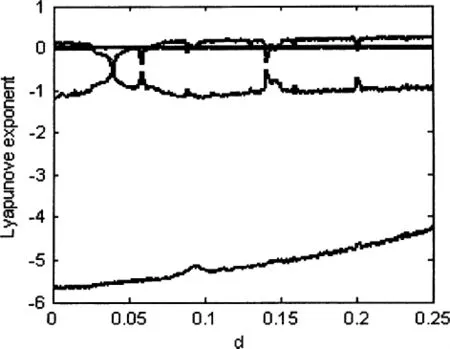
图1 Lyapunov指数谱图

2 图像加密算法设计

传统的图像加密算法有很多，但与混沌加密算法相比，安全性不高，不适合大数据量、实时性要求较高的加密场合。本文采用Rossler混沌系统结合置乱算法，大大扩展了密钥空间，空间复杂度高，具有较高的安全性，避免了单混沌系统加密的信息泄漏问题。其中加密算法设计的流程图如图2所示。

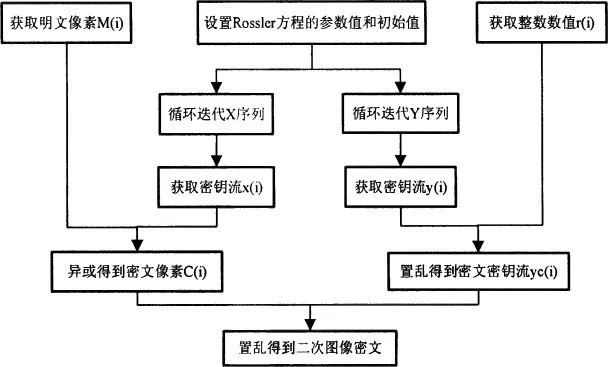
图2 加密算法流程图

该加密算法经过了象素值异或运算和象素位置置乱运算两次加密过程，其中密钥流也是经过置乱加密的，具有较高的复杂度性。加密算法的解密过程与加密过程是逆对称的。解密时，只需要设置相同的初始值和参数就可以实现同步，然后采用置乱运算解密出相应的密文象素值，最后通过逆异或运算可以解密出相应的原始明文象素。加密算法设计中的两个关键技术问题分析如下。

(1)获取加密序列

此次加密序列采用改进Rossler混沌方程的X、Y序列作为流密码，一个对象素值异或加密，另一个对密钥流进行置乱加密。假设图像大小为m×n，首先设置初始值和控制参数，将Rossler混沌方程进行m×n次迭代得到序列X和Y，然而该混沌方程产生的序列并不能直接满足算法的流密码，所以要对序列进行以下变换。

由于象素值大小I∈［0，255］，故X流密码数值大小也要在0－255之间，则有:

式中，Xmax是序列X的最大值，f()表示取整，abs()表示求绝对值。新生成的序列

x(i)即为异或密钥流。由于象素长度为m×n，故Y流密码的大小必须小于m×n。则有:

式中，Ymax是序列Y的最大值。新生成的序列y(i)即为置乱密钥流。

(2)象素加密过程

该算法对象素进行了两次加密运算:其一是象素值异或运算，再是象素位置置乱运算。

异或运算是将象素值M(i)与异或密钥流x(i)进行异或运算得到密文象素值C(i)，过程比较简单，解密时仅再次异或即可恢复到明文象素值。每个象素值对应唯一的象素位置，将象素位置互相打乱亦可达到加密的目的。象素位置置乱的加密过程如下:

1)获取置乱密钥流y(i)和自然数组r(i);

2)把y(i)的第一个数赋给变量T，然后将r(i)的第一个数值和第T个数值进行交换;

3)把y(i)的第二个数赋给变量T，然后将r(i)的第二个数值和第T个数值进行交换，依次向后交换r(i)的每个数值直至全部交换为止，得到密文密钥流yc(i);

4)获取密文象素值C(i)和置乱密钥流yc(i)，并按照步骤(2)、(3)将密文象素值C(i)进行交换置乱得到最终的图像二次加密密文。

置乱的解密过程实际上就是加密的逆过程。把yc(i)的最后一个数赋给T，再将C(i)的最后一个数值和第T个数值进行交换，依次向前交换C(i)的每个数值直至全部交换为止。

3 实验结果

利用MATLAB 7.0为平台，图像大小为256×256，灰度级L=256的Einstein图像进行实验，设置Rosslor混沌方程的初始值均为0.01。图像加密解密的仿真结果如图3所示:

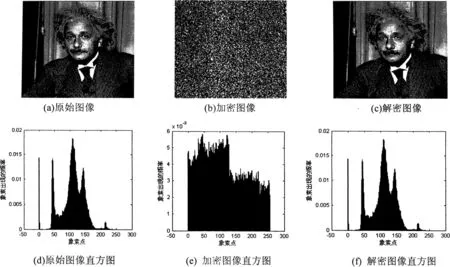
图3 图像的加密、解密过程显示

从实验结果分析:图像加密效果较好，密文图像的直方图分布比较均匀，极大的破坏了明文图像的质量，大大降低了明文象素值之间的相关性，能够良好的抵抗统计分析。同时解密后的图像与明文图像基本没有任何差别，由此可知图像的加解密效果良好。

4 安全性能分析

通过NIST测试［5，6］得知，用以加密的序列具有较好的随机性。以四维Rossler方程的初值作为密钥，因此密钥空间非常大。其次，该算法由二次加密和一次序列置乱构成，复杂度高，同时密钥流进过加密，这样混沌密钥流算法的安全性能比较高，可以有效避免穷举攻击。

5 结束语

本文提出了一个新的图像加密算法，该算法利用改进后Rossler方程所产生的混沌密钥序列与置乱映射相结合，具有较高的复杂性。算法对象素值进行二次加密，且部分密钥也经过加密，有效的抵御统计分析攻击，克服了单一的混沌加密所带来的安全隐患，改善了混沌系统在通信应用中的安全性能。

［1］ Shannon C E.Communication theory of secrecy system［J］.Bell System Technical，1949，28(4):656－715.

［2］ 赵学峰.基于混沌映射的数字图像置乱方法［J］.微电子学与计算机，2003，20(8):136－138.

［3］ Rossler O E.An equation for continuous chaos［J］.Physics Letters A，1976，57(5):397 －398.

［4］ Peng J H，Ding E J，Yang W.Synchronizing hyperchaos with a scalar transmitted signal［J］.Phys Rev Lett，1966，76(6):904－907.

［5］ Wang G Y，Liu J B，Zheng X.Analysis and implementation of a newhyperchaotic system［J］.Chinese Physics，2007，16(8):2 278－2 284.

［6］ Jiang Zhong-Ping.A note on chaotic secure communication systems［J］.IEEE Trans Circ Sys，2002，49(1):92 －96.