不同水位条件下土的自重应力计算

王力威

（常州大学 环境与安全工程学院，江苏 常州 213164）



不同水位条件下土的自重应力计算

王力威

（常州大学 环境与安全工程学院，江苏 常州 213164）

通过理论分析与实例详解指出了严格按照自重应力的定义计算自重应力的合理性，提出了地下水位以下把水的浮力作为外力，在土中产生的是附加应力的观点，进而给出了几种典型水位条件下自重应力及浮力产生附加应力的计算方法，解决了水位以下用浮重度计算自重应力时带来的矛盾等问题，使自重应力的计算简单、容易理解。

自重应力；附加应力；地下水；浮力；渗透力

土的自重应力计算是岩土工程勘察、设计等方面经常涉及的基本工作。自重应力的计算结果影响到建筑地基的变形和地基承载力等相关方面的分析与计算。因此，准确、合理地进行土的自重应力计算非常必要。水平自重应力可由竖向自重应力按侧向土压力系数推得，以下自重应力指竖向自重应力。

1 目前自重应力计算方法与存在问题

计算地表以下土的自重应力时，认为天然地面以下土体为半无限空间体，地面是半无限空间体的表面。

1.1 计算方法

目前通常的自重应力计算方法在地下水位以上均相同，区别在于地下水位以下的自重应力计算，计算方法主要有2种。

第1种方法［1］：地下水位以下均采用浮重度来计算自重应力，即按式（1）计算。

式中 γi为第i层土的重度， 地下水位以下采用浮重度 γ′；hi为第i层土的厚度。

第2种方法：计算的基本公式仍形如公式（1），区别在于地下水位以下要视土的性质来决定是否采用浮重度来计算。砂性土考虑浮力作用，粘性土则视其物理状态而定［2］。

另外，还有认为自重应力是总应力，在地下水位以下用饱和重度计算；把自重应力分为总自重应力和有效自重应力2部分来计算［3］。

1.2 存在问题

1.2.1 计算方法不一致使计算结果差异明显

计算方法不一致，计算结果也相差很大，影响了地基变形和地基承载力等相关方面的分析与计算，造成评价结果不一致，对建筑工程的安全性产生影响。

1.2.2 对地下水存在状态考虑不全面

按目前土的自重应力计算方法，地下水对自重应力计算有影响,但没有说明是潜水还是承压水，实际上，潜水和承压水对自重应力的影响是不同的。而目前所谓考虑地下水应该是考虑的潜水对自重应力计算的影响，而未论及承压水情况下的自重应力计算问题，然而工程实践中,潜水和承压水是都很有可能存在的现象。

1.2.3 用浮重度计算自重应力存在矛盾

自重应力的概念定义为：土受到自身重力作用产生的应力［2］。传统上计算有地下水的自重应力时，认为水的浮力使土的重力减小，即认为考虑地下水时，“土的重量反而减轻了，这就是为什么地下水水位以下采用浮重度计算自重应力的原理”［4］。基于此，在地下水存在并考虑浮力作用时计算自重应力采用的浮重度，实际上是计入了一种外力——浮力，而且浮重度没有计入土中水重，缺失了土中的一相。这样计算得到的“自重应力”，即所谓的“有效自重应力”，已经不是自重产生的应力，实为土的固体颗粒重力与浮力之差产生的应力，偏离了自重应力的原意，也与自重应力的定义相矛盾。而且，地下水位以上计算自重应力的重度计入了土中三相全部重量，地下水位上下采用不同定义的重度来计算自重应力，有不严密之嫌。

2 推荐的自重应力计算方法

自重应力计算，应严格按照自重应力的定义进行，即水位以上仍用天然重度计算，水位以下则采用饱和重度计算。水位以下要把水的浮力，如同渗透力一样，归入土自重以外的力，在土中产生的是附加应力。附加应力与自重应力之和构成土的总应力。具体计算时可视地下水类型，潜水还是承压水，根据水位条件进行具体分析计算。

2.1 潜水情况下的自重应力计算

以下通过实例对潜水情况下的自重应力计算方法加以说明。【例1】 如图1，某地基为成层土，第1层，粘土，γ1=18kN/m3，厚2m；第2层，砂土，γ2=19kN/m3，厚2m；第3层；砂土（地下水位以下），γ3=20kN/m3，厚3m。 计算并绘出沿深度的竖向自重应力σCZ分布图。

【解】 图1中，A、B、C各点自重应力：

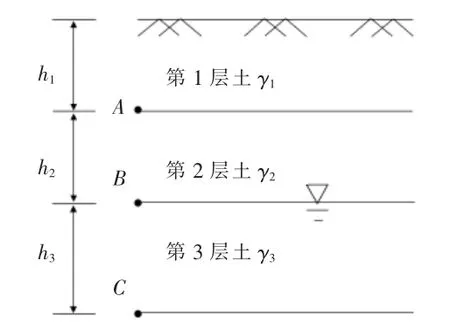
图1 地基中的成层土

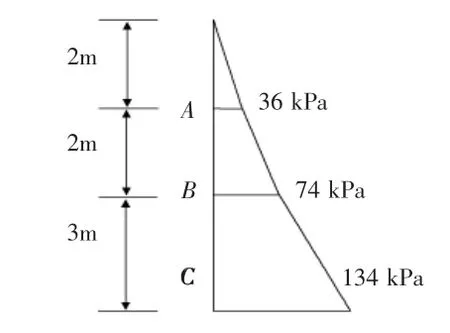
图2 自重应力分布图

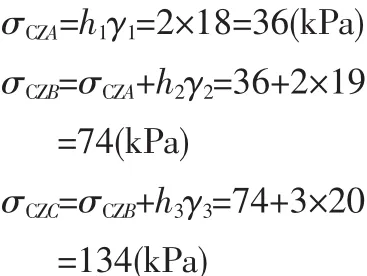
2.2 存在地表水情况下土的自重应力计算

地表水存在情况下，地表面以上的水层可看作竖向均布荷载，是土的外力。此时如地下水位上升至地表，则成为潜水情况的特例。

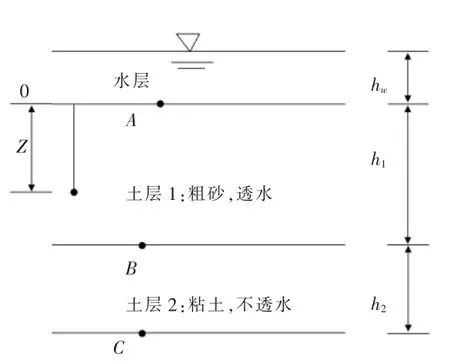
图3 土层情况

【例2】 如图3， 有2层土，上层为厚h1=10m透水粗砂，重度γ1=19.5kN/m3，含水量w=30%；下层为厚h2=5m不透水粘土层，重度γ2=19.3kN/m3；土层上有积水层，层厚hw=3m。取水的重度γ=9.8kN/m3，求水下土的自重应力和附加应力。

【解】 （1）自重应力的计算

地表面A点自重应力σCZ=0

土层1和土层2的交界面B点：σCZB=γ1h1=19.5×10=195(kPa)

C点：σCZC=γ1h1+γ2h2=19.5×10+19.3×5=291.5（kPa）

自重应力的分布如图5（a）所示。

（2）附加应力的计算

土层上面的水层应按外力考虑，在土中产生各点相同的附加应力，其值与深度无关，大小都为σZW1=γwhw=9.8×3=29.4kPa。

至于土层1、土层2中的水，一方面作为饱和土中的一相，与固相土颗粒一同在土中产生自重应力，这在前面已经进行了计算；另一方面在粗砂层，土中水对土颗粒具有浮力作用，可推得单位体积土体的浮力f（方向向上取负号）计算式为：

式中 w为土的含水量。

本例中浮力(体力)

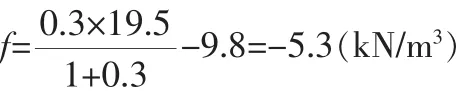
则该力在深度z的土中产生的附加应力（设正号表示由向下的力产生，负号由向上的力产生）为：

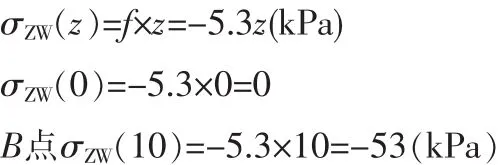
A点附加应力之和

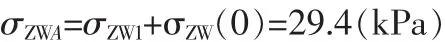
B点附加应力之和σZWB=σZW1+σZW（10）=29.4－53=－23.6(kPa)

不透水粘土层中附加应力仅由土层以上水层产生，各点均为σZW1=29.4（kPa），如图4（a）。

总的附加应力为土层上水层与土层中的水产生的附加应力的叠加，如图4所示。

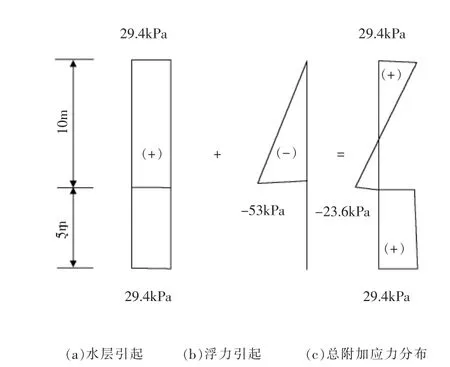
图4 附加应力的计算

总应力为自重应力和附加应力叠加，如图5。

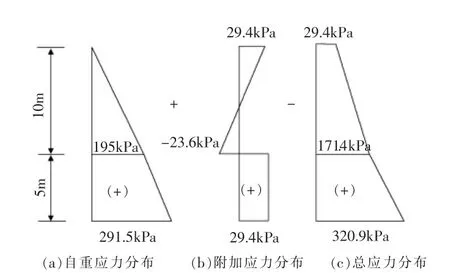
图5 土层中的应力分布

（3）计算方法比较

如采用目前教材中常用算法计算自重应力，则有如图6所示自重应力分布，是B点有突变的折线，这是没有把土中水重考虑进去的结果。

此算法是不全面的，也与自重应力定义不一致。

与图5（a）比较，可见两种算法的区别发生在土层1。本文方法土层1的自重应力较大，是考虑了全部土重的结果；B点只有1个自重应力值，避免了通常计算时1点出现2个自重应力值不易理解的情况。

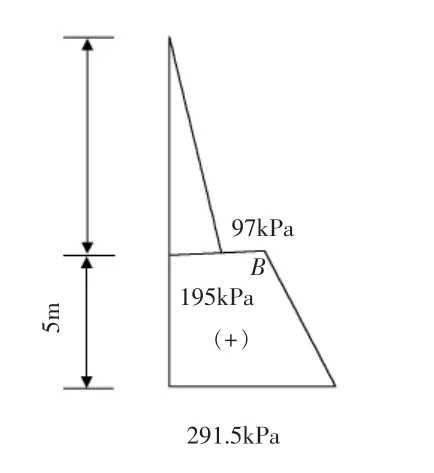
图6 常用算法的自重应力分布

2.3 承压水情况下的自重应力计算

承压水情况下，设土如受到向上的水的渗透力作用，则在土中产生负的附加应力，反之为正。

【例3】 如图7，有自由水面粘土层，在水头Δh作用下，在厚度h2的饱和粘土层内产生稳定渗流,下层为砂层,砂层中有承压水。在粘土层与砂层的界面B处打一侧压管,得知稳定水位高出粘土层面Δh。试求B点Z方向的自重应力、附加应力、总应力，及其分布。已知：水上土重度γ=19kN/m3，饱和重度为γsat=22kN/m3。

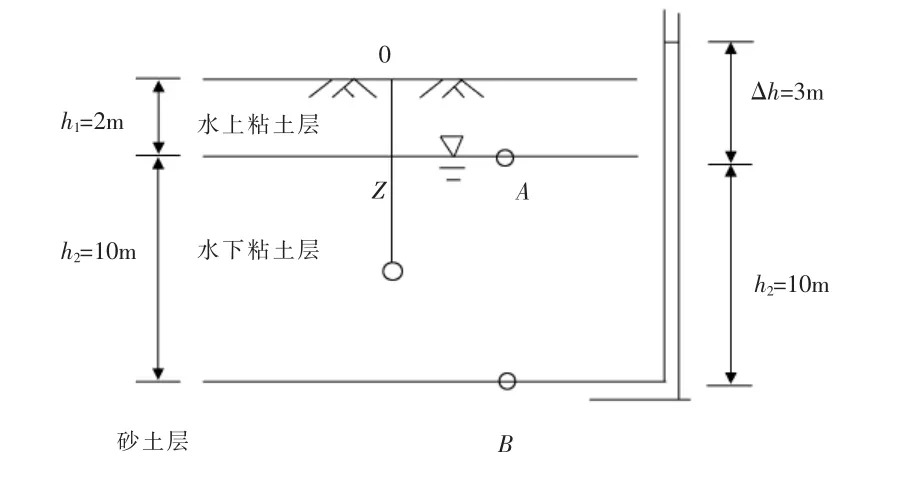
图7 稳定渗流条件下的饱和粘土层示意图

【解】 （1）自重应力计算

如图7，A、B点自重应力分别为：

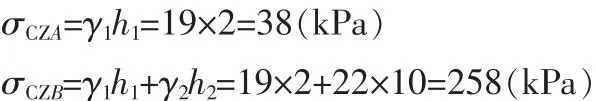
自重应力的分布如图8（a）。

（2）附加应力计算

①当考虑地下水的浮力时

浮力在距地表z处的土中产生附加应力为：

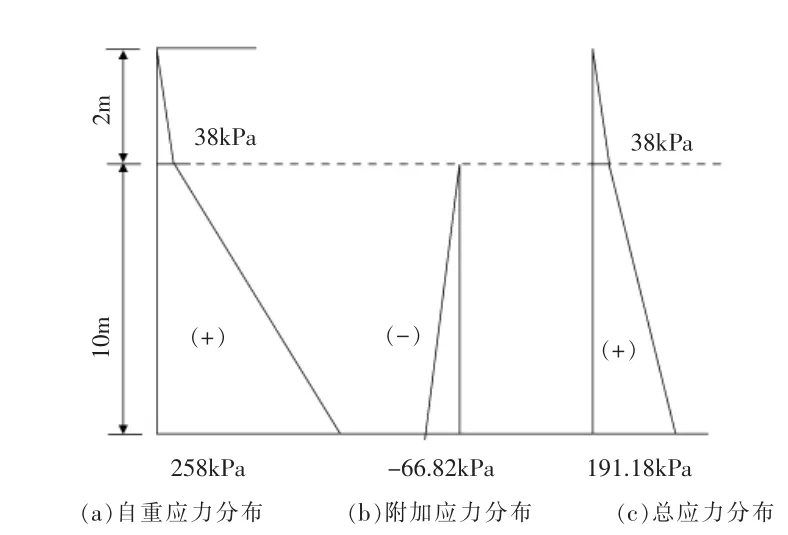
图8 自重应力与附加应力的分布

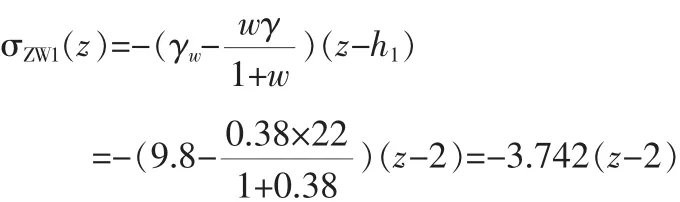
浮力在B点产生的附加应力

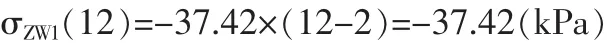
②渗透力的作用

渗透力在距地表z处的土中产生附加应力为

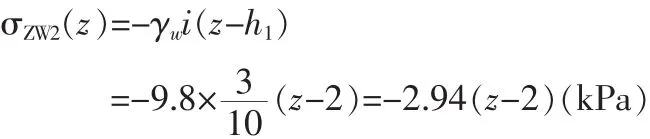
渗透力在B点产生的附加应力

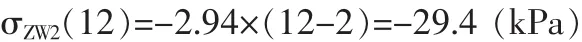
B点附加应力之和σZWB=σZW1（12）+σZW2（12）＝－37.42-29.4=－66.82（kPa）

（3）总应力及其分布图

B点总应力σZB=σCZ+σZWB=191.18（kPa）

附加应力及其与自重应力的叠加情况如图8。

3 结语

水位以下土的自重应力均应严格按其定义计算，而浮力应作为外力来考察，如同渗透力和建筑物、构筑物、人群、车辆、地震等土体以外的作用一样，在土体中产生的是附加应力。据此进行相应的土中应力分析和计算，合适合理、容易理解、计算简单，也避免了有地下水时用浮重度计算自重应力时带来的一些问题，体现了概念应用的准确性。

［1］冯国栋．土力学［M］．北京：水利电力出版社，1986．

［2］袁聚云，钱建国，张宏鸣，等．土质学与土力学［M］．北京：人民交通出版社，2009．

［3］李广信．关于土力学教材讨论的一些体会（一）［J］．岩土工程界，2008，11（9）：21-22．

［4］金日．土体自重应力计算方法的探讨［J］．东北水利水电，2008，26（5）：7．

［5］周东久．关于土体自重应力计算方法及分析［J］．河南交通科技，1999，19（2）：25-26．

［6］赵成刚，白冰，王运霞．土力学原理［M］．北京：清华大学出版社，北京大学出版社，2004．

［7］陈津民．土中的应力——错误的自重应力计算公式［J］．岩土工程界，2003（9）：22-23

Calculation of Soil Self-weight Stress in Different Water Level

WANG Li-wei
（School of Environmental＆Safety of Engineering of Changzhou University，Changzhou213164，China）

Through theoretical analysis and case analysis in detail， rationality of calculation of self-weight stress in strict accordance with the definition of self-weight stress is pointed out，and put forward the viewpoint that take buoyancy of groundwater as external force which produce additional stress in the soil under groundwater level，and then the method of calculating self-weight stress and additional stress produced by self-weight stress and buoyancy under several typical water level is presented，so the problems that contradictions from calculating self-weight stress with buoyancy under water level and so on are solved，and calculation of self-weight stress become simple and easy understood.

self-weight stress;additional stress;groundwater;buoyancy;seepage force

P642.11+6；TU411.3

A

1672-9900（2011）03-0072-03

2011-03-15

王力威（1963—），男（汉族），黑龙江汤原人，高级工程师，主要从事土木工程的教学与研究工作。