连锁故障引发的电网灾难性事故风险评估

何 焱，冯 靖，催 振

(1.西南电力设计院，四川 成都 610021;2.四川大学电气信息学院，四川 成都 610065)

0 引言

灾难性事故评估是电网防灾预灾的重要课题。电网大多能镇定N－1故障，一般不会演化为连锁故障［1］，但由于元件耐受水平不确定［2］，故障物理形式上的潮流转移使数学形式上的风险不断累积，使电网进入临界状态，直至连锁效应阶段［3］，就可能引发灾难性事故，国内外对此开展了大量研究。

文献［4］建立了机组无功出力极限变化与电压崩溃联系模型，I.Dobson 提出了 OPA、CASCAD［5］等模型，但未从整体上揭示规律;文献［6］从结构状态识别脆弱线路;文献［7］将其发展为权重网络;文献［8］发展为有向有权网络，但忽略了运行状态;文献［9］提出状态脆弱性和结构脆弱性概念与评估模型，但对不确定性考虑不足;文献［10］用数学特征评估故障传播。总体上，现有方法考虑了静态影响，对动态影响尚需进一步研究。

元件故障使电网状态偏离，状态漂移累积的潜在风险是其数学表现。电网灾难性事件在时域上是连续的，但可分为累积和连锁两阶段。基于现有研究，这里基于不确定风险理论［11］，结合电网结构状态和运行状态，建立了由静态直接风险和动态潜在风险构成的综合风险指标，揭示出故障风险传播数学规律。以IEEE－9节点系统和某地区电网为研究对象，验证了后提出的方法。

1 连锁故障动态风险评估

灾难性事件过程可分累积效应和连锁效应两阶段［3］。在累积阶段，元件故障带来直接影响的同时，以潮流转移形式在其余元件上累积故障风险。由于电网的镇定作用，在风险累积阶段，传播到下层故障事件的风险小于本层故障事件风险，但一旦漂移到临界状态，若仍存在累积风险，将进入连锁效益阶段，累积风险释放，演变为灾难性事件。因此，分析累积效应和连锁效应至关重要。

1.1 动态潜在风险

单一元件故障能在满足N－1准则的电网中衍变为灾难性事件，是由于关键元件的动态响应造成系统下一时刻的质变引起的。因此，需分析动态潜在风险。

图1 IEEE－14节点系统的左半岛

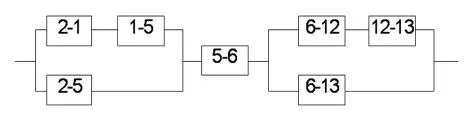
图2 IEEE－14节点系统左半岛的逻辑图

以图1的IEEE－14节点系统左半岛为例，取节点 1、2、5、6、12、13。其逻辑关系如图 2［12］。假设Line1－2故障，与之关联的 Line2－5暴露出极大故障隐患，若Line2－5也故障，平衡节点2必须通过其他路径才能与左半岛联通，这对系统功能实现影响大，会出现状态偏离。虽然节点1和2为发电机节点，没有负荷，两者间线路故障似乎无足轻重，但其关联元件的行为极其关键。故而，对于电网中故障的风险评估，除了评估本身直接静态风险，还必须计及关联元件的潜在风险。

1.2 综合风险评估

学者们已达成共识，对连锁故障影响程度的评估选择“blackout size”(如停电造成的掉负荷数或影响的地域面积)［13］。这里用负荷损失指标作影响程度指标。电网物理结构复杂，拓扑结构决定运行状态，同时受不等式约束，运行状态也会影响结构状态。电网功能实现程度表现为运行状态偏离程度，偏离越远，运行风险就越大，因此，结构状态与运行状态是评估的一对关键因素［14］。

电网满足“N－1”原则，但2003年美加大停电是在“N－4”后引起大停电的，说明经历了累积阶段后风险才释放出来。累积阶段累积的是动态潜在风险。在灾难性事件发展过程，静态直接风险反映故障危害性，动态潜在风险反映潜在风险，可见，动态风险对灾难性事件的发展有主导作用，需综合考虑直接风险和潜在风险。

1.2.1 静态直接风险

以图1为例，当Line1－2退出后，导致状态偏离，系统负荷损失指标为Loss1－2，反映故障自身导致既定功能不能实现而带来的直接风险，可表示为

式中，Cr1－2为 Line1－2故障可信性测度。

除直接风险外，灾难性事件发展是动态的，故障后，由于结构联接牵动的关联元件状态变化产生的潜在风险开始累积，在累积风险中，若又一故障事件出现，立即产生下一层潜在风险继续累积，直到发生连锁故障事件。

1.2.2 动态潜在风险

IEEE－14节点系统中，若 Line1－2故障，造成线路功率越限、节点电压越限，都会对元件映射出一定的故障可能性，这正是故障元件结构联接关系引起的潜在风险。以负荷损失作严重性指标，可得潜在风险测度。

其中，Crn为Line1－2退出后元件映射出的故障可信性测度;Lossn为负荷损失指标。

1.2.3 综合风险

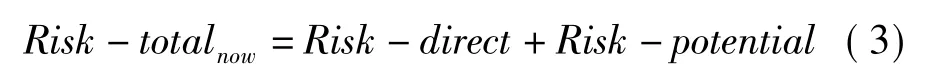
故障直接风险和潜在风险是其危害性的两方面，忽略任一方面都不能作出清晰解释。综合考虑电网灾难事故的动态过程，可对电网灾难性事故作出预测，可采用综合风险测度得式(3)中，Risk－direct为直接风险，Risk－potential为潜在风险。以按综合风险对连锁故障序列排序，可更好刻画故障序列在灾难性事件过程中的风险。

1.3 累积效应和连锁效应阶段

元件故障退出后的风险会牵动下一层故障发生，如式(4)。如果风险传递关系呈递减趋势，电网能镇定风险;若呈递增趋势，当运行于临界状态时，将引起连锁故障事件。

电网对故障有一定镇定作用，一定程度的故障不会自持地传播，电网处于累积效应阶段，其数学特征为故障引发的风险小于触发下层故障事件而带来的风险。但随着事件发展，当漂移到临界状态时，电网会转入连锁效应阶段，已累积风险释放，数学特征为故障事件引发的风险大于触发下层故障事件而带来的风险。

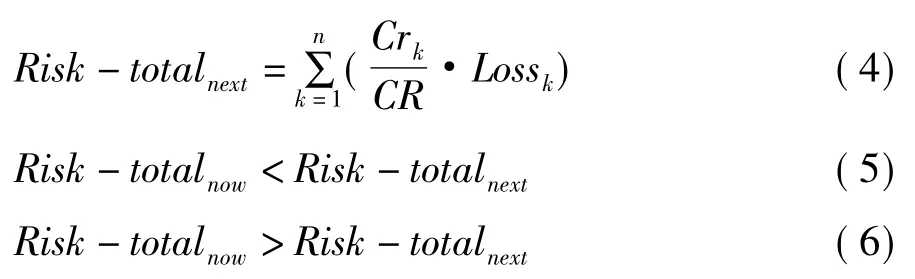
式中，Crk故障为引发下一层元件k故障的可信性测度，CR为故障引发下一层元件故障的可信性测度之和，Risk－totalnow为本层故障的综合风险指标，Risktotalnext为以下层元件故障综合风险指标。

2 灾难性事件评估

2.1 评估模型

为减小灾难性事件风险，需建立以预警决策系统为核心的应急管理平台［15］。通过离线分析建立预警决策性事故序列库，在实际故障时，仅需简单地辨识事故序列。灾难性事件源于N－1事故，初始事件发生后会触发一系列反应，当电网漂移到距稳定状态不远时，处于风险累积效应阶段，该过程缓慢，当风险累积到临界状态时，如果继续累积，风险就会释放出来，进入连锁效应阶段。

以N－1事故作灾难性事件的初始事件，以隐性故障模式刻画故障传播机理。根据本层故障引发的风险与下层故障事件风险相比较，将故障发展过程分为累积效应阶段和连锁效应阶段。在累积效应阶段筛选出最严重的Q组事件作下层仿真的触发事件，当系统潮流不收敛或丢失负荷超过20%时［16］仿真停止。

2.2 评估算法

电网灾难性事件动态综合风险评估流程如下。

1)读取拓扑结构和电气运行的初始参数，进行初始状态的潮流计算，得出元件承受扰动的耐受区间。

2)计算各N－1故障的综合风险指标，并对其降序排序。

3)按排序结果，依次搜索各事件对应的下一层暴露元件，并按其修改结构参数。

4)搜索拓扑结构是否形成孤岛，若“是”，准备进行多区域潮流计算;若“否”，进行故障后潮流计算。由潮流计算结果得出维持故障后拓扑结构的可信性测度，按式(1)得到故障事件的直接风险，按式(2)得到故障事件牵动的潜在风险，最终得出故障事件的综合风险指标式(3)。

5)将本层故障事件的综合风险与上一层故障事件的综合风险相比较，若式(5)成立，按照风险降序的原则，将事件保存到连锁效应阶段;若式(6)成立，按照风险降序的原则，将故障事件保存到累积效应阶段，并从本层累积效应阶段筛选出综合风险最高的前Q组事件。

6)判定系统负荷损失时是否小于20%，若“是”，转入步骤3);若“否”，停止仿真。判定是否到达最大搜索层数，若“是”，则结束仿真;若“否”，则转入步骤3)。

3 仿真

3.1 累积效应阶段风险排序

对IEEE－9节点系统进行仿真，如图3，并与传统方法比较。传统方法将各类严重度指标加权得整体影响严重度，权重系数如表1。用该方法对N－1事故进行分析，结果与传统风险评估法1、2进行比较，如表2。

图3 IEEE－9节点系统

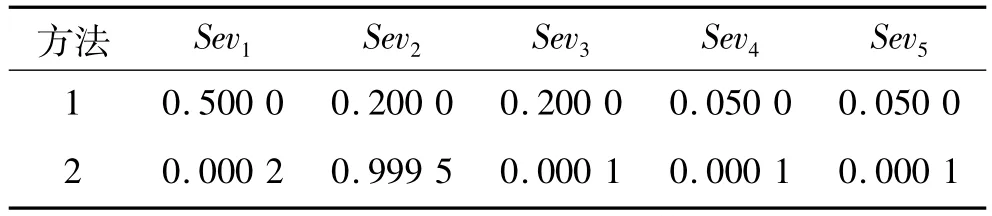
表1 传统风险评估方法权系数

表2 N－1事故排序

可见，本方法与传统方法有较多相似处，特别对于最严重和最不严重N－1故障的认同度高。当L7和L9故障后，导致G1、G2与系统解裂造成严重影响，与工程实际相符。

3.2 连锁效应阶段风险排序

后续连锁故障序列的评估以N－1事故为起始事件，从起始事件中筛选出风险最大的q组事件，送入下一轮连锁事件序列的搜索中，以此类推，直到搜索至最大搜索深度为止。由所提方法得出的后续连锁故障事件如表3。

表3 连锁效应阶段的故障序列排序

3.3 实际电网累积阶段风险排序

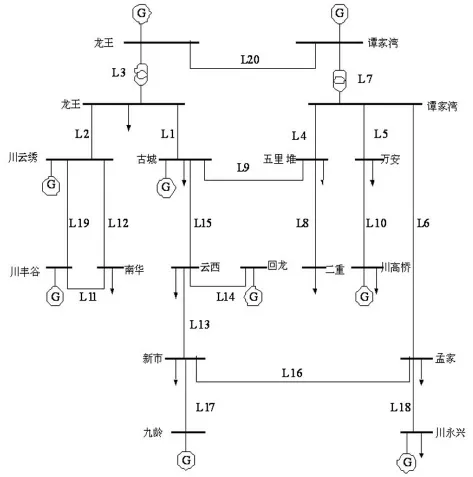
图4 丰水期某地区电网的节点图

以图4实际系统为例，系统处于负荷高峰时刻，能考验该电网接纳负荷的能力，电网输变电设备均投入运行。建模时将电网中500 kV和220 kV站等效为节点，110 kV及以下的变电站等效为对应220 kV节点的负荷。

以N－1事故风险排序作为连锁性事故的起始事故，进行事故风险排序，结果如下。

表4 丰水期N－1事故风险排序

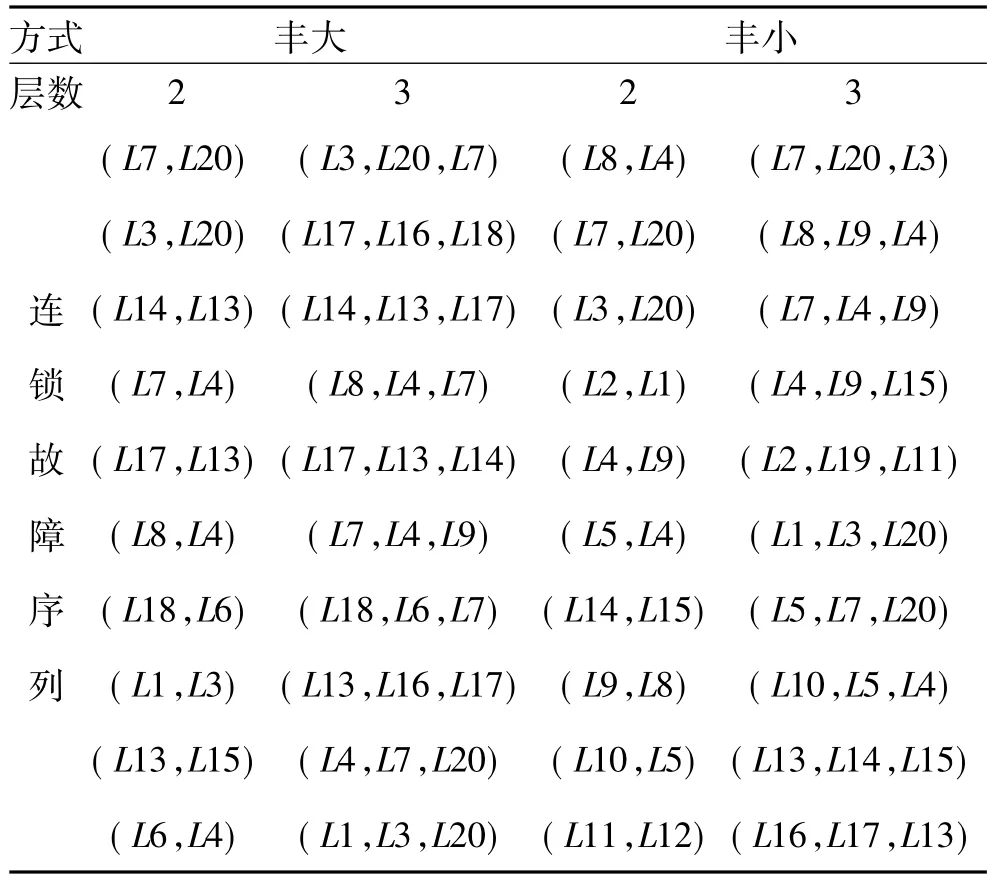
表5 丰水期累积效应阶段事故风险排序

3.4 实际电网连锁阶段风险排序

根据N－1风险排序结果，对系统崩溃序列进行评估，如表6，可见，结果与实际相符。

表6 丰水期的连锁效应阶段故障序列排序

4 结语

虽然电网对N－1故障具有镇定作用，但事故传播具有不确定性。在N－1故障模式下，薄弱环节的隐性故障引发的风险不断累积，电网逐渐偏离稳定状态，但风险累积效应阶段是相对缓慢的，在此阶段可尽力阻止电网进入故障连锁效应阶段。由于基于结构状态和运行状态，评估由静态风险和动态风险组成的综合风险，根据故障传播数学属性提出了一种新的电网灾难性事故评估方法。对理论模型和实际模型的仿真证明，所提方法正确、合理，具有一定的工程应用价值。

［1]于会泉，刘文颖，温志伟，等.基于线路集群的连锁故障概率分析模型［J］.电力系统自动化，2010，34(10):29－33，61.

［2]肖先勇，陈卫东，杨洪耕，等.以用户满意度区间数为测度的电压暂降频次评估［J］.中国电机工程学报，2010，30(16):104－110.

［3]丁道齐.复杂大电网安全性分析—智能电网的概念与实现［M］.北京:中国电力出版社，2010:136－145，221－223，293 －294.

［4]Overbye T J，Demarco C L.Voltage Security Enhancement Using Energy Based Sensitivities［J］.IEEE Trans on Power Systems，1991，6(3):1196 －1202.

［5]Dobson I ，Carreras B A，Lynch V E，et all.Estimating Failure Propagation in Models of Cascading Blackouts［C］.8th International Conference on Probabilistic Methods Applied to Power Systems，Ames，USA，2004:641 －646.

［6]陈晓刚，孙可，曹一家.基于复杂网络理论的大电网结构脆弱性分析［J］.电工技术学报，2007，22(10):138－144.

［7]丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估［J］.中国电机工程学报，2008，28(10):20 －25.

［8]张国华，张建华，杨京燕，等.基于有向权重图和复杂网络理论的大型电力系统脆弱性评估［J］.电力自动化设备，2009，29(4):21 －26.

［9]魏震波，刘俊勇，朱国俊，等.基于电网状态与结构的综合脆弱评估模型［J］.电力系统自动化，2009，33(8):11 －14.

［10]Kim J，Dobson I.Approximating a Loading － Dependent Cascading Failure Model With a Branching Process［J］.IEEE Transactions on Reliability，2010，59(4):691 －699.

［11]Liu Bao － ding，Uncertainty Theory［M］.Beijing:Uncertainty Theory Laboratory，2010，http://orsc.edu.cn/liu.

［12]Daniele Codetta － Raiteri，Andrea Bobbio，Stefania Montani.A dynamic Bayesian Network Based Framework to E-valuate Cascading Effects in a Power Grid［J］.Engineering Application of Artificial Intelligence，In Press，Corrected Proof，2010.

［13]Z.J.Bao，Y.J.Cao，G.Z.Wang ang L.J.Ding.Analysis of Cascading Failure in Electric Grid Based on Power Flow Entropy［M］.Physics Letters A，2009，373(34):3032 －3040.

［14]韩祯祥.电力系统稳定［M］.北京:中国电力出版社，1995:147－151.

［15]田世明，陈希，朱朝阳，等.电力应急管理平台研究［J］.电网技术，2008，32(1):26 －30.

［16]Hazra J，Sinha A K.Identification of Catastrophic Failures in Power System Using Pattern Recognition and Fuzzy Estimation ［J］.IEEE Transactions on Power Systems，2009，24(1):378－387.