基于模糊数学方法的铁路客运站站房结构造价快速估算研究

吴建平，成 泉

（1.铁道部经济规划研究院 工程设计鉴定中心，北京 100038；2.北京交通大学 土木建筑工程学院，北京 100044）

1 概述

目前，我国已经建成了北京南站、广州南站、武汉站、上海虹桥站，以及武广、郑西等高速铁路沿线一批现代化的大中型铁路客运站。在这些铁路客运站的工程投资中，结构工程投资占整个客运站投资的 40%～50%，结构工程费用的快速估测对建设决策十分必要。

模糊数学方法在我国工程造价控制方面有着广泛的应用。王祯显[1-2]首先将模糊数学引入工程投资估算，创造性地利用典型工程建设经验，为工程投资估算提供了有效的方法和途径。王祯显认为这种方法最重要的是计算两个工程的相似性 (贴近度)，只有选择了正确的相似样本，估算的结果才会准确，而相似度的计算是建立在模糊数学方法上的。沈良峰[3]应用模糊数学的理论和计算方法，建立了一种建筑工程造价的快速估算模型。作者构建典型工程的特征值矩阵，通过公式转换，建立典型工程的隶属度矩阵，提出了一种新的确定隶属度的方法。周尚洁等[4]研究了模糊数学方法在水电工程造价估算中的应用。万菁等[5]提出了以模糊数学为理论基础的模糊比较估价法，应用于水电工程的工程造价管理，取得了很好的效果。

由于铁路客运站的复杂性和多样性，到目前为止还没有专门的估测方法对其结构费用进行估算。我国绝大部分施工企业或项目审批单位是基于传统思路计算客运站结构工程的造价，此项工作十分繁琐而复杂，效率不高，不利于审批单位快速对投标进行评估，即使使用计算机编制预算，计算工程量所需的数据仍需人工收集。为此，应用模糊数学分析方法对客运站结构工程造价进行快速估算，以期为客运站的建设提供参考。

2 快速估算方法数学模型

由于铁路客运站工程本身的单体性、复杂性、多样性，以及客运站不同地区、不同自然因素等特点，实际上并不存在两个完全相同的客运站，但是在众多的客运站工程之间存在着某些相似性，只是相似程度不同而已。因此，可以将若干个最相似客运站的造价作为原始资料，在此基础上利用估价模型估算出拟建客运站的造价。以侧式站房为例，运用模糊数学方法对铁路客运站站房结构费用进行快速估算。

2.1 提取模糊综合评价比较层项目

在客运站结构设计和建设过程中，不同的结构体系其工程造价有较大的差异。对于同一结构形式，受到跨度、柱距、层高等因素的影响，其造价也存在较大的差异。因此，需要确定这些影响因素的重要程度并提取对结构工程费用影响较大的因素。

比较层项目是进行工程造价估算时的分项工程，所有的比较、识别和估算都是在比较层项目上完成的。可以采用主成分分析的方法确定铁路客运站侧式站房比较层项目的特征向量集，分析侧式客运站结构体系、自然条件及站房结构参数等影响客运站结构体系造价和工程数量的因素，得到影响客运站造价及工程用量的重要因素，以及各影响因素的重要程度，作为建立特征向量集的基础。

2.2 选取相似客运站

2.2.1 确定隶属度

将各客运站视为评判指标上的模糊集，为了反映评判指标的不同规格 (或型式) 对客运站造价的影响，引入隶属度概念[6]。确定隶属函数值需要通过逐步修正而加以完善，针对已经完成的典型客运站的实际估测是检验和调整隶属函数值的依据[7]。

2.2.2 确定特征向量权重值集合

权重值反映各客运站特征向量对客运站造价的重要程度，有专家评议综合法、二元对比法等确定方法，以下采用二元对比倒数法确定工程特征权重。

（1）建立比较矩阵。对于某一比较层项目，其评判指标集合 T 为：

按各指标对实现目标的影响程度，两两比较各评判指标，赋以确定值，从而得到一个 n 阶对比矩阵 A。

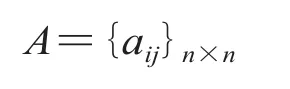
（2）计算权向量。根据得到的比较矩阵，采用优势积累法计算权向量，采用“和”法进行计算。

步骤 1：将矩阵的元素按列进行归一化。

步骤 2：求出矩阵的“行和”，得出“行和”向量矩阵 V。

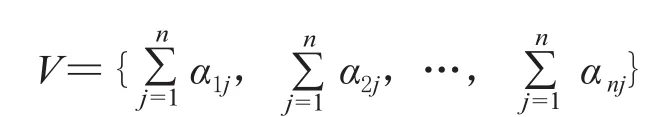
步骤 3：对“行和”向量进行归一化处理，即可得到权重值集合W。

2.2.3 计算贴近度

贴近度是表示两个模糊集接近程度的定量指标。采用加权海明距离贴近度公式，计算拟建比较层项目P与各已建的比较层项目Q的贴近度，即：

式中：Wi为加在µi上的权重，满足归一化条件，即∑Wi＝1。

2.2.4 选择相似客运站

通过测算拟建客运站与已建客运站的贴近度，定量化拟建客运站的相似程度，将计算出的拟建客运站与每一个已建客运站的贴近度进行从大到小排序：σ1，σ2，σ3。按照择近原则，选取前3个加权海明距离近或贴近度大的客运站的站房结构造价。加权海明距离越近或贴近度越大，说明两个模糊子集相似程度越高。

2.3 估算拟建客运站侧式站房造价

得出3个相似度最高的客运站后，从已经收集到的客运站数据中提取出各自对应的站房结构费用E1、E2、E3。应用指数平滑法计算拟建客运站侧式站房的造价Ex，公式如下：

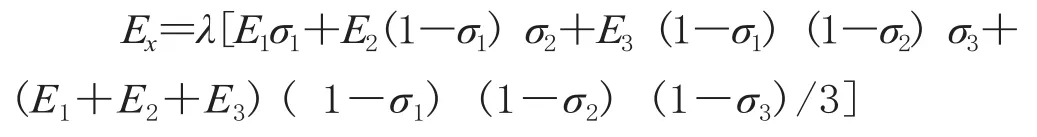
式中：λ为调整系数。其经验公式为：

式中：m为比较层项目的个数 (本文为 10)；Ba为拟建客运站的模糊关系系数，Ba＝(b1＋b2＋…＋b10)/10；Aσ1、Aσ2、Aσ3为已建客运站的模糊关系系数。

将测算的拟建客运站站房结构费用作为已知值，列入数据库的已建工程中，重复计算步骤得出典型客运站的造价，校验计算精度。

3 铁路客运站站房结构造价快速估测流程

通过总结模糊估测流程，铁路客运站站房结构造价快速估测总流程图如图1所示，利用模糊数学方法估算每个比较层项目的核心子流程如图2所示。

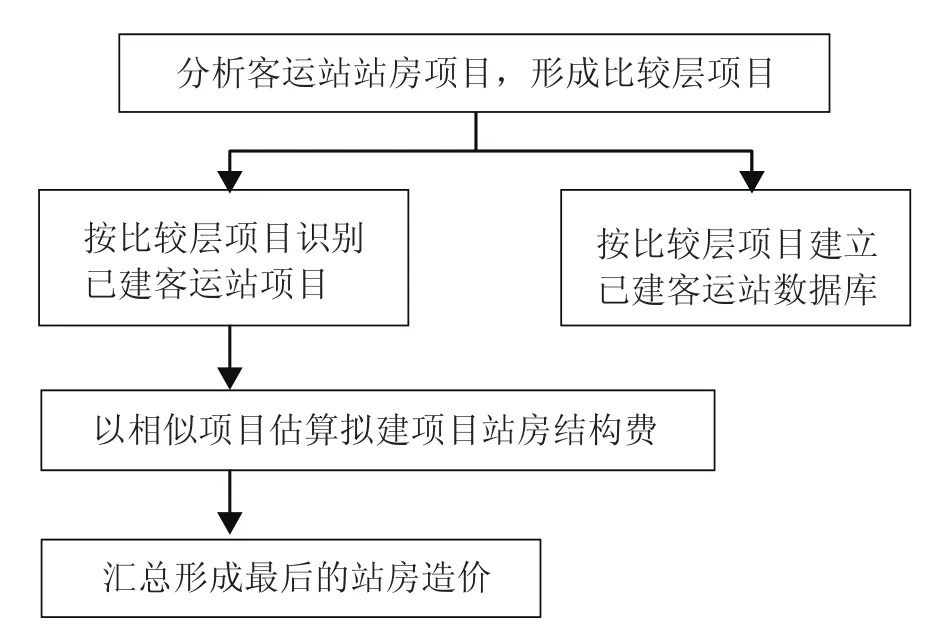
图2 估算每个比较层项目的核心子流程图

4 工程实例分析

4.1 选取特征向量集

经过主成分分析及对实际情况进行综合考虑后，提取对铁路客运站侧式站房结构费用影响最大的特征向量集R。

R＝{站房面积，站房建筑高度，抗震设防烈度，楼盖主要柱网，楼盖柱的结构高度，楼盖结构投影面积，屋盖主要柱网，屋盖柱的高度，混凝土屋盖结构投影面积，钢结构屋盖结构投影面积}

依托收集到的工程数据资料建立 45 个已建并符合要求的客运站工程特征因素和结构费用数据库。为了验证模糊数学方法的准确性，从中选取4个典型站房工程，进行实例测试。根据设计资料，4个客运站站房对应的 10 个比较层项目的工程量数据如表1所示。

4.2 确定特征向量隶属度

确定隶属度需要在 Matlab 中编程计算，采用 S型函数大致确定相应客运站对应的特征因素的初始隶属值。利用初始隶属度和确定的权重值，以及已有的客运站样本进行试算，经过反复调试确定最终的隶属度。为了方便后续新建客运站隶属度的赋值以及程序的编写，尽量使隶属度与各特征因素数值的范围相一致，按一定的区间范围递增。经过反复调试和测算，10 个特征向量的隶属度如表2所示。

表1 4个客运站的比较层项目数据

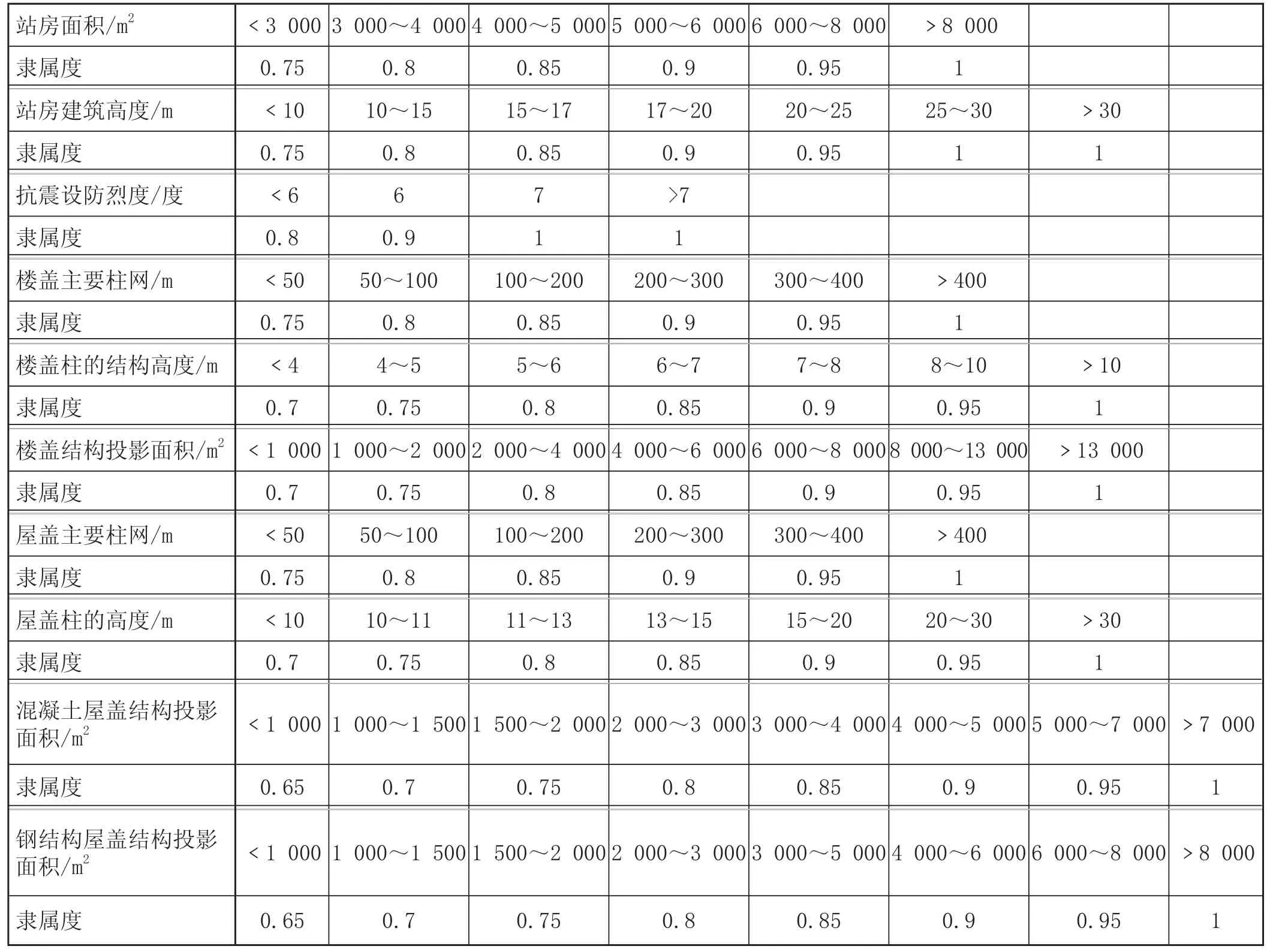
表2 10个特征向量的隶属度

4.3 特征向量权重值的确定

采用二元对比法确定权重值，归纳得出各工程特征因素的权重值向量集W。

W＝{0.2490，0.1670，0.0247，0.0622，0.0622， 0.1670， 0.0366， 0.0622， 0.0622，0.1070}

4.4 算例测试结果

根据造价的估测流程，确定贴近度，4 个拟建客运站站房结构费用的估算值与实际值之间的误差如表3所示。经过多个算例分析，只要建立了足够多数据的数据库，一般计算误差可以控制在 5% 以内，满足工程估价的精度要求。

表3 4个拟建客运站站房结构费用的估算值与实际值之间的误差

5 结束语

应用模糊数学分析方法实现了对客运站结构费用的快速估算，计算结果表明估算精度较高，可以为客运站项目的评估及决策提供参考依据。由于快速估测计算中需要有大量的经验测定，因此只有在应用中积累经验，才能正确有效地确定客运站比较层项目、隶属度值及权重值，从而达到快速、精确的估算目的。

[1] 王祯显. 模糊数学在土建工程中的应用[J]. 土木工程学报，1986(2)：88-92.

[2] 王祯显，廖小建，杜晓玲. 工程造价快速估算新方法及其应用[M]. 北京：中国建筑工业出版社，1998.

[3] 沈良峰. 建筑工程快速估价的一种模型及应用[J]. 工业工程与管理，2004(6)：83-84.

[4] 周尚洁，强茂山，周 伟. 水电工程快速估价系统的研究与开发[J]. 水力发电，1998(11)：1-3.

[5] 万 菁，芦京莲. 水电工程造价的快速动态估算新方法研究[J]. 水电站设计，2000(6)：67-69.

[6] 张 跃，邹寿平，宿 芬. 模糊数学方法及其应用[M]. 北京：煤炭工业出版社，1994.

[7] 张 炜，王亚平，林 杰. 工程合理成本的模糊估测模型及应用研究[J]. 铁道学报，1998(3)：19-21.