基于k短路径算法的多目标最短路径算法
2011-07-11康太平张晓刚王宗峰何尚录
康太平 张晓刚 王宗峰 何尚录
(兰州交通大学数理与软件工程学院,甘肃 兰州 730070)
基于k短路径算法的多目标最短路径算法
康太平 张晓刚 王宗峰 何尚录
(兰州交通大学数理与软件工程学院,甘肃 兰州 730070)
为满意地解决多目标最短路径问题,提出基于循环搜索第k短路径,构造新集合做交集的多项式算法。该算法是在每一轮的k短路搜索完以后,通过交集产生多目标最短路径或备选路径。当有多条备选路径时再用Vague集投影和距离的决策方法,根据评价值的大小对候选方案进行排序,从而选取最佳方案。
多目标;第k短路径;Vague集
0 引言
经典的最短路问题只涉及单目标优化[1],即从起点到终点路程最短或费用最少,但实际问题中,如在铁路旅客运输中,人们总是希望乘坐快速、舒适、便宜的列车去旅行,列车的运行时间、速度、列车级别、票价等构成了多目标路径问题。求解过程中有多个目标需要优化,这就拓展出多目标最短路径问题。由于多目标问题目标间往往存在的不相容性或目标的不可加性,造成了多目标问题的难解性。要使多个目标在一个方案中均达到最优,是很难得到这样的解的,实际上,也很少存在这样的最优解。多目标最短路径问题一般不存在单一的最优解,而只有满意解也称Pareto解[2-3]。目前,应用广泛的有效用函数法、遗传算法、蚁群算法等。通过改进文献[4]中提出的方法,提出了基于k短路算法[5]的多目标最短路径算法,通过逐次找目标的第k短路径,构造新的路径集作交集而得出多目标最短路径。
1 多目标最短路径算法
多目标路径选择问题一般可描述为:对于G=(N,E),节点集为N,节点间的有向边的集合为 E,|N|=n,|E|=m。令 Aq(q=1,2,…,Q)表示第 q 个目标值,Aq(i,j)(q=1,2,…,Q)为从节点i到节点j的第q个目标值,求从起点O到终点D之间的最短路径。
定义2 第 k短路径——若 p1,p2,…,pk为顶点v1至顶点v的k条路径,W(p1)≤W(p2)≤…≤W(pk),现p为顶点v1至顶点v的任一条路径,p∉{p1,…,pk},且 W(p)≥W(pk),则称 pk为顶点v1至顶点v的第k短路径。
2 多目标最短路径算法的具体步骤
步骤1 利用Dijstra搜索最短路径算法获得网络 G=(N,E)中目标 q(q=1,2,…,Q)的最短路径集(q=1,2,…,Q)。
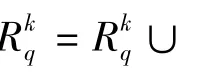
3 算例
图1为从起点S到终点T之间的运输网络图,各条有向边上的目标值见表1。3个成本类目标:目标1为距离,目标2为费用,目标3为事故率,3个目标的权重相等。求从起点S到终点T之间考虑多个目标的最短路径。

图1 S到T的运输网络

表1 各条有向边的目标值



③若备选路径不止1条时,根据文献[6],选用基于Vague集投影和距离的决策方法。发现当所有目标的第5短路径全部搜索完,构造新路径集:


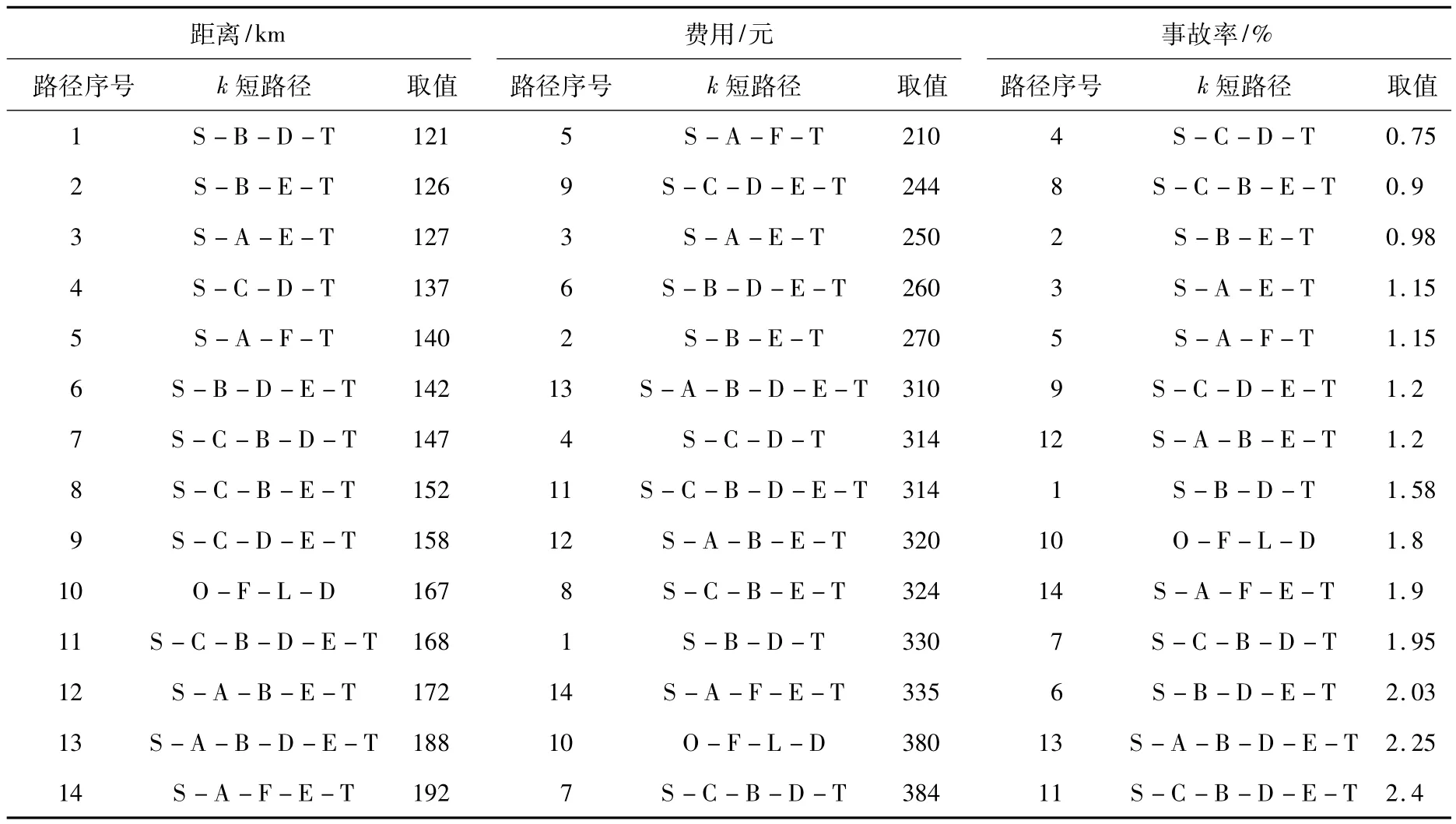
表2 与目标对应的k最短路径及相应的目标取值
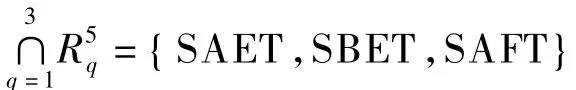
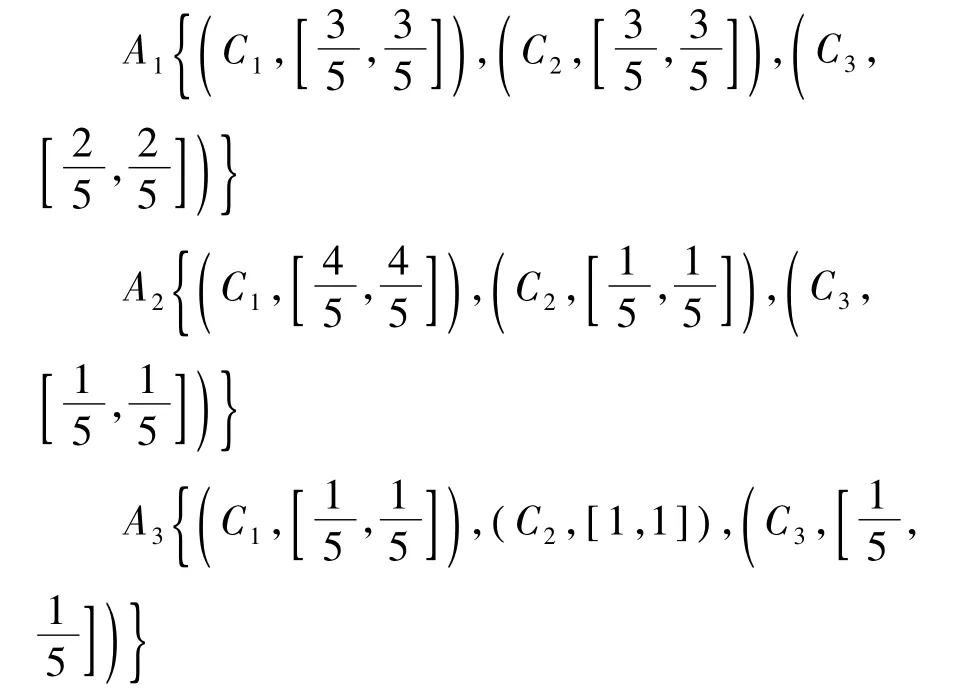
①分别计算各个候选方案的评价值,其中D(Ai,A*)为 Ai方案到理想方案的投影,J(Ai,A*)为Ai方案到理想方案的距离,Z(Ai,A*)为Ai方案的综合评价值,评价值越大则对应的方案越优。

②由 Z(A1,A*) >Z(A3,A*) > Z(A2,A*)得方案的排序为A1>A3>A2,最优方案为A1,方案的排序也符合k短路交集产生的结果。A1为第4短路径搜索完产生的结果,算法结束。为了比较方案的优劣和产生多条备选路径时运用Vague集投影和距离的决策方法,搜索到第5短路径结束时产生了方案A2和A3,运用Vague集投影和距离的决策方法比较得,方案A3比方案A2更优。
4 结论
基于第k短路径问题,给出了多目标最短路径的算法。它是在每一轮的k短路搜索完以后通过交集产生的,当交集为空集时继续搜索下一轮第k短路径再作交集,当交集为一条路径时它就是最先同时满足各目标的最优路径。当交集产生多条备选路径时通过Vague集投影和距离的决策方法比较产生出满足各目标的最优路径,这样每次都是在一轮的k短路搜索完以后才进行交集,也减少了作交集的次数同时提高了计算的效率。
[1]谢金星,刑文训.网络优化[M].北京:清华大学出版社,2000:119-143.
[2]Martins E Q V,Santos J L E.The Labeling Algorithm for the Multiobjective Shortest Path Problem[R].CISUCTechnical Report TR99/005,Coimbra,Portugal:Universityof Coimbra,1999.
[3]Guerriero F,Musmanno R.Label Correcting Methods to Solve Multicriteria Shortest Path Problems[J].Journal of Optimization Theory and Applications,2001(3):589 -613.
[4]郝光,张殿业,冯勋省.多目标最短路径模型及算法[J],西南交通大学学报,2007(5):641-645.
[5]傅家良.运筹学方法与模型[M].上海:复旦大学出版社,2005:238-241.
[6]要瑞璞,沈惠璋.基于Vague集投影及距离的模糊多指标决策[J].数学的实践与认识,2009(2):19-22.
Algorithm for Shortest Path of Multi-objectives Based on k Short Parth Algorithm
KANG Tai-ping ZHANG Xiao-gang WANG Zong-feng HE Shang-lu
(School of Mathematics,Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070)
To obtain a multi-objective shortest path,which may meet the decision-maker's requirements,this paper presents the basis of syclic research k shortest path and constructs a polynomial algorithm to intersect the new set.After every round of the k shortest path searching,the algorithm preduces a multiobjective shortest path or alternative path by the intersection.When a number of alternative paths are available,the method of projection of Vague set and distance is used.The optional schemes are sequenced according to the evaluation size,thus the best optimal solution may be obtained.
multi-objective;k shortest path;Vague set
O122.6
A
1671-0436(2011)03/04-0025-03
2011-05-26
康太平(1986— )男,硕士研究生。
责任编辑:唐海燕
