支承形式对曲线梁桥的受力影响分析

肖 兵,方诗圣,肖 龙

(1.合肥工业大学土木与水利工程学院,合肥230009;2.中国建筑工程第八局,天津300000)

随着我国公路建设的蓬勃发展,曲线梁桥作为实现各方向交通连接的必要手段,应用越来越多.但曲线梁桥受力较复杂,具有以下一些特点:弯扭耦合效应明显,内梁和外梁受力不均,墩台受力复杂等[1].由于曲线梁桥的支座反力有外侧大、内侧小的倾向,在内梁中有产生拉力的可能,内侧支座会产生脱空现象.因此,支座的设置也直接影响到全桥的内力分布,设定合理的支承形式是保证曲线梁桥安全施工与使用的关键因素之一.

近年来,许多学者对曲线梁桥的支座形式作了一些研究,提出曲线梁桥在支座设置上应注意的问题.文献[2～3]对曲线梁桥进行了内力与变形的分析,得出合理的支点预偏心可以减小曲线梁桥结构的内力与变形,但没有对中支点也设抗扭支承的情况作分析.文献[4]以一四跨小半径曲线梁桥为例,分析不同支座布置形式下曲线梁桥支座反力与扭转变形,没有就扭矩作分析.文献[5]研究发现设置抗扭支座可减小曲线梁桥的扭矩,在独柱墩设置合理的支点预偏心可以减小扭矩以及端支座竖向反力之差.

然而现在研究多针对独柱点铰支承的跨径不大的曲线梁桥.对于联长较大(大于100 m)的曲线梁桥,仅在两端设抗扭支座时,弯桥抗扭跨度较大,会使上部结构内部产生过大扭矩,并不能有效改善全桥的扭矩分布.本文根据以上研究,对曲线梁桥在多种支承形式下的受力特征,以及曲率半径对曲线梁桥的影响做较全面的分析,并得出结论.

1 曲线梁桥分析方法

曲线梁桥目前常见的分析方法主要有两种:一种是解析法,它把弯桥模拟成一根单曲梁,采用纯扭转或约束扭转理论计算,横截面内力分析采用横向分布理论,概念清晰,计算简单,与直线桥分析方法类似,但该方法对于变截面、变半径弯桥的分析有较大困难.另一种是数值法,如有限元、有限条法等,单元形式主要有梁单元、板壳单元以及实体单元等,可以较精确模拟结构的受力行为[6].国内外学者对于分析结构的各种有限元法作了一定研究,得知梁有限元法在经济和技术上有许多优势[7].

目前工程中常用的曲线梁桥单元模型有几种:空间梁元模型,空间薄壁箱梁元模型,空间梁格模型,实体、板壳单元模型.空间梁元模型依据单纯扭转理论,即将弯梁桥结构当作集中在梁轴心线处的弹性杆件来处理,并认为受力后横断面仍保持平面,且截面周边形状保持不变,就可以将其离散为有限个空间直梁或曲梁单元.空间梁元模型简单,易于程序的实现,但要求桥梁宽跨比不应过大,一般当跨度为边肋或边腹板间距离的3～4倍时方可满足精度.本文实例的曲线梁桥宽跨比不大,故采用空间梁元模型.

2 工程实例

一座三联曲线梁桥,曲率半径为195 m,其中第一联和第三联的上部结构采用预应力混凝土现浇连续箱梁,跨径5×25 m;第二联上部结构采用先简支后连续预应力混凝土预制箱梁,跨径30+2×25+30 m.

2.1 有限元模型

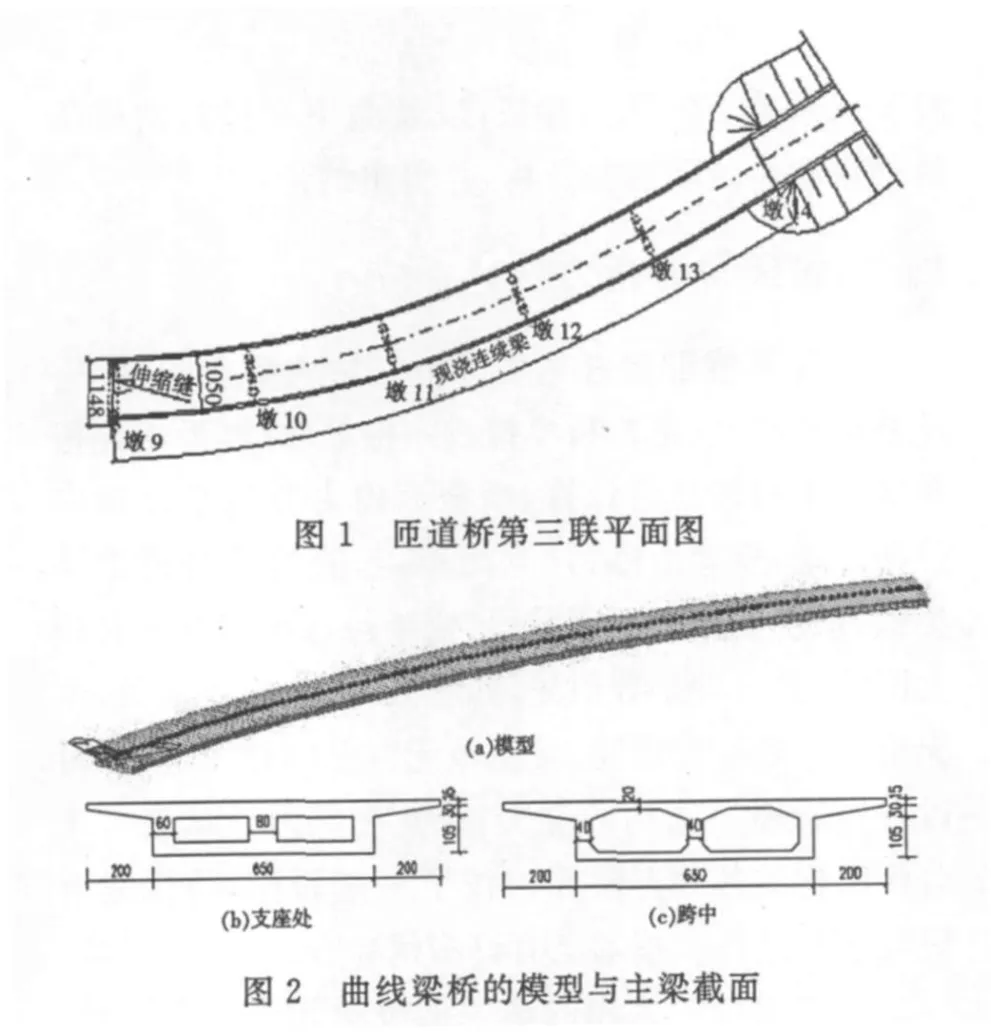
采用有限元软件Midas Civil对该曲线梁桥的第三联进行建模分析.第三联平面图见图1.主梁采用单箱双室截面,底面宽 6.5 m,桥面宽10.5 m,高1.5 m,模型采用梁单元,共划分为147个单元,见图2(a),支座处和跨中截面如图2(b)和图2(c)所示,图中尺寸均为cm.

2.2 支座布置形式

为了分析设置抗扭支座和支座预偏心对曲线梁桥受力的影响,初拟支承形式有如下四种,示意图见图3.有研究表明,中间墩顶支座固定对弯桥的受力与变形有利[8],故在11号墩顶限制其三个方向的线位移.

方案一:梁端设置抗扭支承,中间各墩顶设置点铰支承,不预设偏心距;

方案二:梁端设置抗扭支承,中间各墩顶设置点铰支承,预设一定的偏心距(墩10、11、12、13向外偏心0.10 m);

方案三:各墩顶均设置抗扭支承,不预设偏心距;

方案四:各墩顶均设置抗扭支承,预设一定的偏心距(墩 10、11、12、13向外偏心0.10 m).

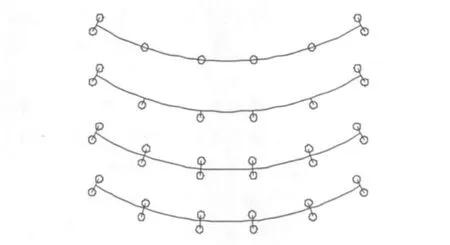
图3 支座布置形式示意图

2.3 计算结果与分析

荷载工况考虑以下几种:自重+二期恒载、预应力荷载、活载及几种荷载共同作用.其中活载包括车辆荷载和离心力的作用,其中车辆荷载分为偏外侧行驶和偏内侧行驶两种情况,均按照现行桥规取值.

2.3.1 不同支承形式对曲线梁桥扭转效应的影响

自重+二期恒载、预应力、活载以及组合荷载作用下引起曲线梁桥的主梁扭矩见图4.

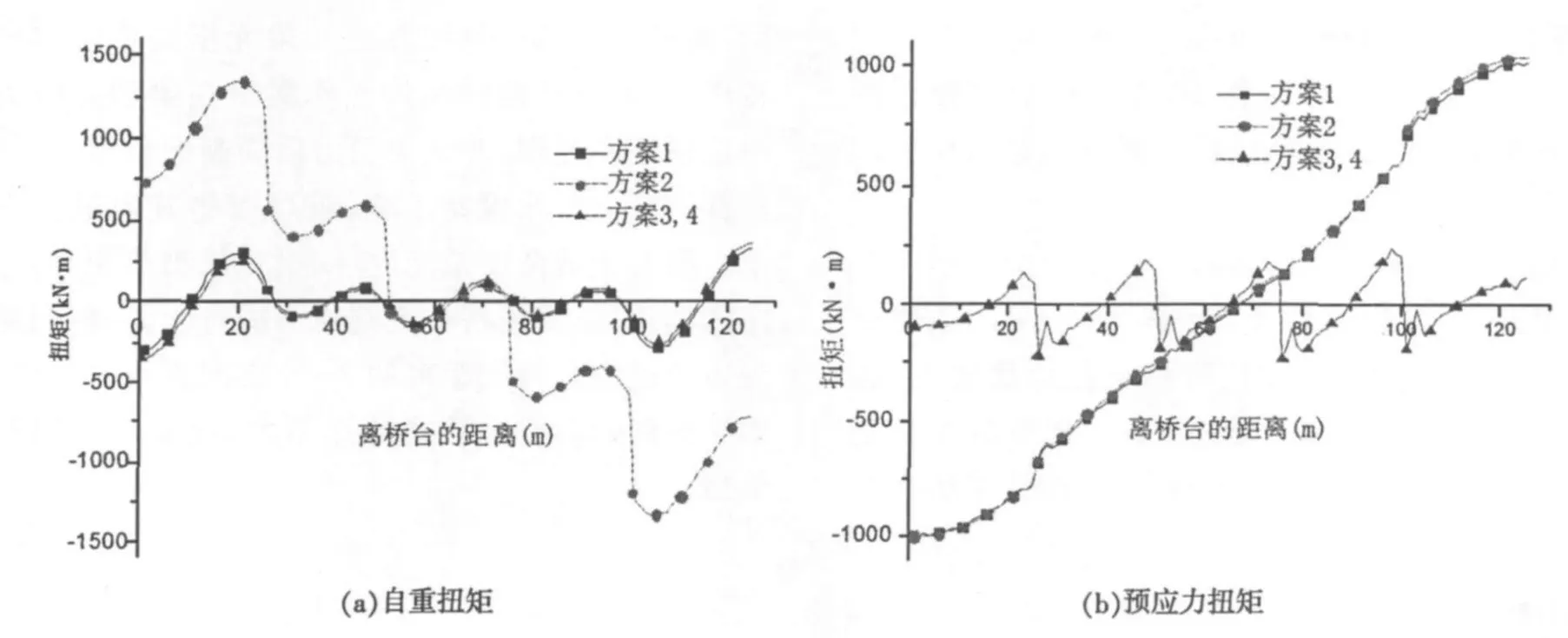
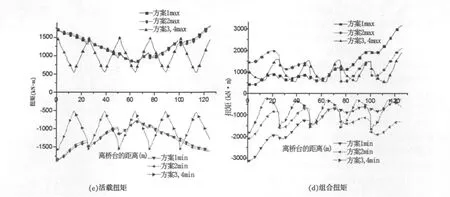
图4 不同支承形式的曲线梁桥扭矩

从图4可以看出,在两端抗扭、中间点铰支承时,支座预偏心对自重下的扭矩影响较明显,设置偏心后,与梁端处扭矩相比,中间支点处的扭矩绝对值增大,扭矩图发生一定的偏移;支座预偏心对预应力产生的扭矩影响不明显;设置偏心后,活载产生的扭矩变化也不大.而在全桥设置抗扭支承时,设置偏心前后的主梁扭矩不变.

中支点设置抗扭支承对自重产生的扭矩几乎无影响,但大大降低了预应力荷载引起的扭矩,也降低了活载引起的扭矩,组合扭矩在端部减小较多,从而明显改善了曲线梁桥的受力.

2.3.2 不同支承形式对曲线梁桥支座反力的影响

对上文四种支座布置形式下的曲线梁桥进行计算分析,分别得到支座竖向反力数值,比较结果分别见表1.研究表明,支座形式的改变对活载作用下支座反力几乎无影响,故仅列出自重、预应力及组合作用等工况下的结果.

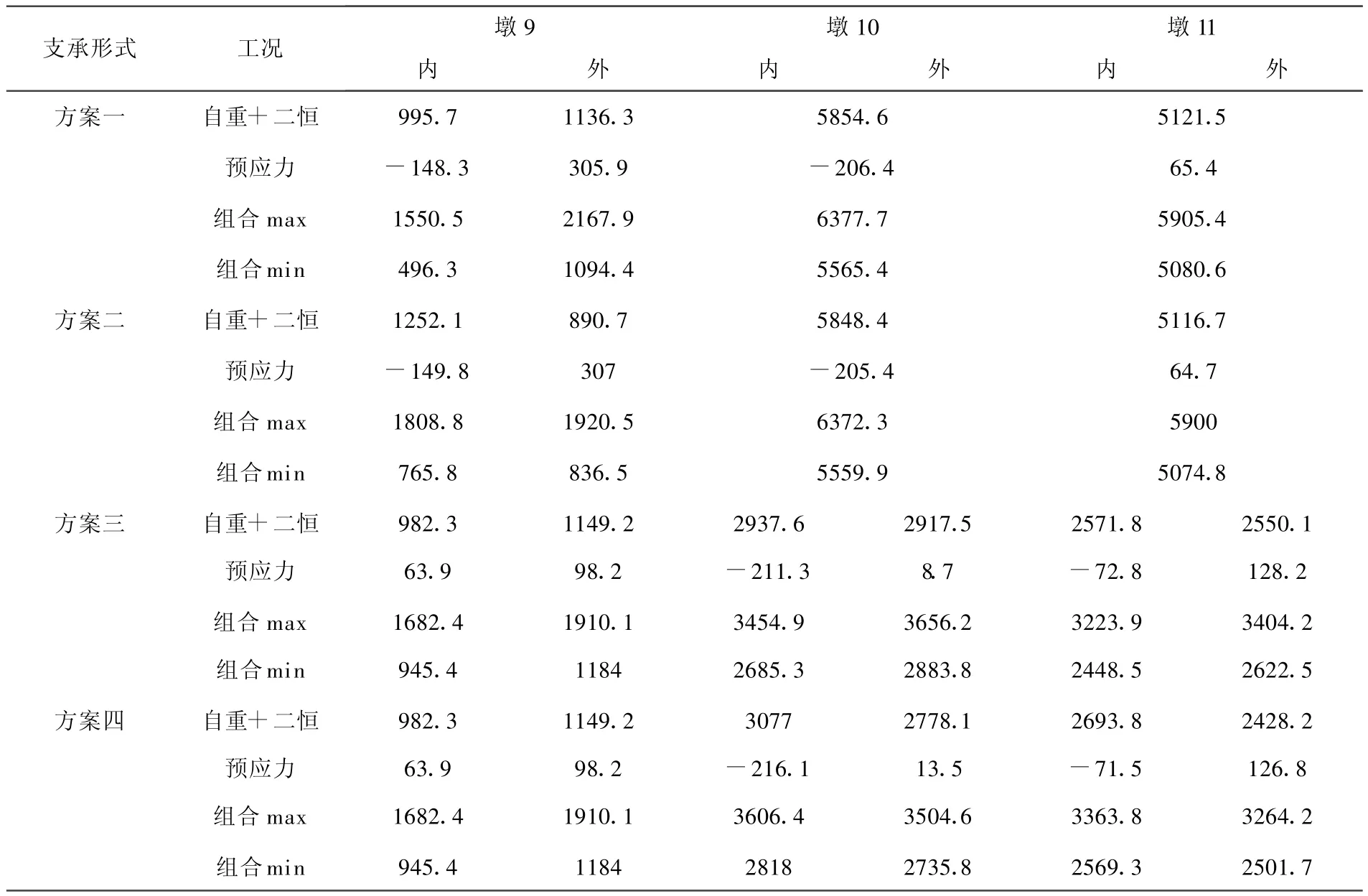
表1 不同支座布置形式下的支座反力(k N)

从表1看出,在未设置支座偏心的情况下,自重和预应力荷载的作用会使曲线梁桥内侧支反力小而外侧支反力大,在预应力作用下的内侧支反力则可能为拉力.在组合荷载作用下,内侧支反力与外侧支反力的差值较大.支座预偏心对自重+二期恒载作用下的支座反力影响较明显,设置偏心后,内外侧支座反力之和基本没有变化,但内侧支反力增大,外侧支反力减小,对于内外支座反力分配起到明显的重分布;由于预应力作用下的内侧支反力可能为负值,则支座预偏心可以有效地使自重+二期恒载和预应力联合作用下的内外侧支反力趋向均衡;在组合荷载作用下,内外侧支座反力趋向均衡.支座预偏心对预应力作用和活载作用下的支座反力影响并不明显.

在连续曲线梁桥中,中墩设置抗扭支座后,端支座内、外侧反力趋向均衡,各中墩内外侧的支座反力之和与单支座的反力相比基本没有变化.

2.3.3 曲率半径变化对曲线梁桥受力的影响

由上文的分析得知,全桥设置抗扭支座有利于改善曲线梁桥的内力分布.因此采用方案三的支座布置形式,改变曲率半径R进行分析.在荷载共同作用下,不同半径曲线梁桥的扭矩和竖向支座反力如图5和表2所示.

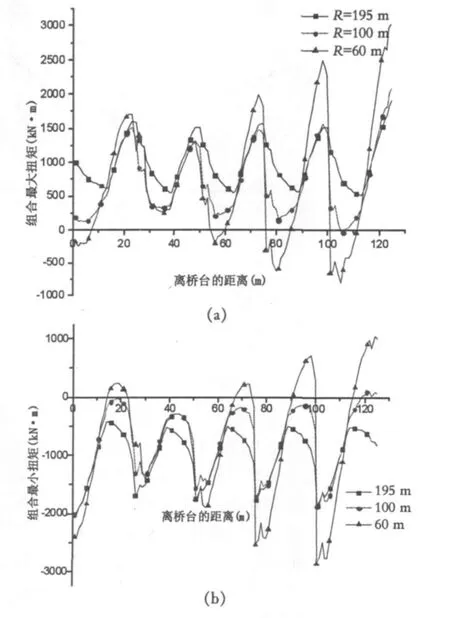
图5 不同半径曲线梁桥的扭矩

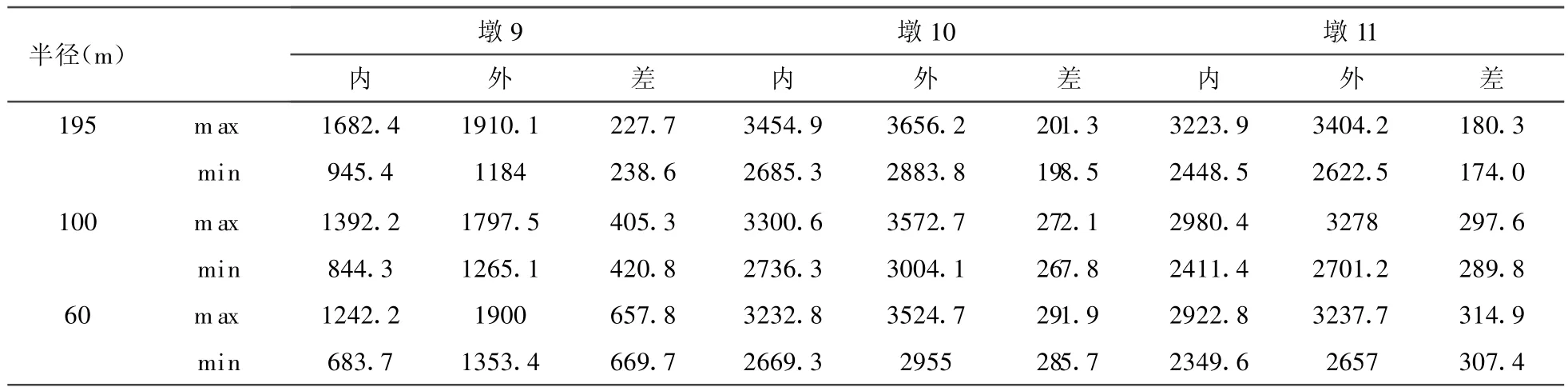
表2 不同半径曲线梁桥的支座反力(k N)

由图5和表2可以看出,曲线梁桥上部结构的扭矩随着曲率半径的减小而增大,且曲率半径愈小,其增幅愈明显;内、外侧支座反力之差也随着曲率半径的减小呈增大趋势.

全桥设置抗扭支座情况下,内侧支座均未出现拉力.由于中支点设置抗扭支座时设预偏心并不影响桥梁的扭矩分布,可以通过试算法得到合适的偏心值,以使曲线梁桥的内、外侧支座反力趋向均衡.

3 结论

本文对不同支承形式对曲线梁桥受力的影响进行分析,通过对计算结果进行比较可得出以下结论:

(1)两端抗扭、中间点铰支承时,设置偏心后,自重下的扭矩变化较大,预应力及活载下的扭矩基本无变化,组合扭矩减小;而全桥抗扭支座时,设置偏心对改善梁扭转效应的作用不大.中支点设置抗扭支座对自重下的扭矩几乎无影响,但降低了预应力和活载下的扭矩.

(2)设置支点预偏心和设置抗扭支座,都能使内、外侧支座反力趋向均衡.

(3)小半径是曲线梁桥的不利因素,半径越小,扭矩越大,支座反力之差越大.

(4)对于联长较大(大于100 m)的曲线梁桥,宜在全桥设置抗扭支座,以改善曲线桥的内力分布.

[1]邵容光,夏 淦.混凝土弯梁桥[M].北京:人民交通出版社,1994.

[2]朱金坤.独柱单点铰支承混凝土曲线梁桥的稳定性能研究[D].东南大学,2004.

[3]滕 军,胡 渝,郭时安,等.高墩小半径曲线梁桥支点预偏心时力学性能分析[J].工程抗震与加固改造,2009,31(2):9-15.

[4]康鸣雷.小半径钢筋混凝土曲线梁桥的支座设置[J].中国市政工程,2007,(6),32-35.

[5]黄 艳,亓路宽,孙国富.小半径预应力曲线连续梁桥的扭转效应研究[J].中外公路,2009,29(1):112-115.

[6]崔 婷.曲线预应力混凝土箱梁分析方法及程序设计[D].长安大学,2008.

[7]Wu Yaping.A Curved Box Beam Element Considering Shear Lag Effect and Its Static and Dynamic Applications[J].Journal of Sound and vibration,2002,253(5):1131-1139.

[8]许 莉,房贞政,洪 适.预应力混凝土曲线连续箱梁桥支座布置研究[J].南昌大学学报,2009,31(1):83-89.