基于CORDIC算法的多频激光测距系统性能分析

崔 炜，陈 磊，陈 宇

（长春理工大学 电子信息工程学院，长春 130022）

0 引言

目前，已经开发了各种各样的激光测距系统，主要应用于室内机器人，无损检测、侦查与安防以及汽车的智能巡航控制等方面[3]。除了三角法和干涉法以外还有脉冲法和相位法可以取代飞秒测量实现激光测距。相位法测距系统由于使用光外差技术，通过频率调制将比较短的时间间隔转化成为比较适合测量的相位差。因此，相位法激光测距系统作为高精度、非接触测量方法,在各种需要高精度距离测量或速度测量的领域中得到了广泛的应用[1,2]。但是，由于相位差的测量范围在0到2π之间,因此距离测量范围较小，为了解决这一问题，一般采用双频或多频调制，较低的频率满足测量范围的要求，而较高的调制频率可以得到较高的测量精度。所以只要采用合理的频率组合，就能既保证系统的测距范围又保证系统的测距精度。通常的相位检测方法有三种：过零检测法、相关分析法和频谱分析法。过零检测法大约有10%的测量误差，频谱分析法主要采用快速傅里叶变化等来分析回波信号的频率和相位从而得到相位差[4]，虽然其检测精度可以伴随着傅里叶变变换点数的增加而提高，但是随之而来的是大量的乘加运算，降低了系统的工作效率。本文提出了一种正交相位检测和CORDIC角度解算方法，能够有效地提高距离测量精度并大大降低系统的运算量。CORDIC（Coordinate Rotation Digital Computer)的是一种数值逼近方法,其基本思想是：用一系列固定角度的不断偏摆逼近所需旋转的角，从广义上讲它是一个数值逼近的方法，由于这些固定的角度与计算基数有关，运算只有移位和加/减。本文主要利用CORDIC算法求反正切函数，最终得到相位延迟[4]。

1 系统总体设计

基于CORDIC算法的多频调制实时激光测距系统的原理如图1所示，主要由FPGA实现的信号处理部分、数字域模拟域变化处理电路和激光头等三部分组成。工作原理是：FPGA内部DDS产生三路正弦信号f0、f1、f2，叠加后由DA输出对种子光进行调制，调制后的激光信号通过光学系统在目标上产生回波信号。接收系统接收到目标反射的回波信号以后将其与种子光混频，再由光电转换和低噪声放大器得到中频信号，中频信号经过模数转换、数字带通滤波器选频后得到带有相位延时的数字域正弦信号 f0'、f1'、f2'，它们分别与本地的 DDS1’、DDS2’、 DDS3’产生的与 f0、f1、f2同频且已知初始相位的三路信号作为本地信号， f0''、f1''、f2''作正交运算后得通过CORDIC角度解算模块得到角度值，最后由距离解模糊模块得到被测距离。

2 距离信号的解算

目标回波在接收端经低通滤波后得到的归一化信号为：

图1 高精度多频调制实时激光测距系统

式（1）信号通过选通滤波器后可以得到：

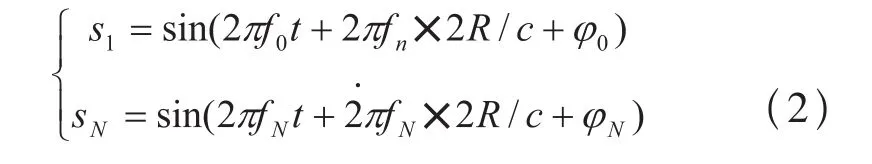
这些信号分别通过同相正交环鉴相电路就可以得到各自的相位延迟正切函数

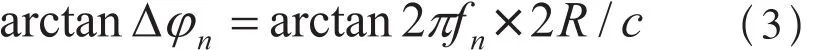
在通过反正切运算，即可得到相位延迟Δφn＝2πfn×2R/C，解模糊之后可得到距离信息，原理如图2所示。若中频输入信号为：

其中fc为载波频率，本地DDS的同相与正交支路的信号分别为：

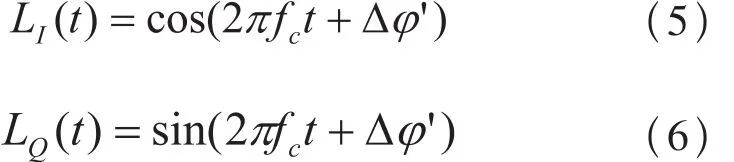
Δφ'是中频信号和DDS信号之间的瞬时相位差，混频后同相、正交支路的输出分别可以表示为：

将同相正交分量分别输入到CORDIC的X0和Y0端，并过n次迭代之后可以得到：

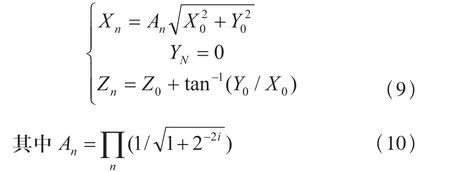
如果相位累加器的初始值为0，则Zn＝tan-1（Y0/ X0），即输出为X0和Y0的反正切值，从而求得了相位延迟。

3 CORDIC截断误差分析

在CORDIC算法中，由于运算中的数据截断会引起相位计算的误差，旋转迭代过程中，令

定义Q[.]为量化操作，则

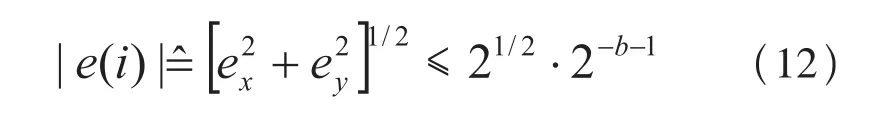
在CORDIC运算中，截断误差主要包含两个部分：当前计算单元的截断误差和之前计算单元的截断误差的积累，定义f (n)角度解算过程中所产生的全部截断误差，则有：

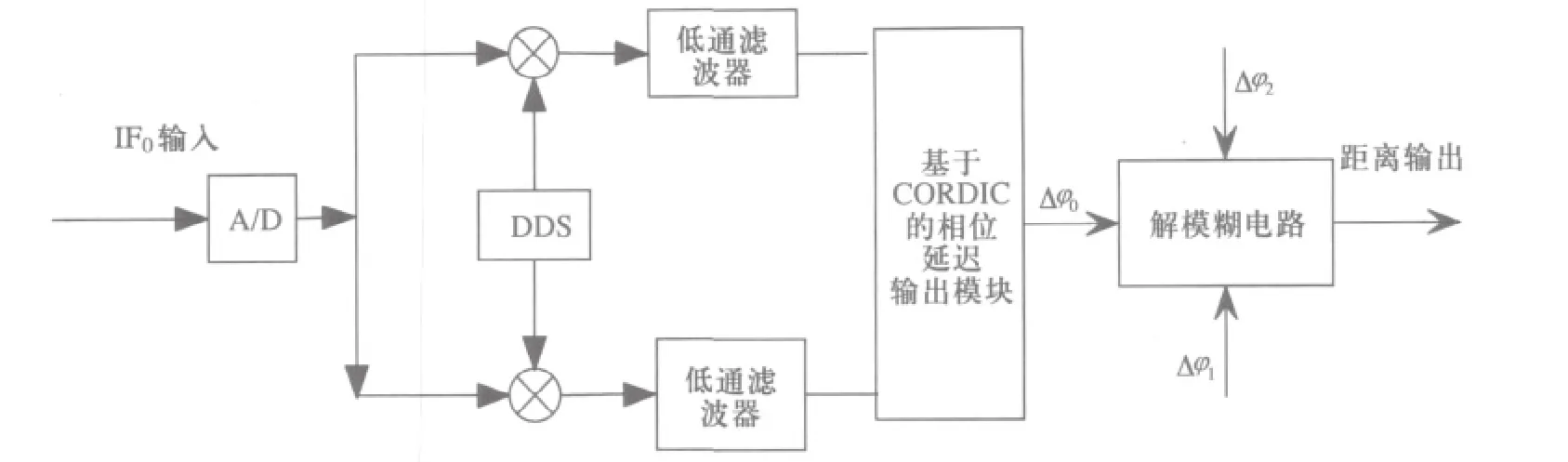
图2 基于数字COSTAS环的角度解算原理

则根据公式（8）、（9）可得

由式（14）可知，截断误差的大小与X、Y有关，数据位数越大，输出误差越小，并成2的负指数减小，通常CORDIC迭代次数大于十次，常数C小于等于2，如果X、Y和输出Z的位数均取16位则CORDIC算法的截断误差很小。测距系统的主要误差来源是噪声引起的回波信号相位不确定。

4 结论

基于CORDIC算法的激光测距系统中，系统测量误差的主要来源是噪声引起的回波信号相位不确定。在数字域可以通过低通滤波，积分清洗滤波器的限制噪声提高信噪比的方法来改善。本文测距系统中测量信号最大频率为100MHz，与本地已知初始相位差的100MHz信号经过正交计算得到相位延迟的正切值，再通过CORDIC相位解算模块解算出角度值，当回波信噪比SNR=14dB时，角度测量误差为0.0264°，对应的距离测量误差是0.11mm。当回波信噪比提高时，系统的测量误差会进一步降低，通过测试计算，在回波信噪比达到20dB时，角度测量误差可以达到0.01°。

[1] Yang Fu, He Yan, Chen Weibiao. Parameter design of space-borne laser altimeter[J].Acta Optica Sinaca, 2008,28(3): 573-577.

杨馥, 贺岩, 陈卫标. 星载激光相干测高计的参量设计[J]. 光学学报, 2008, 28(3): 573-577.

[2] Jia Zhexin, Gong Ke, He Shufang, et al..High-speed Flyer Velocity measurement system based on laser scattering [J].Chinese J. Lasers, 2008, 35(7): 1050-1054.

贾哲新, 巩轲, 何淑芳, 等. 基于激光散射的高速微粒测速系统[J]. 中国激光, 2008, 35(7): 1050-105.

[3] Stephae Poujouly et al A twofold modulation frequentcy laser range finder journal of optics 2002 s356-s363.

[4] Jia Fangxiu1, Ding Zhenliang, Yuan Feng1, Ge Dongshen,Real-Time Laser Range Finding System for Moving Target Based on All-Phase Fourier Transfrorm Spectrum Analysis [J]. Acta Optica Sinaca, 2010, 30(10): 2829-2834.

贾方秀, 丁振良, 袁峰, 葛东升. 基于全相位快速傅里叶变换谱分析的激光动态目标实时测距系统[J]. 光学学报, 2010, 30(10): 2829-2834.

[5] HU Y H. The quantization effects of the CORDIC algorithm [J]. IEEE Transactions on Signal Processing,1992, 40(4): 834-844.

[6] GAO Jinzhan. 微弱信号检测[M]. 清华大学出版社.

[7] KOTA K, CAVALLARO J R. Numerical accuracy and hardware tradeoffs for CORDIC arithmetic forspecialpurpose processors [J].IEEE Transactions on Computers,1993, 42(7) : 769-779.

[8] OPPENHEIM A V, WEINSTEIN C J. Effects of finite register length in digital filtering and the fast Fourier transform [J]. Proceedings of the IEEE, 1972, 60(8) : 957-976.