基于光照子空间的人脸识别研究
2011-07-06李思明刘笃晋孙淑霞丁照宇
李思明 刘笃晋 孙淑霞 丁照宇
(1.成都理工大学 信息科学与技术学院,成都610059;2.四川文理学院 计算机科学系,四川 达州635000)
目前,在可控光照、用户配合条件下的人脸识别技术已经相当成熟。但在非理想条件下(如光照可变、姿态可变、部分遮挡、表情变化等)的人脸识别却尚待提高。其中光照问题的影响尤为严重,研究发现由于光照的不同给人脸图像带来的变化超过了不同人脸图像之间的变化。针对光照变化问题,目前有多种思路,其中基于模型的方法取得了较大的成功。
在基于模型的方法中,光锥体法[1]是第一次从理论上把光线和姿态问题同时解决的算法,而且在光照问题上同时考虑了自身阴影和投影阴影。在剧烈的光线变化下,光锥法的识别率甚至超过了当时所有的方法。但是在通常的情况下,由于需要的目标物体在极端光照条件下的图像数量是巨大的,因而很难准确地建立目标物体的光照锥,而在实际的应用过程中不需要也不可能建立一个完备的光照锥。基于球谐函数理论和信号处理方法,Ramamoorith[2]以及 Basri[3]分别提出了凸的朗伯反射体的光照空间可以利用一个9维的线性子空间来近似,并且称该子空间为谐子空间;也就是说,对于所有的人脸都存在9种确定的虚拟光照状态,每个人在这9种光照状态下采集到的9张图像——谐函数图像(harmonicimages)组成的谐子空间H都可以作为对于其光照锥的一个低维近似。但是在得到谐函数图像之前,需要已知目标物体的表面法向量和反射率;而法向量与人脸三维结构有关,为求得三维结构,一般要进行三维人脸重建。目前有很多种方法,从算法的复杂性、识别效率以及最终识别率来看,有2种比较有代表的方式,一种是将平均3D人脸变形到特定人脸,另一种是用中性人脸形状与特定人脸相对应。这2种算法中,前一种重建的算法过程比较复杂,精度较高;后一种算法相对简单,但精度不够,影响了最终的人脸识别率。
本文所用算法只计算了典型的特征点深度值,计算量明显减少,以特征点定位利用NURBS技术实现三维人脸重建。此算法不仅较简单而且精度较高,克服了前2种算法的缺点。
1 人脸特征点深度的计算
为了求得人脸的三维结构,首先要选取有典型代表性的特征点,然后求出其深度。本文参照MPEG-4中人脸特征点及结合算法要求,经实验选取了如图1所示的33个特征点(非 MPEG-4上的点采用与相邻特征点位置来决定)。

图1 标定的人脸上特征点Fig.1 The calibrated human face feature points
为了求出人脸特征点深度,首先要知道图像是如何形成的。在球面谐波理论中,Basria和Ramamoorthi指出,假设物体为朗伯凸表面,则图像的灰度由光源方向和表面法向量共同决定,如:
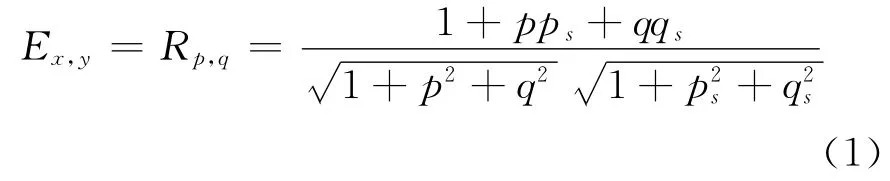
式中:Ex,y是图像点(x,y)处的灰度;Rp,q是该点反射函数;而(p,q)是表面梯度;(ps,qs)表示光源方向,其定义为

其中σ和τ分别是光源的倾角和俯角。
从(1)式求解图像点深度z,即所谓的求SFS问题。SFS问题是一个病态问题,需要引入一定的约束条件,将其转化为一个正则化的问题。由于人脸是较为光滑的表面,其表面反射函数的高阶分量较小,线性化的处理不会带来很大的误差,同时又有计算时间上的优势。因此,本文采用Tsai和Shah的线性化的方法,将其进行正则化,采用文献[4]中的方法求解,首先离散化反射函数,令:
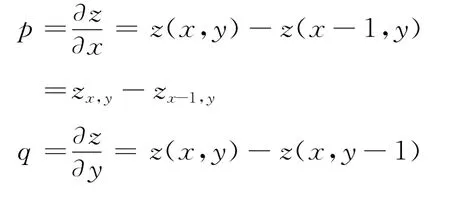
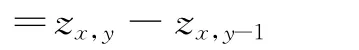
这样,将(1)式表示为:
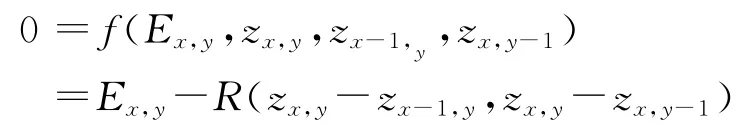
对一个像素点(x,y)和给定图像E,函数f关于深度zn-1(进行第n-1次替代得到的深度值)进行一阶Talyor展开,若一幅N×N的图像,就有N2个方程,形成了一个线性方程组,然后通过Jacobi替代法解此方程,简化整理得:

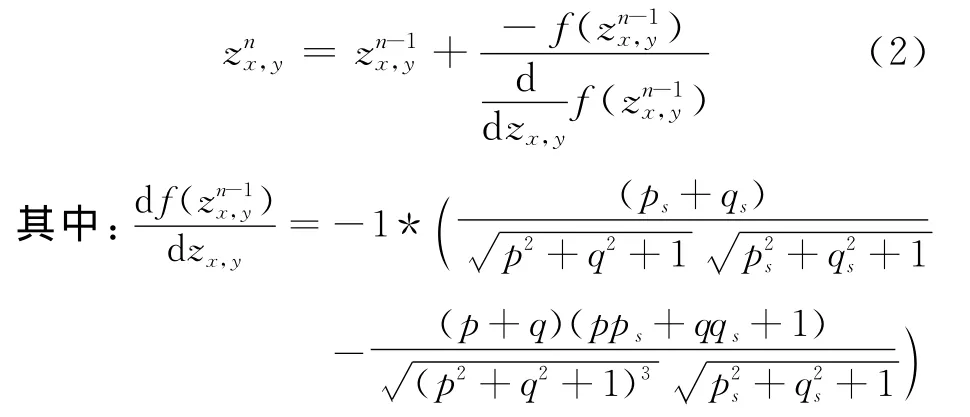
假设初始深度估计z0x,y=0,代入(2)式并不断迭代至收敛,即得最后SFS的结果。由人脸正面照片通过SFS恢复的三维人脸的特征点深度,在眉毛眼睛嘴巴鼻子部位的深度不太正确,然后用文献[5]的方法,可以得到准确的人脸特征点深度。
2 散乱数据的NURBS曲面拟合
前面获得的只是大量散乱的三维空间点,并没有空间结构信息,要生成一个具有较好表达能力、信息更加丰富的人脸曲面模型,需要进行曲面拟合。基于散乱数据点的曲面生成问题,普遍存在重建运算量大、算法过程复杂、求出的曲面精度难于控制等问题;并且当测量数据存在噪声时,曲面质量很难保证。基于B样条的方法,在构造参数曲面时用的是逐步逼近,因而存在造型不便且影响精度的现象。随着NURBS理论的日趋成熟,特别是权因子与参数化问题研究取得了实质进展,因而可以用NURBS曲面精确地表示人脸表面曲面,并且自由度因子使人脸表面曲面形状的控制和修改更加精确,使生成的三维人脸更逼真。
2.1 非均匀有理B样条曲线和曲面的定义
一条k次NURBS曲线可以定义表示为一分段有理多项式函数[6]:
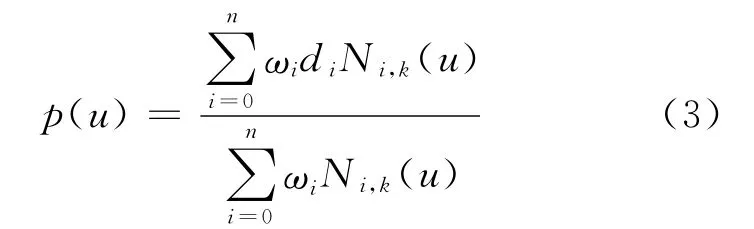
其中:ωi(i=0,1,2,…,n)称为权因子或权,分别与控制顶点di(i=0,1,2,…,n)相联系。首末权因子ω0,ωn>0,其余ωi≥0,且顺序k个权因子不同时为0,以防止分母为零、保留凸包性质及曲线不致因权因子而退化为一点。Ni,k是由节点矢量U=[U0,U1,…,Un+k+1]按德布乐 -考克斯递推公式决定的k次规范B样条基函数,定义域u∈[uk,un+1]=[0,1],图2为其插值示意图。
图2 NURBS插值示意图Fig.2 NURBS interpolation diagram
2.2 NURBS三维人脸重建算法
利用前面所求的人脸特征点深度,以2.1节中非均匀有理B样条曲线的定义为基础,用非均匀有理B样条曲面上点的德布尔算法推广来计算NURBS曲面上的点。与NURBS曲线一样,对NURBS曲面的2个参数方向的节点矢量直接插入节点是不实际的。由于节点不具有清楚的几何意义,因而采用将NURBS曲线反插节点推广到曲面的技术,即采用将控制顶点插入控制网格,然后反算出要插入的节点。NURBS曲面插值过程是根据给定曲面上的一组点φij(i=0,1,…,n;j=0,1,…,m)构造满足P阶连续的NURBS曲面,使曲面经过前面所求的定点。一张k×l次NURBS曲面以有理分式形式表示为
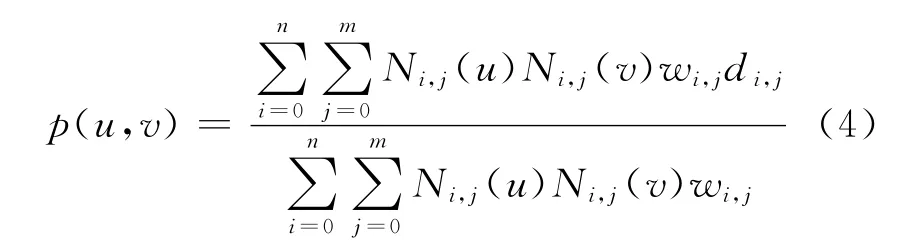
其中:Ni,j(u)为u方向的k次规范B样条基函数,Ni,j(v)为v方向的l次规范B样条基函数,他们分别由u向与v向节点矢量U=[u0,u1,…,um+k+1]和V=[v0,v1,…,vn+l+1]按德布尔公式决定,wi,j是与顶点di,j联系的权因子,di,j为控制点(i=0,1,2,…,m;j=0,1,2,…,n)呈拓扑矩形阵列,形成一个控制网格。从(5)式可知,NURBS曲面在计算控制点矩阵后步骤如下:
Step 1:计算插值曲线和公共节点矢量U;
Step 2:插入控制点;
Step 3:计算节点矢量d;
Step 4:构造曲面。
3 球面谐波基图像的光照估计
球面谐波子空间理论表明,在各向同性远光源假设条件下,朗伯凸表面的任意图像均可表示为该凸表面9个球面谐波基图像的线性组合,这9个线性组合的系数为光照系数,也就是说只要找到人脸图像这9个球面谐波基图像的线性组合,就可以表示出人脸图像,从而可以进行人脸识别。
人脸球面谐波基图像原理假设人脸为郎伯凸表面,其亮度公式为:
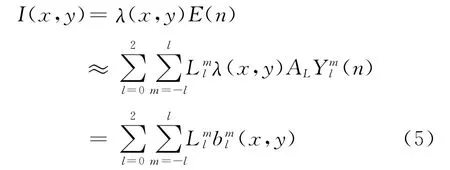
其中:λ(x,y)为某点的反射率;n为点(x,y)的法向量;E(n)表示辐照度,具体为:
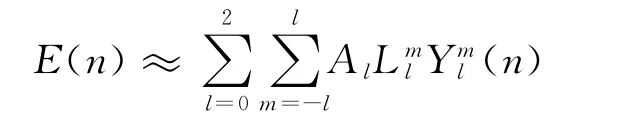
其中:Al为郎伯反射函数的球面谐波系数;为光照的球面谐波系数;为球面谐波函数。人脸球面谐波基图像为:
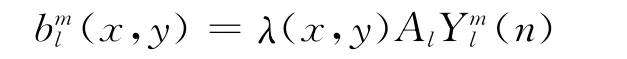
对9个光照系数进行调整,根据输入的图像产生9个光照不同的数字人脸。由于人脸的皮肤颜色大致相同,人脸每点的反射率λ(x,y)可以当作常值。根据2.2中求得的三维人脸曲面,采用文献[7]中的方法求出人脸表面法向量n,可以求出球面谐波基图像,通过最小二乘法解出9个光照系数,就可表示出人脸图像了。
4 实验结果及分析
4.1 实验前后人脸图对比分析
为获得较好的效果,本实验采用了光照补偿的方法作为人脸识别的预处理,尽量提高人脸识别率,经过采用文献[8]提出的纹理图像方法消减光照的影响后,根据本文实验方法所得实验结果如图4。从实验结果的图3和图4对比可以看出,图4的三维人脸的立体感非常明显,很好地恢复了图3中的单张二维照片的三维人脸,结果真实感也较强。
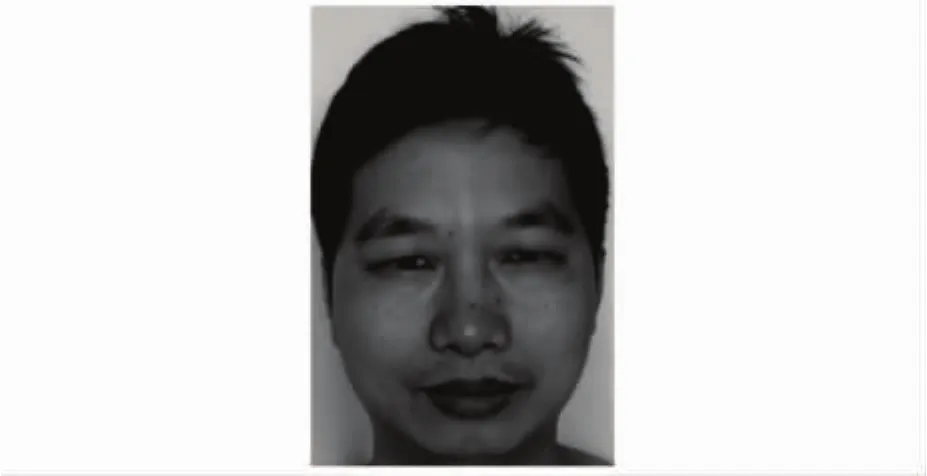
图3 重建前的人脸Fig.3 Face before the reconstruction

图4 重建后的人脸Fig.4 Reconstructed face
4.2 实验结果数据分析
本文选用常常用来进行测试光照情况的Yale B人脸库。此库有10个人的5760幅640×480的灰度图像,每个人都有9种姿态,每一种姿态包括64张光照条件不同的图像,选择的原则是原图和测试图之间只有光照的变化,根据拍摄时光源与镜头所成的角度大小,将此人脸库分成5个子集合:①0°~12°为集合Ⅰ;②13°~25°为集合Ⅱ;③26°~50°为集合Ⅲ;④51°~77°为集合Ⅳ;⑤78°以上为集合Ⅴ。对人脸进行归一化处理后,为了减少运算量,用PCA算法进行降维处理,采用图像相似性的最近邻方法识别。把比较接近正面光照的集合Ⅰ看成正常光照作为训练集,其余4个集合作为测试集。通过对平均3D人脸变形到特定人脸的方法[8](简称平均到特定法)和中性人脸的形状与特定人脸相对应的方法[9](简称中性特定法)以及本文方法进行对比实验,从表1中的测试结果可以看到,子集Ⅱ中的识别率都是100%,但集合Ⅲ、Ⅳ、Ⅴ中开始体现出了本文方法优越性,集合Ⅲ中本文方法比前两种方法分别提高了4.5%和2.2%左右,集合Ⅳ中本文方法比前两种方法分别提高了14.4%和8.1%,集合Ⅴ中本文方法比前两种方法分别提高了23.1%和17.6%。从本实验结果来看,本方法确实提高了人脸识别率。

表1 在Yale B人脸库上的识别率比较The recognition rate comparison in the Yale B face database
5 结论
基于光照子空间理论,本文采用一种新的方法重建了三维人脸,为减少计算量又利用文献[7]中的方法求得特定人脸的法向量,并进行了实验。从实验结果来看,提出的基于球面谐波基图像的人脸识别方法是可行且有效的,从识别率来看,结果是令人满意的。但本文方法还存在一些问题需要进一步研究,一是在光照影响很严重的情况下,如何将纹理特征很好地显示出来,二是通过NURBS技术重建的三维人脸要经过处理,如何解决处理方法对精度的影响也是下一步研究要解决的问题。
[1]Georghiades A S,Belhumeur P N,Belhumeur,et al.From few to many:illumination cone models for face recognition under variable lighting and pose[J].IEEE Trans:Pattern Analysis and Machine Intelligence,2001,23(6):643-660.
[2]Ramamoorith R,Hanrahan P.A signal-processing framework for inverse rendering[C]//Proceedings of SIGGRAPH,2001:117-128.
[3]Basri R,Jacobs D.Lambertian reflectance and linear subspace[J].IEEE Trans:Pattern Analysis and Machine Intelligence,2003,25(2):218-233.
[4]Tsai P S,Sshah M.Shape from shading using linear approximation[J].Image and Vision Computing,1994,12(8):487-498.
[5]Castelan M,Hancock E R.Acquiring height data from a single image of a face using local shape indicators[J].Computer Vision and Image Understanding,2006:64-79.
[6]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[7]王华兵,刘伟军,卞宏友.二维流形三角网格模型顶点法矢量估计[J].小型微型计算机系统,2009,30(7):1437-1440.
[8]卿来云,山世光,高文,等.基于球面谐波基图像的任意光照下的人脸识别[J].计算机学报,2006,29(5):760-768.
[9]刁显峰,王国胤,龚勋.一个改进的球面谐波模型及其在光照人脸识别中的应用[J].重庆邮电大学学报:自然科学版,2008,20(4):457-461.
