小子样试验均方根统计的修正方法

赵圣占，马擎宇

(92941部队96分队，葫芦岛125000)

0 引言

对于昂贵的武器试验来说，为了缩短试验周期和降低试验成本，往往是小子样的［1］［2］。这时均方根统计应十分谨慎，不能简单应用贝塞尔公式，而必须进行修正，应有一个大于1的修正系数。本文针对小子样试验，均方根估值 S1=两种情况，进行理论上的推导，得到两个修正系数公式，并给出相应修正系数的数据表，为小子样试验均方根统计的修正提供参考。

1 估值S1的修正方法

小子样武器试验时，特别要关注估值的无偏性［3］［5］。尽管的无偏估计值，即有σ2，但S2不是σ无偏估值，而是有偏的。同样，S1也不是σ无偏估值。现加以证明，并推导出其无偏估值。

为寻求S1的无偏估值，应先考虑其概率密度［4］，因为统计值S1的概率密度为：

式中，Kn－1为χ2的n－1个自由度分布密度，且Kn(x)的表达式为：

由此可见，S1不是σ无偏估值，据此容易导出均方根的无偏估计为：

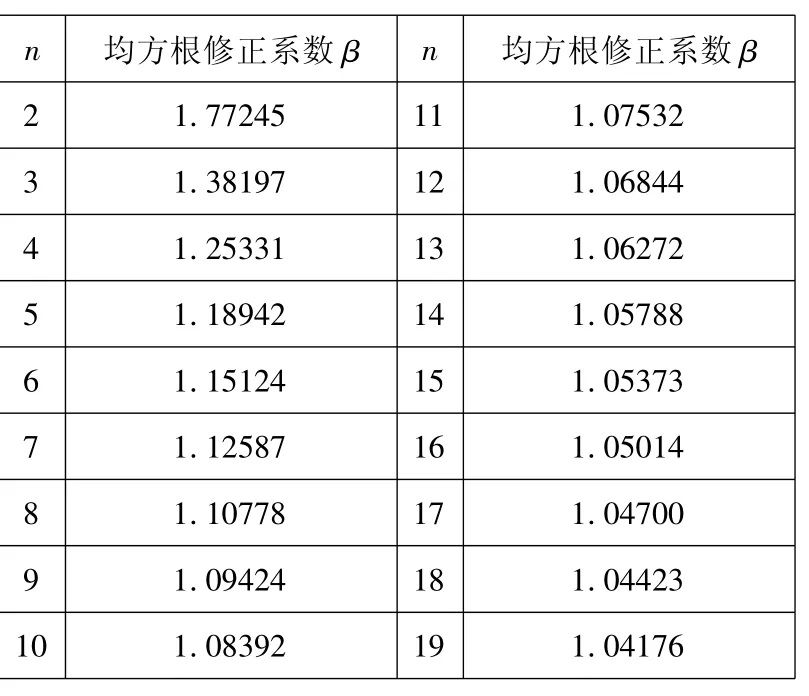
表1 S1修正系数的数据表

2 估值的修正方法

欲求E［S2］，不必再用概率密度的方法进行繁琐推导，可直接利用式(1)和S1与S2的关系。

因为

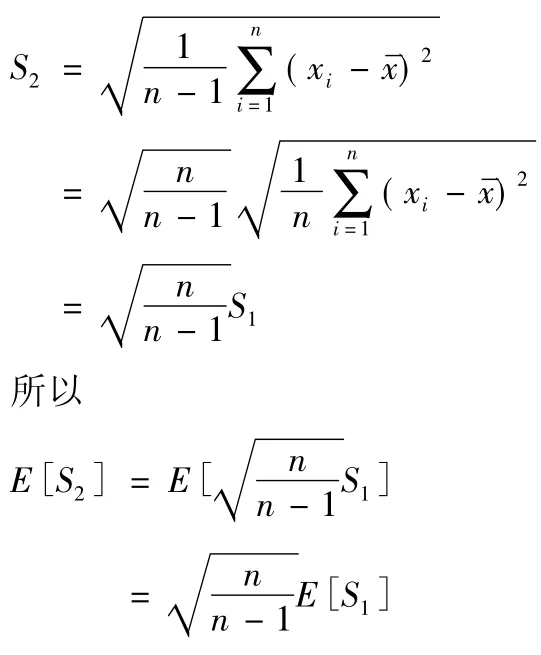
将式(1)代入得：

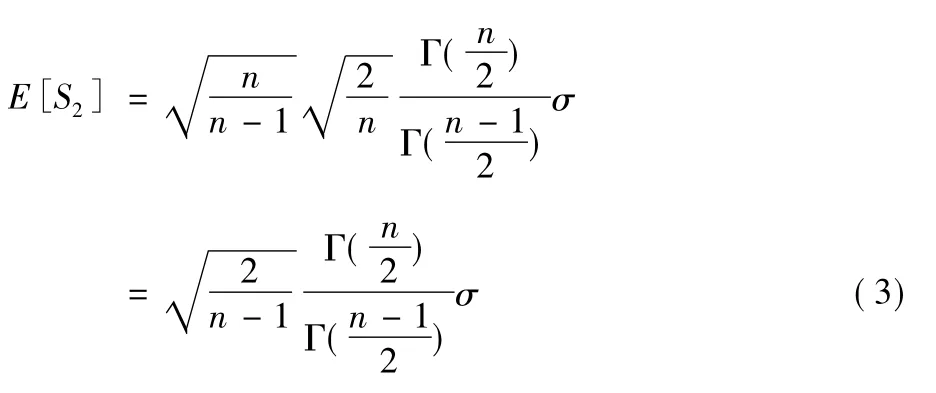
同理，均方根的无偏估计值为：

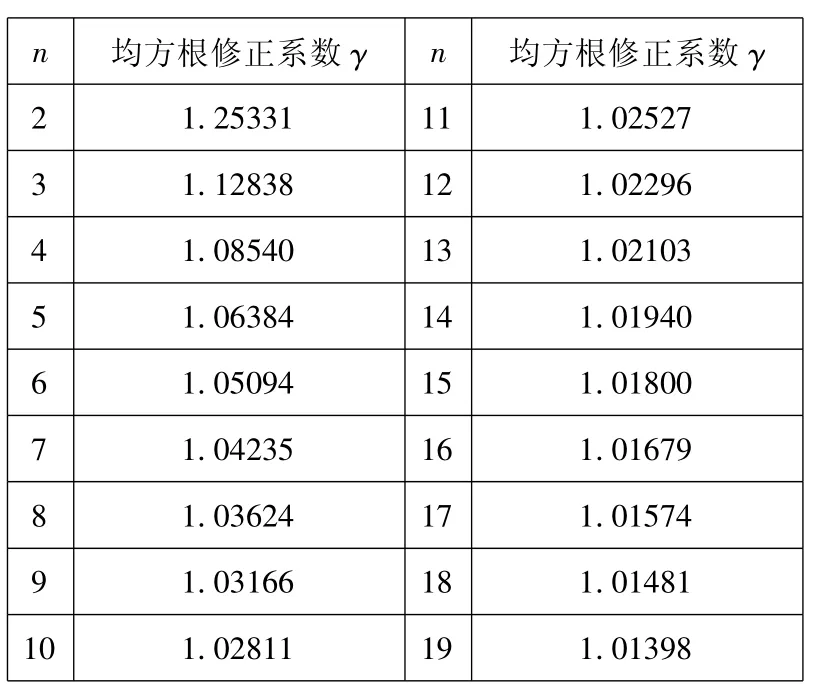
表2 S2修正系数的数据表

3 结束语

对于小子样试验来说，均方根估值不论其分母为n或n－1，均需要用表中β或γ作适当修正，才会取得较好效果。从两个数据表中不难看出：β大于γ，均大于1，且随着n的不断增大，β和γ不断变小，并无限趋近于1，即大子样情况下不需要修正。从工程物理概念上理解，小子样情况下，大误差一般出现几率较小，故统计的均方根往往比真实值要小些，n越小，越要考虑修正问题。

［1］李明，刘澎.武器装备发展系统论证方法与应用［M］.北京：国防工业出版社，2000：12-19.

［2］唐雪梅，张金槐，邵凤昌，等.武器装备小子样试验分析与评估［M］.北京：国防工业出版社，2001：23-26.

［3］李贤平.概率论与数理统计［M］.上海：复旦大学出版社，2003：15-18.

［4］汪荣鑫.数理统计［M］.西安：西安交通大学出版社，1986：34-36.

［5］杨榜林，岳全发.军事装备试验学［M］.北京：国防工业出版社，2002：42-47.