数控铣削参数优化的研究
2011-07-03耿金萍郭亚彬
耿金萍,高 顶,郭亚彬
(中国矿业大学 机电工程学院,徐州 221116)
0 引言
在数控加工中,数控程序的优劣不仅决定着零件的精度和形状,而且对数控机床的加工效率起着决定作用。目前,数控程序中的切削参数值(如铣削加工中进给速度vf和主轴转速n)的选择通常比较保守,这在很大程度上制约了数控机床的性能的充分发挥。据美国肯纳公司调查的数据显示:美国制造业所选用的切削速度值只能达到最佳切削速度的58%,刀具也只发挥了38%的功效,切削参数的不合理选择大约造成每年高达一百亿美元的浪费。为此需要改进传统加工方式的不足,提高机床的利用率。
对于曲面铣削加工,约束条件大部分都是非线性的,利用一般的求解方法都有一定的困难。切削手册或切削数据库主要适用于已知切削用量的情况,由于加工过程中的切削用量一般情况下是未知和变化的,所以数据库就难以直接提供优化参数,因此对加工参数的优化具有重要意义。基于软件仿真的加工过程离线优化的基本思想是实际加工前利用加工仿真来“识别”加工过程中的切削参数,在对加工过程中的性能指标如切削功率、切削力、表面粗糙度、机床转速范围等,结合优化目标的数学模型和非线性约束条件,从而优选出切削参数的最优组合达到优化的目的。
1 以最大生产率为目标的非线性数学模型
在批量生产时完成一道铣削加工的工时为
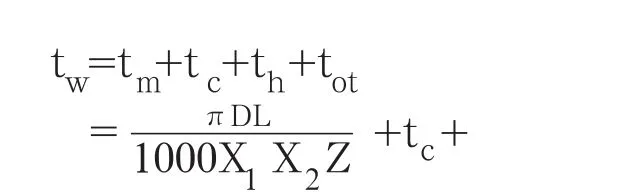
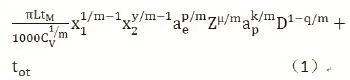
数学模型中的 x1和x2分别代表铣削速度θf和每齿进给量fz,tm是工序的切削时间,tc是工序之间的换刀时间,th是刀具磨损平均一道工序的换刀时间,tot是除了换刀时间以外的其他辅助时间,D是刀具的直径,L是切削长度,Z是刀具齿数,tm是刀具磨损的换刀时间,ae是切削宽度,ap是背吃刀量,Cv、m、y、p、μ、k、q是刀具的寿命系数。
2 约束条件
在切削过程中可能产生的约束是多种多样的,很难把所有情况都详细讨论,主要从机床功率、主轴转速、每齿进给量等等去考虑,因此,目标函数应该满足以下的条件约束。
1)切削速度的约束

2)每齿进给量的约束

3)切削进给力的约束

XF、CF、yF、μF、qF、ωF、KFc都是切削力系数,Ffmax是机床主轴最大进给力。
4)切削功率的约束
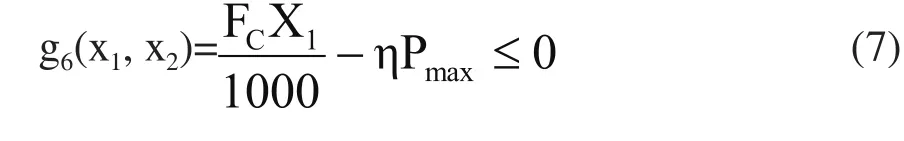
Fc是切削力,Pmax是机床的最大功率,η是机床有效系数。
5)零件表面粗糙度的约束

Rε是刀具刀尖半径,Rmax是最大表面粗糙度。
以上可以归结为在满足约束条件的情况下,求目标函数的最小值
即
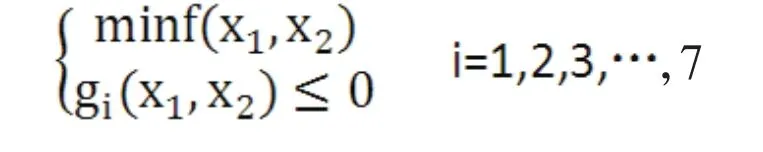
3 遗传算法在机械工程上的应用
利用遗传算法求解机械设计最优化问题,首先应对可行域中的点进行编码,然后在可行域中随机挑选一些编码组作为进化起点的第一代编码组,并计算每一个解的目标函数值,也就是编码的适用度,然后利用选择机制从编码组中随机选择编码作为繁殖过程前的编码样本。选择机制应保持适应度较高的解保留较多的样本,而适应度较低的解保留较少的样本,甚至被淘汰。在接下去的繁殖过程中,遗传算法提供了交叉和变异两种算子对挑选后的样本进行操作,交叉算子交换随机挑选的两个编码的某些位,变异算子则直接对一个编码中随机挑选的某一位进行反转,这样通过选择和繁殖就产生了下一代编码组,重复上述过程,直到结果满足约束条件为止。进化过程中最后一代最优解就是利用遗传算法解决最优化问题得到的最终结果。
遗传算法采用适用度函数值来评价个体性能并指导整个搜索过程而基本不用搜索空间的知识,对于一般的优化问题其数学模型为其中gj(x)为不等式约束,hk(x)为等式约束。

4 实例
铣削加工正弦曲面,采用整体式硬质合金球头立铣刀,直径10mm,刃数为2,工件为45钢,σb=650MPa,刀具刀尖半径 =3mm, Ra=3.2μm,铣削长度为1000mm,机床类型为VMC-855加工中心。
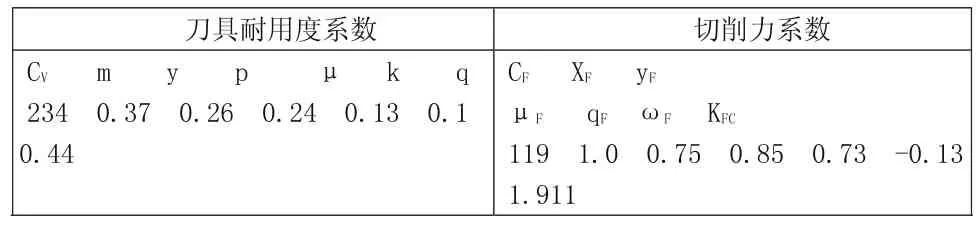
表1 设计参数

图1 优化结果图形表示

图2 求解结果
可以看出,铣削速度为60m/min,每齿进给量0.26214mm/Z。
5 结论
运用遗传算法求解非线性问题,具有收敛速度快、鲁棒性好等特点,在经验值和具体的实际生产加工条件基础上综合考虑得出优化值,从而避免选择参数过于保守不能充分利用机床的效能,具有一定的科学依据,在实际应用中具有指导意义。
[1] 王爱玲,李梦群,冯裕强.数控加工理论与实用技术[M].北京:机械工业出版社,2009.
[2] 原思聪.MATLAB语言及机械工程应用[M].北京:机械工业出版社,2008.
[3] 艾兴,肖诗纲.切削用量简明手册[M].北京:机械工业出版社,1994.
[4] 雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[5] 北京市金属切削理论与实践编委会.金属切削理论与实践中册[M].北京:北京出版社.
[6] 韩荣第,周明,孙玉洁.金属切削原理与刀具[M].哈尔滨:哈尔滨工业大学出版社,2004.
